T15967. Check that all A precedes B

Title Description: given the string \ (s \) containing only a and b, judge whether all \ (a \) are in front of \ (b \)

Idea: simulate according to the meaning of the topic

Time complexity: \ (O(n) \)

Reference code:

class Solution {
public:
    bool checkString(string s) {
        int n = s.size();
        s = 'a' + s;
        for(int i = 1 ; i <= n ; ++i)
            if(s[i] == 'a' && s[i - 1] == 'b') return false;
        return true;
    }
};

T25968. Number of laser beams in banks

Topic Description: give you a two-dimensional matrix. Each row may contain transmitters. Each transmitter can connect with all transmitters in adjacent rows. Ask how many lines can be connected at most. The meaning of adjacency here can be seen in the example below:

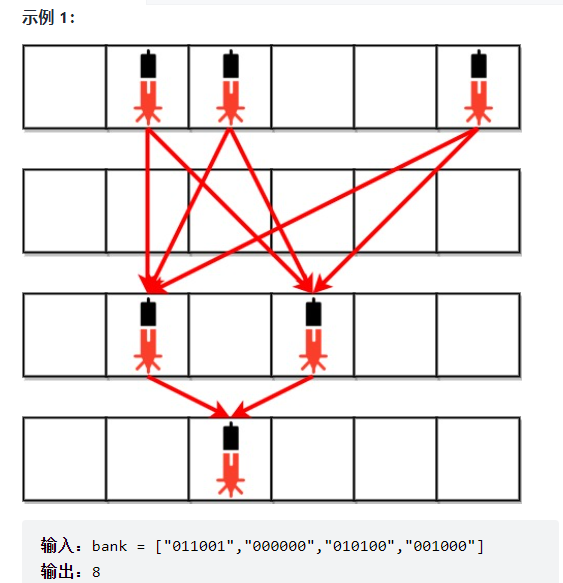
Idea: simulate according to the meaning of the topic

Time complexity: \ (O(n^2) \)

Reference code:

class Solution {
public:
    int numberOfBeams(vector<string>& bank) {
        int res = 0;
        int n = bank.size() , m = bank[0].size();
        for(int i = 0 ; i < n ; ++i){
            int cnt = 0;
            for(auto c : bank[i])  cnt += c =='1';
            if(!cnt) continue;
            for(int j = i + 1 ;  j < n ; ++j){
                int ct = 0;
                for(auto c : bank[j]) ct += c == '1';
                if(!ct) continue;
                res += ct * cnt;
                i = j - 1;
                break;
            }
        }
        return res;
    }
};

T35969. Destruction of asteroids

Title Description: give you an array \ (Num \) and an initial value \ (mass \), rearrange all prefixes after the array and add whether the initial value is not less than the next number. Assuming that the rearranged array is \ (arr \), the more formal description is:

Idea: for very simple questions, after sorting, judge the prefix sum. Note that the prefix sum of this question will exceed the representation range of int32, so pay attention to open long long or do other operations.

Time complexity: \ (O(nlogn + n) = O(nlogn) \)

Reference code:

class Solution {
public:
    bool asteroidsDestroyed(int mass, vector<int>& nums) {
        sort(nums.begin() , nums.end());
        for(auto num : nums){
            if(num > mass) return false;
            mass += num;
            mass = min(mass , 10000005);
        }
        return true;
    }
};

T45970. Maximum number of employees attending meetings

Title Description: there is a round table and \ (n \) individuals. Everyone wants to be adjacent. Ask how many people you can meet at most.

Idea: first, the constraint relationship is a directed graph. You can guess that you need to find the largest ring of the directed graph first. Consider using topological sorting to mark the non ring part, and then use dfs to find the size of the ring and then get the maximum value. However, this is not enough. For binary rings, there are the following situations, so you need to record the maximum depth of each point during topological sorting, The subscript of each ring is stored, and the binary ring is specially treated at the end.

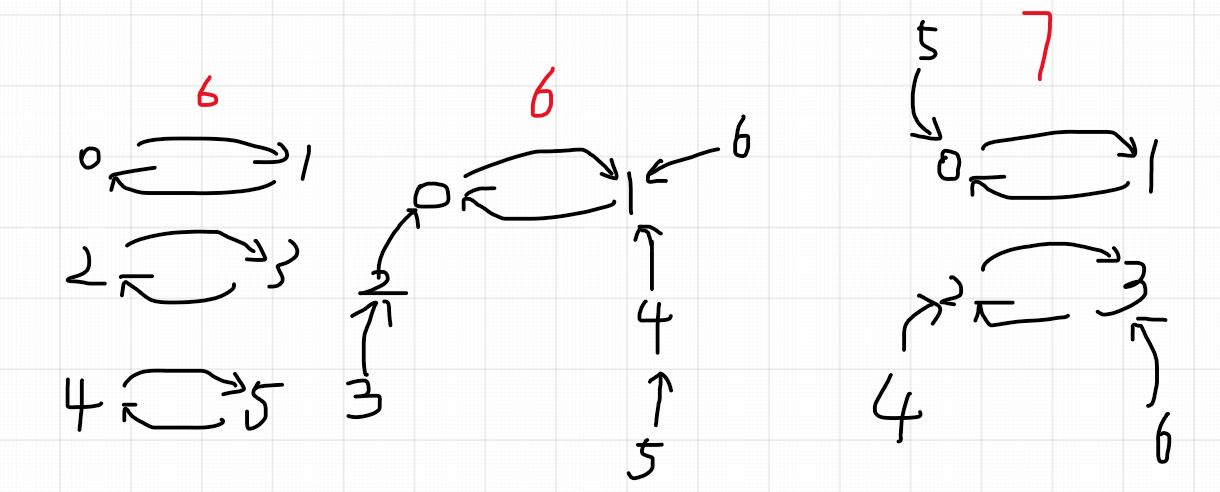
Time complexity: \ (O(n) \)

Reference code:

class Solution {
public:
    int maximumInvitations(vector<int>& fa) {
        int n = fa.size();
        vector<int>income(n , 0);
        vector<vector<int>>g(n , vector<int>(2 , 0));
        for(int i = 0 ; i < n ; ++i){
            income[fa[i]]++;
        }
        vector<bool> vis(n , false);
        vector<int> dep(n , 0);
        queue<int>q;
        for(int i = 0 ; i < n ; ++i){
            if(income[i] != 0) continue;
            g[i][1] = 1;
            q.push(i);
        }
        while(!q.empty()){
            int u = q.front();
            q.pop();
            vis[u] = true;
            income[fa[u]]--;
            dep[fa[u]] = max(dep[fa[u]] , dep[u] + 1);
            if(income[fa[u]] == 0) q.push(fa[u]);
        }
        int res = 0;
       vector<vector<int>>graph(n);
        auto dfs = [&](auto f , int u , int cnt , int fl)->void{
            if(!vis[u]){
                vis[u] = true;
                graph[fl].push_back(u);
                f(f , fa[u] , cnt + 1 , fl);
            }
            res = max(res , cnt);
            return ;
        };
        int idx = 0;
        for(int i = 0 ; i < n ; ++i)
            if(!vis[i]){
                dfs(dfs , i , 0 , idx++);
            }
        int ct = 0;
        for(int i = 0 ; graph[i].size() > 0 ; ++i){
            if(graph[i].size() > 2) continue;
            int u = graph[i][0] , v = graph[i][1];
            ct += 2 + dep[u] + dep[v];
        }
        res = max(res , ct);
        return res;
    }
};