Author: fredalxin
Address: https://fredal.xin/netflix-concuurency-limits

As one of the means to deal with high concurrency, current limiting is not a new topic. From Ratelimiter of Guava to Hystrix and Sentinel can be used as current limiting tools.

Adaptive current limiting

In general, it is often necessary to specify a fixed value (qps) as the threshold of current limit switch. This value is determined by experience and obtained by a large number of test data. However, this threshold may become less appropriate after traffic surge, automatic system scaling, or so and so commit a piece of toxic code. And the general business party is not able to correctly evaluate its own capacity to set an appropriate current limiting threshold.

At this time, adaptive current limiting is to solve this problem. The current limiting threshold does not need to be specified manually, nor does it need to estimate the capacity of the system, and the threshold can change with the change of relevant indicators of the system.

The adaptive current limiting algorithm draws lessons from the TCP congestion algorithm, estimates the current limiting threshold according to various indicators, and adjusts it continuously. The results obtained are as follows:

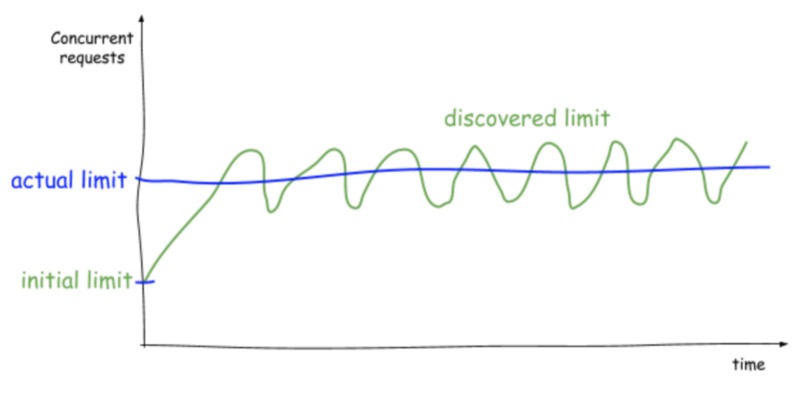As can be seen from the figure, first send the request with a reduced initial concurrency value, and detect higher concurrency of the system by increasing the current limiting window. Once the delay increases to a certain extent, it will return to a smaller current limiting window. Continuously detect the concurrency limit in a circular way, resulting in a sawtooth like time relationship function.

TCP Vegas

vegas is a congestion control algorithm that actively adjusts cwnd. It mainly sets two thresholds, alpha and beta, and then adjusts cwnd by calculating the difference diff between the target rate and the actual rate, and then comparing the relationship between the difference diff and alpha and beta. The pseudo code is as follows:

diff = cwnd*(1-baseRTT/RTT)
if (diff < alpha)
set: cwnd = cwnd + 1 
else if (diff >= beta)
set: cwnd = cwnd - 1
else
set: cwnd = cwnd

Where baseRTT refers to the minimum round-trip time measured, RTT refers to the currently measured round-trip time, and cwnd refers to the current TCP window size. Usually in TCP, alpha is set to 2-3 and beta is set to 4-6. In this way, cwnd is kept in a balanced state.

netflix-concuurency-limits

Containment limits is an adaptive flow limiting component launched by netflix. It draws lessons from the TCP related congestion control algorithm. It mainly adjusts the flow limiting window dynamically according to the request delay and the queue length directly affected by it.

alpha , beta & threshold

The vegas algorithm is implemented in the VegasLimit class. Let's first look at the initialization related codes:

private int initialLimit = 20;
private int maxConcurrency = 1000;
private MetricRegistry registry = EmptyMetricRegistry.INSTANCE;
private double smoothing = 1.0;

private Function<Integer, Integer> alphaFunc = (limit) -> 3 * LOG10.apply(limit.intValue());
private Function<Integer, Integer> betaFunc = (limit) -> 6 * LOG10.apply(limit.intValue());
private Function<Integer, Integer> thresholdFunc = (limit) -> LOG10.apply(limit.intValue());
private Function<Double, Double> increaseFunc = (limit) -> limit + LOG10.apply(limit.intValue());
private Function<Double, Double> decreaseFunc = (limit) -> limit - LOG10.apply(limit.intValue());

Here, we first define an initialization value initialLimit of 20 and a maximum value of maxConcurrency1000. The second is the three threshold functions alpha func, beta func and threshold func. Finally, there are two increase and decrease functions, increaseFunc and decreaseFunc. All functions operate based on the current concurrent value limit.

1. Alpha func can be compared with alpha in vegas algorithm. The implementation here is 3*log limit. When the limit value increases from the initial 20 to the maximum 1000, the corresponding alpha increases from 3.9 to 9.
2. Beta func can be compared to beta in vegas algorithm. The implementation here is 6*log limit. When the limit value increases from the initial 20 to the maximum 1000, the corresponding alpha increases from 7.8 to 18.
3. thresholdFunc is a new function, which represents a relatively initial threshold. When it is less than this value, limit will adopt a more radical incremental algorithm. The implementation here is twice the log limit. When the mit value increases from the initial 20 to the maximum 1000, the corresponding alpha increases from 1.3 to 3.

These three function values can be considered to determine the four interval ranges of the dynamic adjustment function. When the variable queueSize = limit × (1 − RTTnoLoad/RTTactual) apply different adjustment functions when falling into these four intervals.

Variable queueSize

The variable is queueSize and the calculation method is limit × In fact, you can understand why RT1 is so simple.

We think of the process of the system processing the request as a water pipe. The incoming request is to fill the water pipe. When the system processing is smooth, the request does not need to queue up and directly passes through the water pipe. The RT of the request is the shortest, that is, RTTnoLoad;

On the contrary, when requests are stacked, the time for processing requests will change to: queuing time + shortest processing time, that is, RTTactual = inQueueTime + RTTnoLoad. Obviously, the queue length of queuing is the total queuing time / processing time of each request and queueSize = (limit * inQueueTime) / (inQueueTime + RTTnoLoad) = limit × (1 − RTTnoLoad/RTTactual). Another example is chestnuts, because assuming that the current delay is the best delay, there is no need to queue, that is, queueSize=0. Assuming that the current delay is twice the optimal delay, it can be considered that the processing capacity is halved, half of 100 traffic will come in, that is, 50 requests are queued, and queueSize= 100 * (1 − 1 / 2) = 50.

Dynamic adjustment function

The most important adjustment functions are increasing function and decreasing function. It is known from the initialization code that the increment function increaseFunc is implemented as limit+log limit, and the decreaseFunc function is implemented as limit log limit. Relatively speaking, the increase and decrease are relatively conservative.

Let's take a look at the relevant codes that apply the dynamic adjustment function:

private int updateEstimatedLimit(long rtt, int inflight, boolean didDrop) {
    final int queueSize = (int) Math.ceil(estimatedLimit * (1 - (double)rtt_noload / rtt));

    double newLimit;
    // Treat any drop (i.e timeout) as needing to reduce the limit
    // If an error is found, apply the subtraction function decreaseFunc directly
    if (didDrop) {
        newLimit = decreaseFunc.apply(estimatedLimit);
        // Prevent upward drift if not close to the limit
    } else if (inflight * 2 < estimatedLimit) {
        return (int)estimatedLimit;
    } else {
        int alpha = alphaFunc.apply((int)estimatedLimit);
        int beta = betaFunc.apply((int)estimatedLimit);
        int threshold = this.thresholdFunc.apply((int)estimatedLimit);

        // Aggressive increase when no queuing
        if (queueSize <= threshold) {
            newLimit = estimatedLimit + beta;
            // Increase the limit if queue is still manageable
        } else if (queueSize < alpha) {
            newLimit = increaseFunc.apply(estimatedLimit);
            // Detecting latency so decrease
        } else if (queueSize > beta) {
            newLimit = decreaseFunc.apply(estimatedLimit);
            // We're within he sweet spot so nothing to do
        } else {
            return (int)estimatedLimit;
        }
    }

    newLimit = Math.max(1, Math.min(maxLimit, newLimit));
    newLimit = (1 - smoothing) * estimatedLimit + smoothing * newLimit;
    if ((int)newLimit != (int)estimatedLimit && LOG.isDebugEnabled()) {
        LOG.debug("New limit={} minRtt={} ms winRtt={} ms queueSize={}",
                  (int)newLimit,
                  TimeUnit.NANOSECONDS.toMicros(rtt_noload) / 1000.0,
                  TimeUnit.NANOSECONDS.toMicros(rtt) / 1000.0,
                  queueSize);
    }
    estimatedLimit = newLimit;
    return (int)estimatedLimit;
}

The dynamic adjustment function rules are as follows:

1. When the variable queuesize < threshold, select the more radical incremental function, newLimit = limit+beta
2. When the variable queuesize < alpha, it is necessary to increase the current limiting window and select the increasing function increaseFunc, that is, newLimit = limit + log limit
3. When the variable queueSize is between alpha and beta, the limit remains unchanged
4. When the variable queueSize is greater than beta, you need to close the current limit window and select the subtraction function decreaseFunc, that is, newLimit = limit - log limit

Smooth decrement smoothingDecrease

Note that you can set the variable smoothing, where the initial value is 1, which means that smooth decrement does not work.

If necessary, it can be set as needed. For example, when smoothing is set to 0.5, the effect is to halve the effect when using the subtraction function decreaseFunc. The implementation method is newLimitAfterSmoothing = 0.5 newLimit + 0.5 limit.

Recent hot article recommendations:

1.600 + Java interview questions and answers (2021 latest edition)

2.Finally got the IntelliJ IDEA activation code through the open source project. It's really fragrant!

3.Ali Mock tools are officially open source and kill all Mock tools on the market!

4.Spring Cloud 2020.0.0 is officially released, a new and subversive version!

5.Java development manual (Songshan version) is the latest release. Download it quickly!

Feel good, don't forget to like + forward!