Recommend a video resource of Gupao College: link: https://pan.baidu.com/s/1SmSzrmfgbm6XgKZO7utKWg Password: e54x
First, I will answer the questions that students didn't add in the previous release "be careful when using HashMap". I'd better say how HashMap solves the problem of dead cycle in JDK8.
The link list part corresponds to the transfer code above:
Node<K,V> loHead = null, loTail = null; Node<K,V> hiHead = null, hiTail = null; Node<K,V> next; do { next = e.next; if ((e.hash & oldCap) == 0) { if (loTail == null) loHead = e; else loTail.next = e; loTail = e; } else { if (hiTail == null) hiHead = e; else hiTail.next = e; hiTail = e; } } while ((e = next) != null); if (loTail != null) { loTail.next = null; newTab[j] = loHead; } if (hiTail != null) { hiTail.next = null; newTab[j + oldCap] = hiHead; }
Since the capacity expansion is carried out by twice, i.e. n is expanded to N + N, there will be low-level Part 0 - (N-1) and high-level part N - (2N-1), so it is divided into low head (low head) and high head (high head).
Through the above analysis, it is not difficult to find that the generation of the cycle is because the order of the new chain list is completely opposite to that of the old chain list, so as long as the new chain is built according to the original order, the cycle will not be generated.
JDK8 uses head and tail to ensure the order of the linked list is the same as before, so no circular reference will be generated.
Disadvantages of traditional HashMap
Before JDK 1.8, the implementation of HashMap was array + linked list. Even if the hash function is good enough, it is difficult to achieve even distribution of elements.
When a large number of elements in a HashMap are stored in the same bucket, there is a long chain table under the bucket. At this time, HashMap is equivalent to a single chain table. If a single chain table has n elements, the time complexity of traversal is O(n), completely losing its advantages.
In order to solve this problem, red black tree (O(logn) is introduced in JDK 1.8 to optimize this problem.
New data structure - red black tree
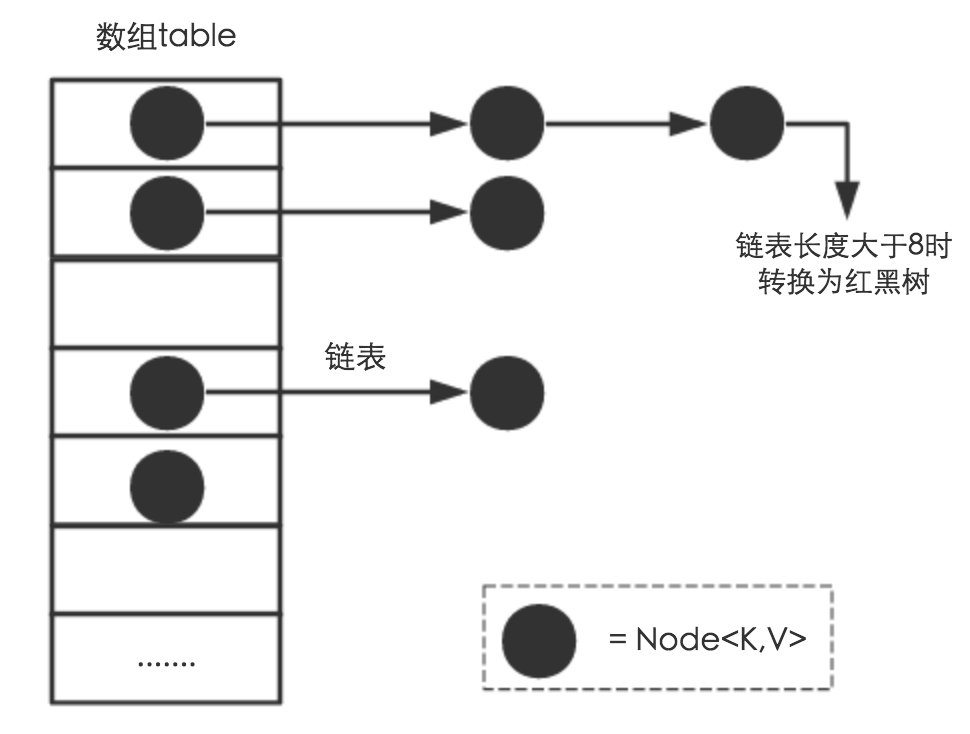
In addition to linked list nodes in HashMap in JDK 1.8:
static class Node implements Map.Entry { //Hash value is the location final int hash; //key final K key; //value V value; //Pointer to the next point Node next; //... }
There is another kind of node: TreeNode, which is newly added in 1.8. It belongs to the red black tree in the data structure Click here to learn about the red black tree):
static final class TreeNode extends LinkedHashMap.Entry { TreeNode parent; // red-black tree links TreeNode left; TreeNode right; TreeNode prev; // needed to unlink next upon deletion boolean red; }
You can see that it is a red and black tree node, with a father, a left and right child, a node of the previous element, and a color value.
In addition, because it inherits from LinkedHashMap.Entry and LinkedHashMap.Entry inherits from HashMap.Node, there are six additional properties:
//Inherited from LinkedHashMap.Entry Entry before, after; //Of HashMap.Node final int hash; final K key; V value; Node next;
Three key parameters of red black tree
There are three key parameters about red black tree in HashMap:
- TREEIFY_THRESHOLD
- UNTREEIFY_THRESHOLD
- MIN_TREEIFY_CAPACITY
The values and functions are as follows:
//Tree threshold of a bucket //When the number of elements in the bucket exceeds this value, you need to replace the linked list node with a red black tree node //This value must be 8, otherwise frequent conversion efficiency is not high static final int TREEIFY_THRESHOLD = 8; //Restore threshold of a tree's linked list //When the capacity is expanded, if the number of elements in the bucket is less than this value, the tree shaped bucket elements will be restored (cut) into a linked list structure //This value should be smaller than the one above, at least 6, to avoid frequent conversion static final int UNTREEIFY_THRESHOLD = 6; //Minimum tree capacity of hash table //When the capacity in the hash table is greater than this value, the buckets in the table can be treelized //Otherwise, if there are too many elements in the barrel, it will expand capacity, rather than tree shape //In order to avoid the conflict of expansion and tree selection, this value cannot be less than 4 * treeify? Treehold static final int MIN_TREEIFY_CAPACITY = 64;
New operation: treeifyBin()
stay Java In 8, if the number of elements in a bucket exceeds treeify? Treehold (the default is 8), the red black tree is used to replace the linked list to improve the speed.
The alternative is treeifyBin(), which is treelification.
//Replace all linked list nodes in the bucket with red black tree nodes final void treeifyBin(Node[] tab, int hash) { int n, index; Node e; //If the current hash table is empty, or the number of elements in the hash table is less than the threshold value for tree formation (64 by default), create / expand if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY) resize(); else if ((e = tab[index = (n - 1) & hash]) != null) { //If the number of elements in the hash table exceeds the tree threshold, tree // e is the link list node in the bucket in the hash table, starting from the first one TreeNode hd = null, tl = null; //The head and tail nodes of the red black tree do { //Create a new tree node with the same content as the current linked list node e TreeNode p = replacementTreeNode(e, null); if (tl == null) //Determine tree head node hd = p; else { p.prev = tl; tl.next = p; } tl = p; } while ((e = e.next) != null); //Let the first element of the bucket point to the newly created red black tree header node. In the future, the element in the bucket is the red black tree instead of the linked list if ((tab[index] = hd) != null) hd.treeify(tab); } } TreeNode replacementTreeNode(Node p, Node next) { return new TreeNode<>(p.hash, p.key, p.value, next); }
The above operations do these things:
- Determine whether to expand or tree based on the number of elements in the hash table
- If it's treelization
- Traverse the elements in the bucket, create the same number of tree nodes, copy the content, and establish a connection
- Then let the first element of the bucket point to the new tree head node, and replace the bucket's chain content with tree content
But we found that the previous operation did not set the color value of the red black tree, and now we can only get a binary tree. Finally, we call the tree node hd.treeify(tab) method to shape the red black tree.
final void treeify(Node[] tab) { TreeNode root = null; for (TreeNode x = this, next; x != null; x = next) { next = (TreeNode)x.next; x.left = x.right = null; if (root == null) { //Enter the cycle for the first time, confirm the head node, which is black x.parent = null; x.red = false; root = x; } else { //After that, enter the logic of looping. x points to a node in the tree K k = x.key; int h = x.hash; Class kc = null; //Another loop starts from the root node, traverses all nodes and compares them with the current node x, adjusts the position, which is a bit like bubble sorting for (TreeNode p = root;;) { int dir, ph; //This dir K pk = p.key; if ((ph = p.hash) > h) //When the hash value of the comparison node is larger than x, dir is - 1 dir = -1; else if (ph < h) //Hash value ratio x hour dir is 1 dir = 1; else if ((kc == null && (kc = comparableClassFor(k)) == null) || (dir = compareComparables(kc, k, pk)) == 0) // If comparing the hash value of a node, x dir = tieBreakOrder(k, pk); //Make the current node the father of x //If the hash value of the current comparison node is larger than x, X is the left child, otherwise x is the right child TreeNode xp = p; if ((p = (dir <= 0) ? p.left : p.right) == null) { x.parent = xp; if (dir <= 0) xp.left = x; else xp.right = x; root = balanceInsertion(root, x); break; } } } } moveRootToFront(tab, root); }
As you can see, when turning a binary tree into a red black tree, you need to ensure order. There is a double cycle here. Compare the hash values of all nodes in the tree with that of the current node (if the hash values are equal, the comparison key is used, and here it is not completely ordered). Then determine the location of the tree species according to the comparison results.
New operation: add element putTreeVal() in red black tree
The above describes how to change the linked list structure in a bucket into a red black tree structure.
When adding, if a bucket already has a red black tree structure, the red black tree's add element method putTreeVal() should be called.
final TreeNode putTreeVal(HashMap map, Node[] tab, int h, K k, V v) { Class kc = null; boolean searched = false; TreeNode root = (parent != null) ? root() : this; //Each time an element is added, it is traversed from the root node and compared with the hash value for (TreeNode p = root;;) { int dir, ph; K pk; if ((ph = p.hash) > h) dir = -1; else if (ph < h) dir = 1; else if ((pk = p.key) == k || (k != null && k.equals(pk))) //If the hash value, key and the one to be added of the current node are the same, the current node will be returned return p; else if ((kc == null && (kc = comparableClassFor(k)) == null) || (dir = compareComparables(kc, k, pk)) == 0) { //If the hash values of the current node and the node to be added are the same, but the keys of the two nodes are not the same class, you have to compare the left and right children one by one if (!searched) { TreeNode q, ch; searched = true; if (((ch = p.left) != null && (q = ch.find(h, k, kc)) != null) || ((ch = p.right) != null && (q = ch.find(h, k, kc)) != null)) //If you can find the node you want to add from the subtree of ch, you can directly return return q; } //The hash value is equal, but the key cannot be compared, so we have to give a result in a special way dir = tieBreakOrder(k, pk); } //After the previous calculation, a size relationship between the current node and the node to be inserted is obtained //If the node to be inserted is smaller than the current node, it will be inserted into the left subtree, and if it is larger, it will be inserted into the right subtree TreeNode xp = p; //Here is a judgment. If the current node has no left or right child, it can be inserted. Otherwise, it will enter the next cycle if ((p = (dir <= 0) ? p.left : p.right) == null) { Node xpn = xp.next; TreeNode x = map.newTreeNode(h, k, v, xpn); if (dir <= 0) xp.left = x; else xp.right = x; xp.next = x; x.parent = x.prev = xp; if (xpn != null) ((TreeNode)xpn).prev = x; //Necessary balance adjustment operation after inserting elements in red black tree moveRootToFront(tab, balanceInsertion(root, x)); return null; } } } //This method is used to compare the hash values of a and b according to the address of two references when they are the same but cannot be compared //The source code annotation also says that complete order is not required in this tree, as long as the same rules are used to maintain balance when inserting static int tieBreakOrder(Object a, Object b) { int d; if (a == null || b == null || (d = a.getClass().getName(). compareTo(b.getClass().getName())) == 0) d = (System.identityHashCode(a) <= System.identityHashCode(b) ? -1 : 1); return d; }
From the above code, we can know that when adding a new node n to the red black tree in the HashMap, there are the following operations:
- Start from the root node to traverse the element P in the current red black tree, and compare the hash values of n and p;
- If the hash values are the same and the keys are the same, it is judged that this element already exists (it is not clear why the ratio is not correct here);
- If the hash value uses other information, such as the reference address, to give a rough comparison result, you can see that the comparison of red black trees is not very accurate. The notes also say that only to ensure a relative balance can be achieved;
- Finally, after the hash value comparison results are obtained, if the current node p has no left child or right child, it can be inserted, otherwise it will enter the next cycle;
- After the element is inserted, the routine balance adjustment of the red black tree is also required, and the leading position of the root node is ensured.
New operation: find element getTreeNode() in red black tree
The search method of HashMap is get():
public V get(Object key) { Node e; return (e = getNode(hash(key), key)) == null ? null : e.value; }
After calculating the hash value of the specified key, it calls the internal method getNode();
final Node getNode(int hash, Object key) { Node[] tab; Node first, e; int n; K k; if ((tab = table) != null && (n = tab.length) > 0 && (first = tab[(n - 1) & hash]) != null) { if (first.hash == hash && // always check first node ((k = first.key) == key || (key != null && key.equals(k)))) return first; if ((e = first.next) != null) { if (first instanceof TreeNode) return ((TreeNode)first).getTreeNode(hash, key); do { if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) return e; } while ((e = e.next) != null); } } return null; }
This getNode() method is to get the head node of the bucket where the key is located according to the number of hash table elements and the hash value (the formula used is (n - 1) & hash). If the head node happens to be a red black tree node, call the getTreeNode() method of the red black tree node, otherwise traverse the linked list node.
final TreeNode getTreeNode(int h, Object k) { return ((parent != null) ? root() : this).find(h, k, null); }
The getTreeNode method enables to find by calling the find() method of the tree node:
//Search from root node according to hash value and key final TreeNode find(int h, Object k, Class kc) { TreeNode p = this; do { int ph, dir; K pk; TreeNode pl = p.left, pr = p.right, q; if ((ph = p.hash) > h) p = pl; else if (ph < h) p = pr; else if ((pk = p.key) == k || (k != null && k.equals(pk))) return p; else if (pl == null) p = pr; else if (pr == null) p = pl; else if ((kc != null || (kc = comparableClassFor(k)) != null) && (dir = compareComparables(kc, k, pk)) != 0) p = (dir < 0) ? pl : pr; else if ((q = pr.find(h, k, kc)) != null) return q; else p = pl; } while (p != null); return null; }
Since the tree has been guaranteed to be orderly when it was added before, the search is basically a half search with high efficiency.
Here is the same as when inserting. If the hash value of the comparison node is equal to the hash value to be searched, it will be judged whether the key is equal. If it is equal, it will be returned directly (there is no judgment value). If it is not equal, it will be recursively searched from the subtree.
New operation: tree structure pruning split()
In HashMap, the resize() method is used to initialize or expand the hash table. When expanding, if the element structure in the current bucket is a red black tree and the number of elements is less than the threshold value of list restore untreeify ﹐ threehold (default is 6), the tree structure in the bucket will be reduced or directly restored (cut) to the list structure, and split() is called:
//Parameter introduction //tab represents the hash table that holds the bucket head node //index indicates where to start trimming //Bits to trim (hash value) final void split(HashMap map, Node[] tab, int index, int bit) { TreeNode b = this; // Relink into lo and hi lists, preserving order TreeNode loHead = null, loTail = null; TreeNode hiHead = null, hiTail = null; int lc = 0, hc = 0; for (TreeNode e = b, next; e != null; e = next) { next = (TreeNode)e.next; e.next = null; //If the last bit of the current node hash value is equal to the bit value to be trimmed if ((e.hash & bit) == 0) { //Put the current node in the lXXX tree if ((e.prev = loTail) == null) loHead = e; else loTail.next = e; //Then loTail records e loTail = e; //Record the number of nodes in the lXXX tree ++lc; } else { //If the last bit of the current node hash value is not to be trimmed //Put the current node in the hXXX tree if ((e.prev = hiTail) == null) hiHead = e; else hiTail.next = e; hiTail = e; //Record the number of nodes in the hXXX tree ++hc; } } if (loHead != null) { //If the number of lXXX trees is less than 6, leave the branches, leaves and leaves of lXXX trees empty and become a single node //Then let the nodes in the bucket after the index position to be restored become lXXX nodes of the linked list //This element is followed by a linked list structure if (lc <= UNTREEIFY_THRESHOLD) tab[index] = loHead.untreeify(map); else { //Otherwise, let the node in the index position point to the lXXX tree, which has been pruned and has fewer elements tab[index] = loHead; if (hiHead != null) // (else is already treeified) loHead.treeify(tab); } } if (hiHead != null) { //Similarly, let the element after the specified position index + bit //Point to hXXX to restore to linked list or pruned tree if (hc <= UNTREEIFY_THRESHOLD) tab[index + bit] = hiHead.untreeify(map); else { tab[index + bit] = hiHead; if (loHead != null) hiHead.treeify(tab); } } }
From the above code, it can be seen that the pruning of the red black tree node during the expansion of HashMap is mainly divided into two parts. First, it is classified, and then it is determined whether to restore to the linked list or to simplify the elements and still retain the red black tree structure according to the number of elements.
1. classification
Specify the location and range. If the element in the specified location (hash & bit) = = 0, put it in the lXXX tree. If it is not equal, put it in the hXXX tree.
2. Determine the processing according to the number of elements
When the number of elements (i.e. lXXX tree) meets the requirements, it will be restored to a linked list when the number of elements is less than 6, and finally the pruned pain tab[index] in the hash table will point to the lXXX tree; when the number of elements is greater than 6, it will still use the red black tree, just pruning the lower branches and leaves;
The elements that do not meet the requirements (i.e. hXXX tree) are also operated in the same way, but in the end, they are placed outside the trimming range tab[index + bit].
summary
After JDK 1.8, the methods of adding, deleting, finding and expanding hash tables add a TreeNode node
- When it is added, when the number of linked lists in the bucket exceeds 8, it will be converted into a red black tree;
- When deleting or expanding, if the bucket structure is a red black tree and the number of elements in the tree is too small, it will be pruned or directly restored to the linked list structure;
- Even if the Hashi function is not good, a large number of elements are concentrated in a bucket. Due to the red black tree structure, the performance is not bad.
(image from: tech.meituan.com/java-hashma...)
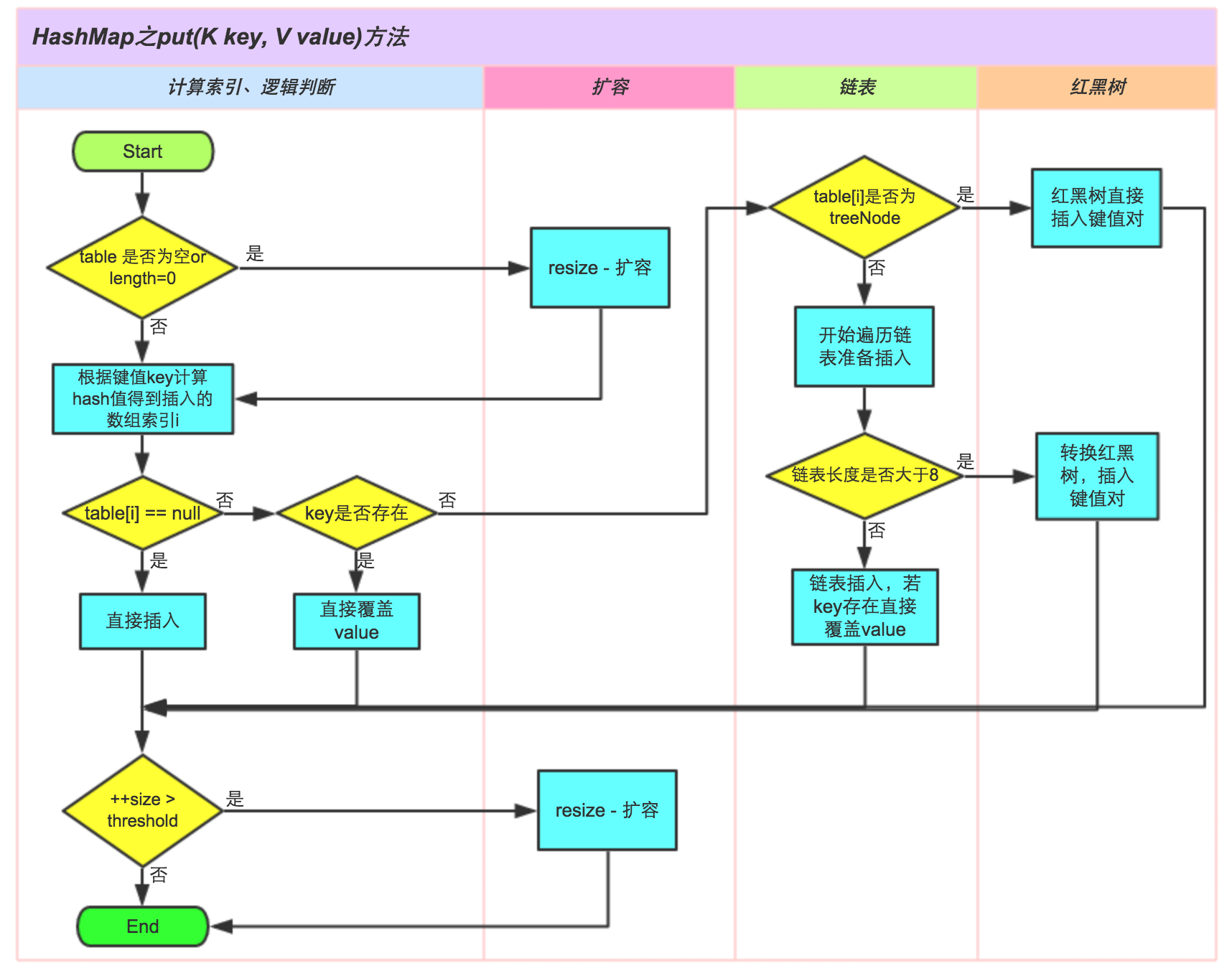
This article analyzes some key methods of TreeNode added by HashMap in JDK 1.8 according to the source code. It can be seen that after 1.8, HashMap combines the advantages of hash table and red black tree. It is not only fast, but also can guarantee performance in extreme cases. The designer is painstaking to see a spot. When can I write this NB The code of!!!
Reference address
- https://cloud.tencent.com/developer/article/1120823
- https://juejin.im/entry/5839ad0661ff4b007ec7cc7a
If you like my article, you can pay attention to the personal subscription number. Welcome to leave a message and communicate at any time.
