
This series will update an algorithm problem every day. If you think the content is helpful to you, please praise it.
1, Title Description
Given n non negative integers to represent the height diagram of each column with width 1, calculate how much rain the columns arranged according to this can receive after rain.
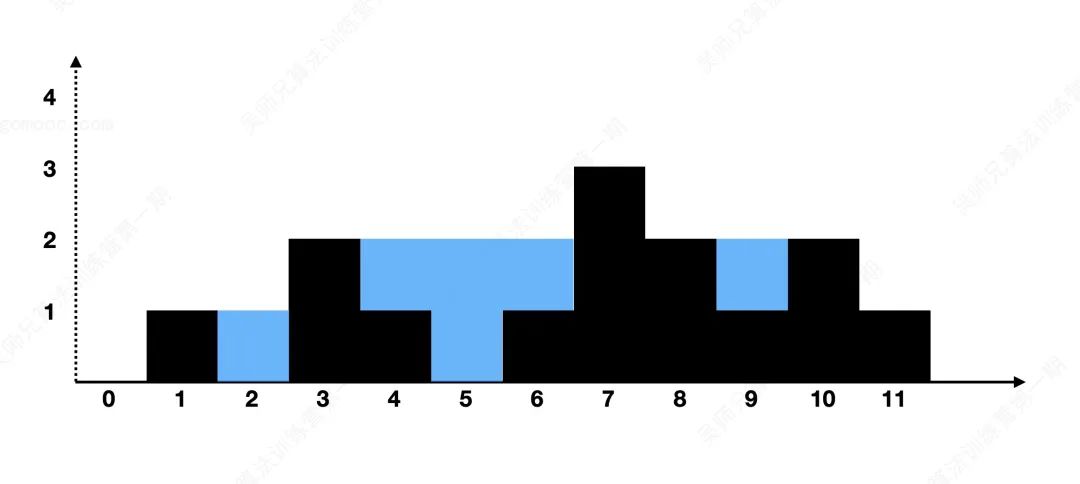
Input: height = [0,1,0,2,1,0,1,3,2,1,2,1] Output: 6 Explanation: the above is composed of an array [0,1,0,2,1,0,1,3,2,1,2,1] In this case, 6 units of rainwater can be connected (the blue part represents rainwater).
2, Topic analysis
We picked up the rain in the direction of the line.
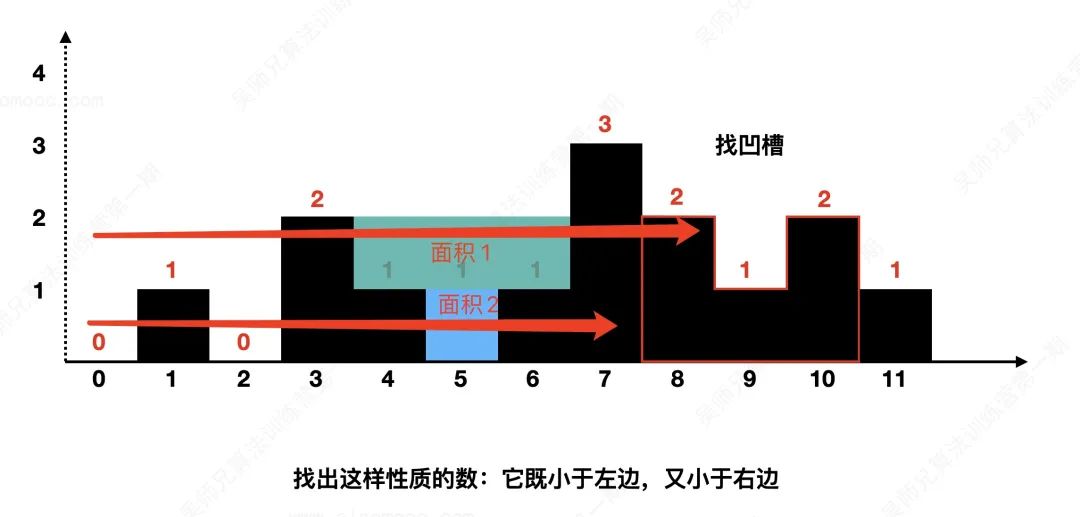
Next, let's look for the groove.
A groove is surrounded by three columns. (for the convenience of description, we regard the column with height 0 as an existing column)
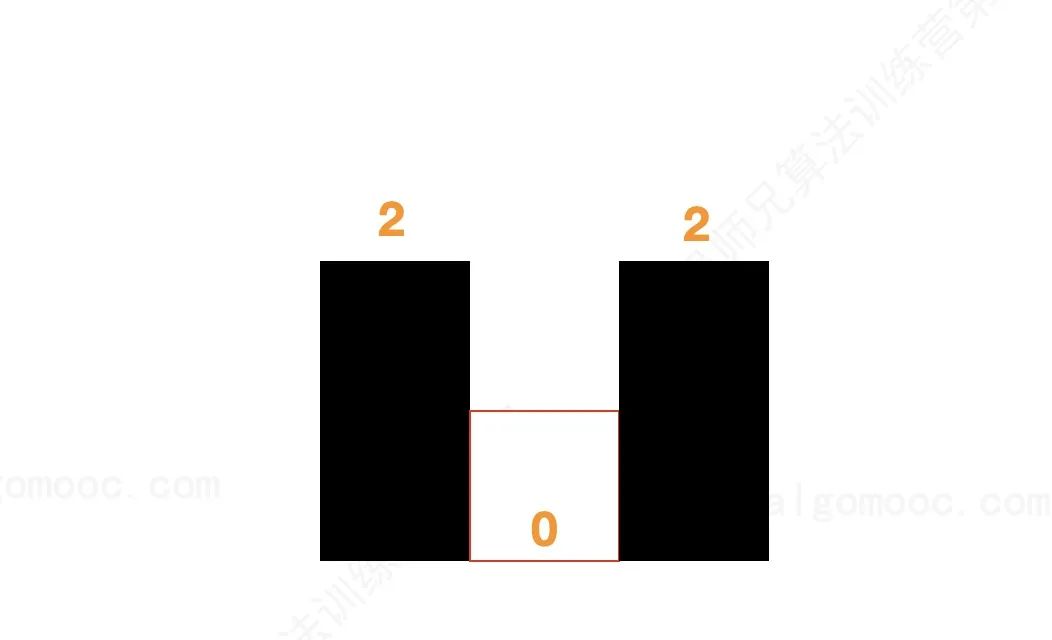
For this groove, its left and bottom are selected from the stack, and its right is determined by the newly added column.
What happens to grooves?
Once the height of the newly added column is greater than the stack top element, it is possible to form a groove!
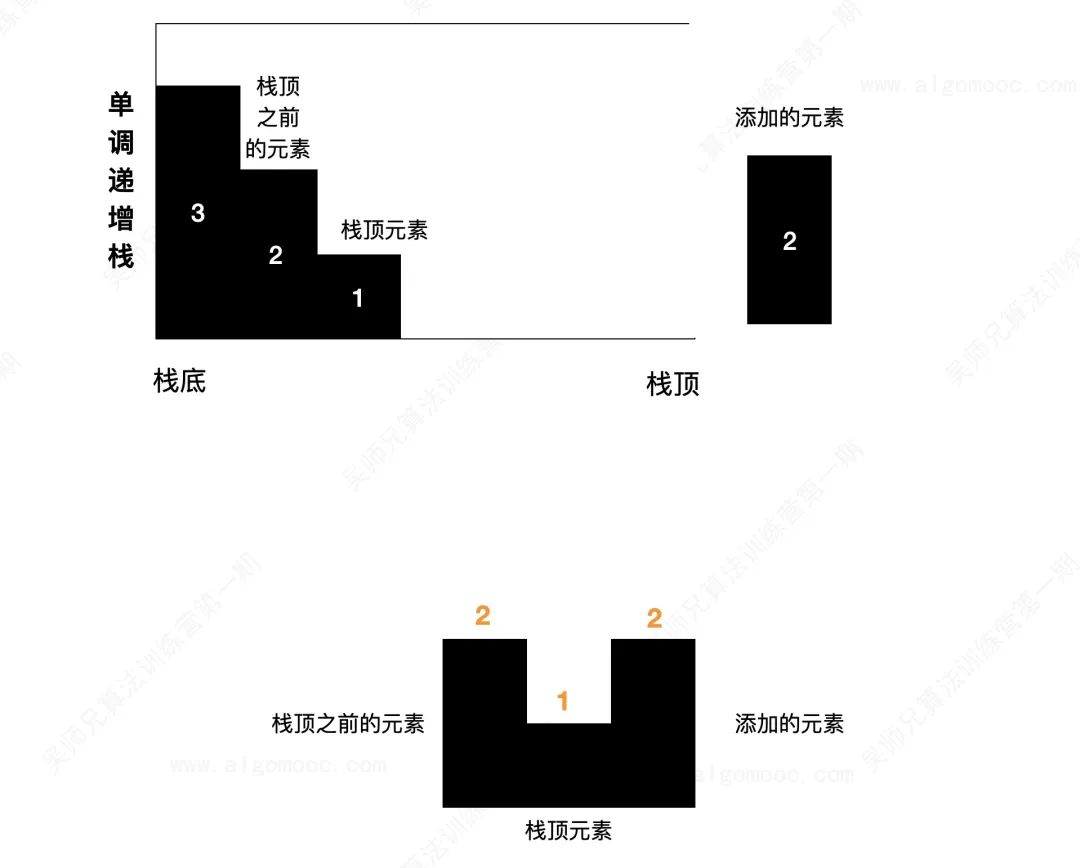
At this time, the top element of the stack is the bottom of the groove. If there is an element before the top element in the stack, the element before the top element is the left side of the groove. At this time, the added element is the right side of the groove.
The reason why it is possible here is that there may be two columns with the same height in the column. Even if the height of the newly added columns is greater than them, they cannot form a groove, or form a groove with an area of 0.
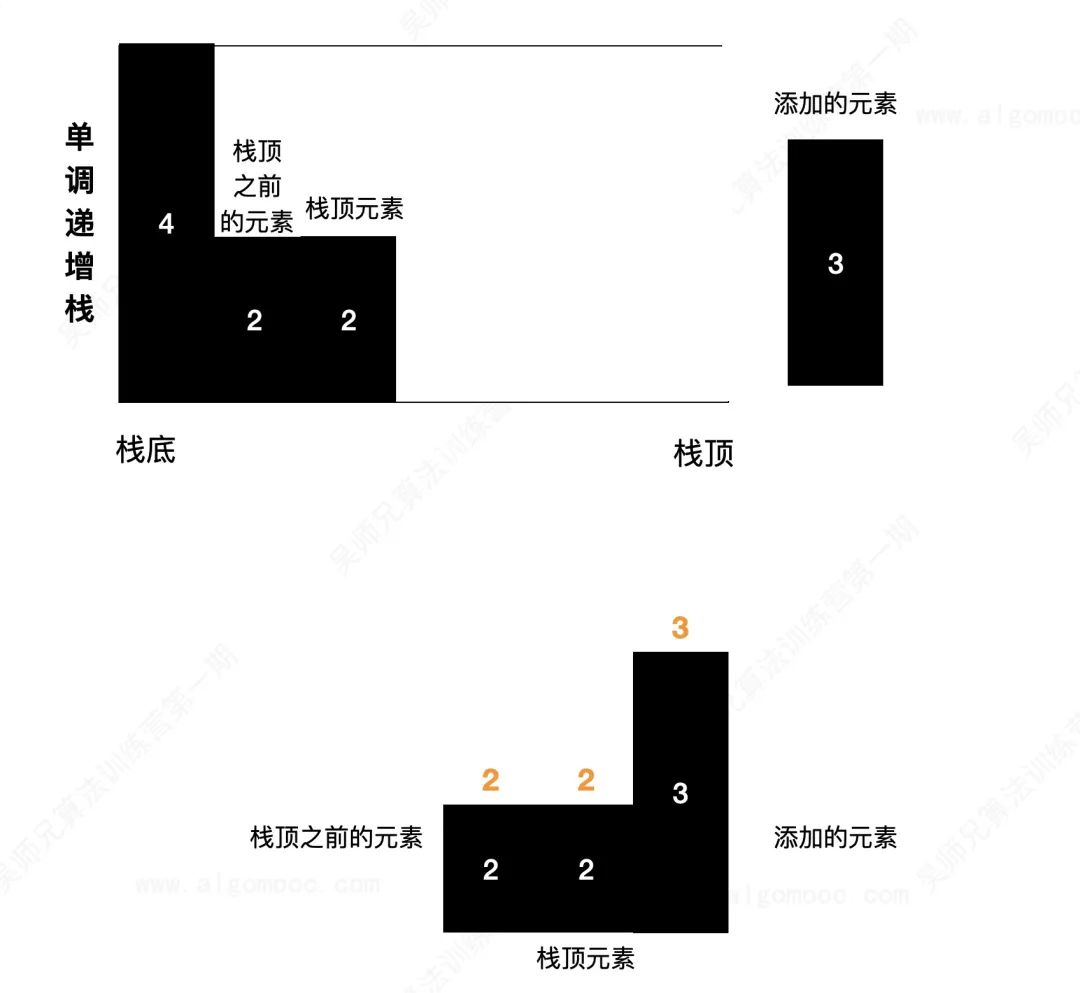
If the height of the newly added column is less than the element at the top of the stack, it must not form a groove with the elements in the current stack, because this is a monotonous stack. The closer the elements inside are to the top of the stack, the smaller the height of the newly added column is. If the height of the newly added column is less than the element at the top of the stack, it must be less than other elements inside. In this case, a groove cannot be enclosed, We will add the current column to our stack and let it wait for the next column together with the columns inside.
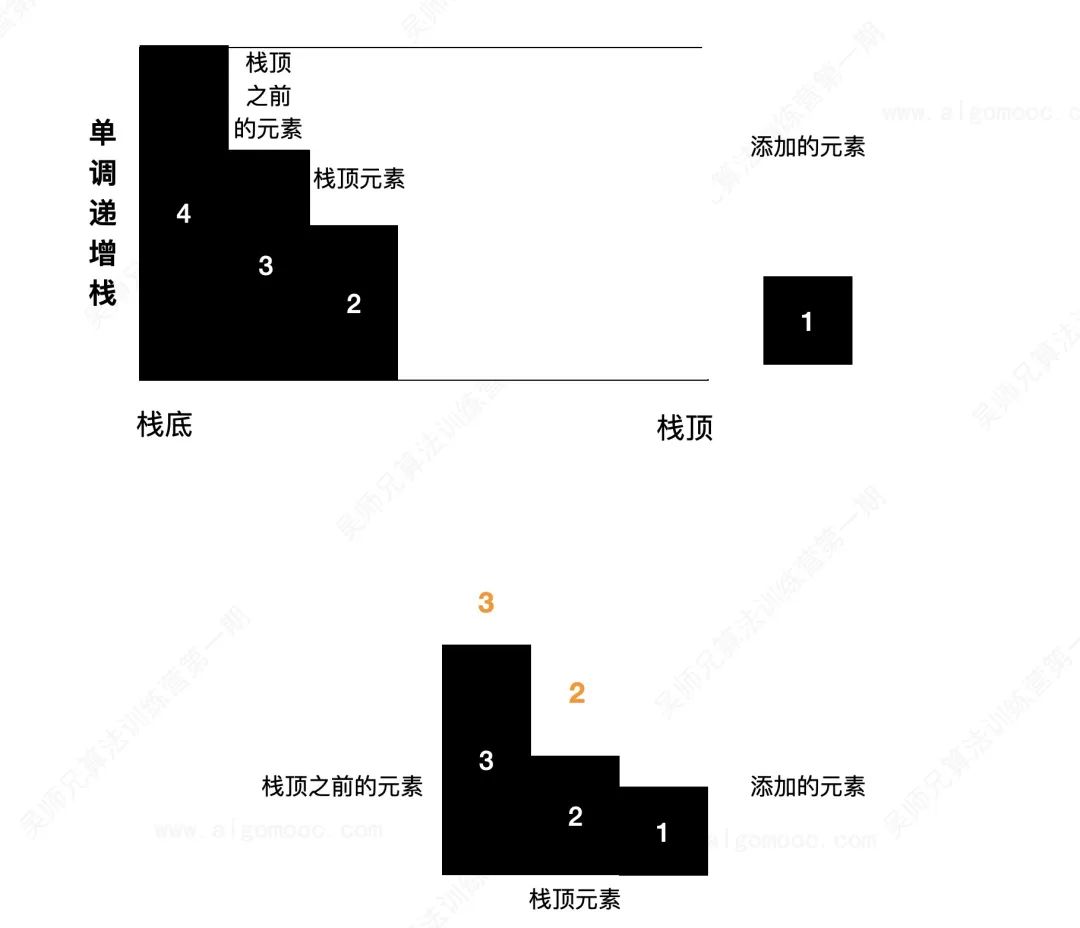
If the height of the newly added column is equal to the top element of the stack, it cannot form a groove. We will add the current column to our stack and let it wait for the next column together with the columns inside.
Once the groove is formed, we calculate its area.
The area is determined by height and width.
The height of the groove is calculated by min (the height of the left side of the groove and the height of the right side of the groove) - the height of the bottom of the groove.
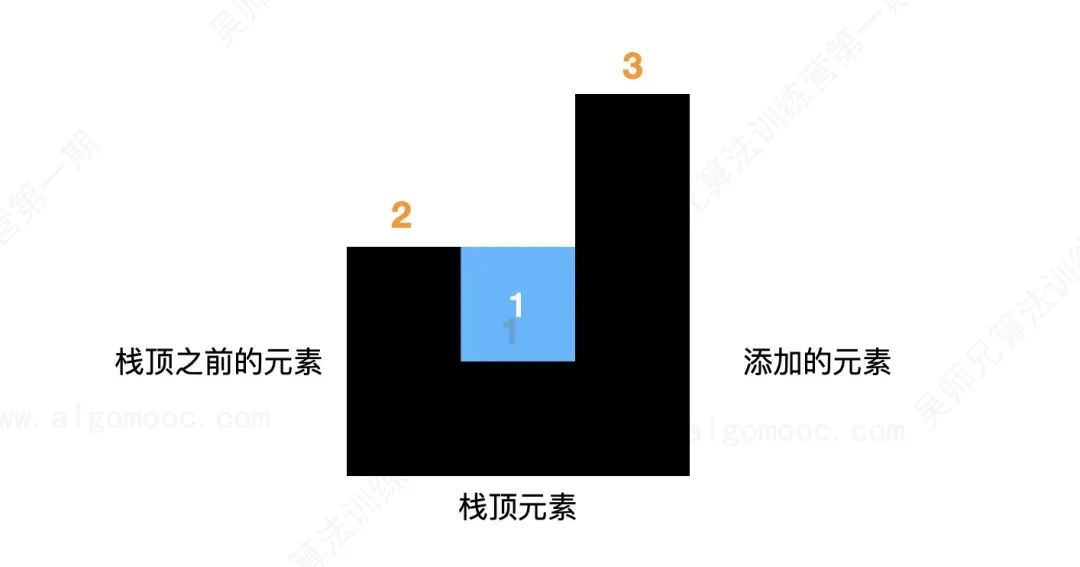
The width of the groove is calculated by the subscript to the right of the groove - the subscript to the left of the groove - 1 (because only the middle width is required).

After calculating the area of a groove, we pop up the top elements of the stack and observe whether the remaining elements in the stack can form a new groove with the newly added elements.
3, Reference code
1. Java code
// Log in to AlgoMooc's official website for more algorithm diagrams
// https://www.algomooc.com
// Author: programmer senior brother Wu
// If you don't understand the code, you must talk to elder martial brother Wu privately
// Connected to rainwater (LeetCode 42): https://leetcode-cn.com/problems/trapping-rain-water/
class Solution {
public int trap(int[] height) {
// Only two columns cannot form a groove, so the area of water is 0
if (height.length <= 2) return 0;
// Build a stack to store the subscript of the corresponding column
// Note: stack stores subscripts instead of heights
Stack<Integer> stack = new Stack<>();
// At first, the area of water was 0
int result = 0;
// Traverse the entire array from scratch
for (int i = 0; i < height.length; i++) {
// If the stack is empty, the current index is directly added to the stack
if(stack.isEmpty()){
// Adds the current index to the stack
stack.push(i);
// Otherwise, there is value in the stack. We need to judge whether the element at this time, the element at the top of the stack and the element before the top of the stack can form a groove
// Case 1: the element at this time is smaller than the element at the top of the stack, and the right side of the groove does not exist, so the groove cannot be formed
}else if (height[i] < height[stack.peek()]) {
// Adds the current index to the stack
stack.push(i);
// Case 2: the element at this time is equal to the element at the top of the stack, and the groove cannot be formed
} if (height[i] == height[stack.peek()]) {
// Adds the current index to the stack
stack.push(i);
// Case 3: the element at this time is larger than the element at the top of the stack, and a groove may be formed
// Note that it is possible to form a groove, because for example, if the element in the stack is 2 or 2 and the element in this case is 3, the groove cannot be formed
} else {
// Since there may be multiple elements in the stack, after removing the top element of the stack, the remaining elements and the elements at this time may also form grooves
// Therefore, we need to constantly compare the elements at this time with the elements at the top of the stack
// When the element at this time is still larger than the element at the top of the stack, we calculate the groove area at this time
// This is done with a while loop
while (!stack.empty() && height[i] > height[stack.peek()]) {
// 1. Get the subscript of the top of the stack, and bottom is the bottom position of the groove
int bottom = stack.peek();
// Push out the stack top element to determine whether the element before the stack top exists, that is, whether the left side of the groove exists
stack.pop();
// 2. If the stack is not empty, there are elements in the stack, that is, there are elements on the left side of the groove
if (!stack.empty()) {
// Height [stack. Peek] on the left side of the groove and height[i] on the right side of the groove
// The minimum value of these two minus the height of the bottom of the groove is the height of the groove
int h = Math.min(height[stack.peek()], height[i]) - height[bottom];
// The width of the groove is equal to the subscript value i on the right side of the groove minus the subscript value stack on the left side of the groove Peek minus 1
int w = i - stack.peek() - 1;
System.out.println("Groove right-->" + i);
System.out.println("Groove left-->" + stack.peek());
System.out.println("Groove height-->" + h);
System.out.println("Groove width-->" + w);
System.out.println("Groove area-->" + h * w);
System.out.println("---------------");
// Add the calculated results to the final results
result += h * w;
}
}
// The situation that the elements in the stack and at this time can form a stack has been determined in the while loop above
// Then, the elements in the stack at this time must not be larger than the elements at this time, so you can add the elements at this time to the stack
stack.push(i);
}
}
// Finally, return the result
return result;
}
}
2. C + + code
// Log in to AlgoMooc's official website for more algorithm diagrams
// https://www.algomooc.com
// Author: programmer senior brother Wu
// If you don't understand the code, you must talk to elder martial brother Wu privately
// Connected to rainwater (LeetCode 42): https://leetcode-cn.com/problems/trapping-rain-water/
class Solution {
public:
int trap(vector<int>& height) {
// Only two columns cannot form a groove, so the area of water is 0
if (height.size() <= 2) return 0;
// Build a stack to store the subscript of the corresponding column
// Note: stk stores subscripts instead of heights
stack<int> stk ;
// At first, the area of water was 0
int result = 0;
// Traverse the entire array from scratch
for (int i = 0; i < height.size(); i++) {
// If the stack is empty, the current index is directly added to the stack
if(stk.empty()){
// Adds the current index to the stack
stk.push(i);
// Otherwise, there is value in the stack. We need to judge whether the element at this time, the element at the top of the stack and the element before the top of the stack can form a groove
// Case 1: the element at this time is smaller than the element at the top of the stack, and the right side of the groove does not exist, so the groove cannot be formed
}else if (height[i] < height[stk.top()]) {
// Adds the current index to the stack
stk.push(i);
// Case 2: the element at this time is equal to the element at the top of the stack, and the groove cannot be formed
} else if (height[i] == height[stk.top()]) {
// Adds the current index to the stack
stk.push(i);
// Case 3: the element at this time is larger than the element at the top of the stack, and a groove may be formed
// Note that it is possible to form a groove, because for example, if the element in the stack is 2 or 2 and the element in this case is 3, the groove cannot be formed
} else {
// Since there may be multiple elements in the stack, after removing the top element of the stack, the remaining elements and the elements at this time may also form grooves
// Therefore, we need to constantly compare the elements at this time with the elements at the top of the stack
// When the element at this time is still larger than the element at the top of the stack, we calculate the groove area at this time
// This is done with a while loop
while (!stk.empty() && height[i] > height[stk.top()]) {
// 1. Get the subscript of the top of the stack, and bottom is the bottom position of the groove
int bottom = stk.top();
// Push out the stack top element to determine whether the element before the stack top exists, that is, whether the left side of the groove exists
stk.pop();
// 2. If the stack is not empty, there are elements in the stack, that is, there are elements on the left side of the groove
if (!stk.empty()) {
// Height [STK. Top] on the left side of the groove and height[i] on the right side of the groove
// The minimum value of these two minus the height of the bottom of the groove is the height of the groove
int h = min(height[stk.top()], height[i]) - height[bottom];
// The width of the groove is equal to the subscript value i on the right side of the groove minus the subscript value stk.top on the left side of the groove minus 1
int w = i - stk.top() - 1;
// Add the calculated results to the final results
result += h * w;
}
}
// The situation that the elements in the stack and at this time can form a stack has been determined in the while loop above
// Then, the elements in the stack at this time must not be larger than the elements at this time, so you can add the elements at this time to the stack
stk.push(i);
}
}
// Finally, return the result
return result;
}
};
3. Python code
# Log in to AlgoMooc's official website for more algorithm diagrams
# https://www.algomooc.com
# Author: programmer senior brother Wu
# If you don't understand the code, you must talk to elder martial brother Wu privately
# Connected to rainwater (LeetCode 42): https://leetcode-cn.com/problems/trapping-rain-water/
class Solution:
def trap(self, height: List[int]) -> int:
# Build a stack to store the subscript of the corresponding column
# stack stores subscripts, not heights
stack = list()
# At first, the area of water was 0
result = 0
# Gets the length of the array
n = len(height)
# Traverse the entire array from scratch
for i, h in enumerate(height):
# If the stack is empty, the current index is directly added to the stack
if not stack :
# Adds the current index to the stack
stack.append(i)
# Otherwise, there is value in the stack. We need to judge whether the element at this time, the element at the top of the stack and the element before the top of the stack can form a groove
# Case 1: the element at this time is smaller than the element at the top of the stack, and the right side of the groove does not exist, so the groove cannot be formed
elif height[i] < height[stack[-1]]:
# Adds the current index to the stack
stack.append(i)
# Case 2: the element at this time is equal to the element at the top of the stack, and the groove cannot be formed
elif height[i] == height[stack[-1]]:
# Adds the current index to the stack
stack.append(i)
# Case 3: the element at this time is larger than the element at the top of the stack, and a groove may be formed
# Note that it is possible to form a groove, because for example, if the element in the stack is 2 or 2 and the element in this case is 3, the groove cannot be formed
else :
# Since there may be multiple elements in the stack, after removing the top element of the stack, the remaining elements and the elements at this time may also form grooves
# Therefore, we need to constantly compare the elements at this time with the elements at the top of the stack
# When the element at this time is still larger than the element at the top of the stack, we calculate the groove area at this time
# This is done with a while loop
while stack and height[i] > height[stack[-1]]:
# 1. Get the subscript of the top of the stack, and bottom is the bottom position of the groove
bottom = stack[-1]
# Push out the stack top element to determine whether the element before the stack top exists, that is, whether the left side of the groove exists
stack.pop()
# 2. If the stack is not empty, there are elements in the stack, that is, there are elements on the left side of the groove
if stack :
# height[stack[-1] on the left side of the groove and height[i] on the right side of the groove
# The minimum value of these two minus the height of the bottom of the groove is the height of the groove
h = min(height[stack[-1]], height[i]) - height[bottom]
# The width of the groove is equal to the subscript value i on the right side of the groove minus the subscript value stack on the left side of the groove Top minus 1
w = i - stack[-1] - 1
# Add the calculated results to the final results
result += h * w
# The situation that the elements in the stack and at this time can form a stack has been determined in the while loop above
# Then, the elements in the stack at this time must not be larger than the elements at this time, so you can add the elements at this time to the stack
stack.append(i)
# Finally, return the result
return result