Why use LRU algorithm? How to implement Java?

Posted by devain on Sun, 19 Dec 2021 19:40:28 +0100

1, Introduction to LRU algorithm

The full name of LRU algorithm is Least Recently Used, that is, check the Least Recently Used data. It is usually used in the memory elimination strategy to move infrequently used data out of memory to make room for "hot data" or new data.

In essence, the algorithm is very simple. It only needs to sort all the data according to the use time, and eliminate the oldest data when it needs to be eliminated.

2, Application of LRU algorithm

LRU algorithm has many applications. Here we extract a typical application from hardware and software to introduce.

1. Linux memory paging

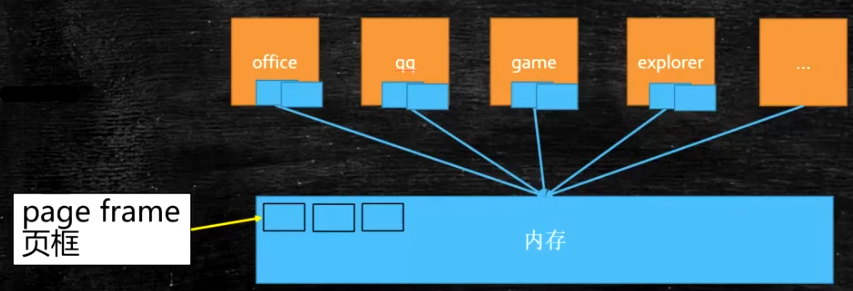
Paging is to solve the problem of insufficient memory. It divides the memory into fixed size page frames (page frame 4K standard pages), divides the programs on the hard disk into 4K size blocks and loads them into the page frame. Whichever block is used later, it will be loaded.

During the loading process, if the memory is full, the least commonly used block will be placed in the swap partition and the latest block will be loaded. Here is the application of LRU algorithm.

2. Redis memory elimination strategy

When Redis has insufficient memory (exceeding the maxmemory limit) to use, it will use the selected memory elimination strategy to eliminate the data.

Relevant LRU policies:

Allkeys LRU: remove the least recently used key;
Volatile LRU: remove the least recently used key in the key space with expiration time set;

LRU bottom layer implementation:

There is a 24bit lru field in the Redis object header to record the heat of the object.
In LRU mode, the LRU field stores the Redis clock server Lruclock – self incrementing integer.
When a key is accessed once, the lru field in its object header will be updated to server lruclock.
lruclock supports atomic operations because there may be multiple threads to obtain the redis clock.

3, Java implementation of LRU algorithm

1. Realization idea

1) Bidirectional linked list -- > insertion time complexity O(1)

We can use a two-way linked list to maintain the order in which data is accessed, and create two virtual nodes: head node and tail node.

The data near the head is the most recently used, while the data near the tail is the longest unused.
When we do put and get operations, we put the data at the head of the linked list.
When the capacity is insufficient to accommodate the new data, remove the data at the end of the linked list first, and then add.

The process of adding data to the linked list header is as follows:

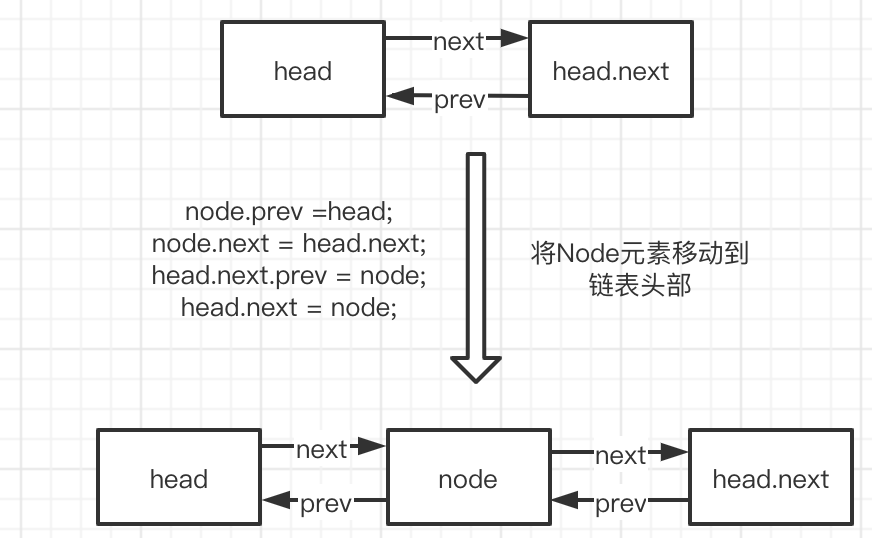
The process of removing data from the linked list is as follows:

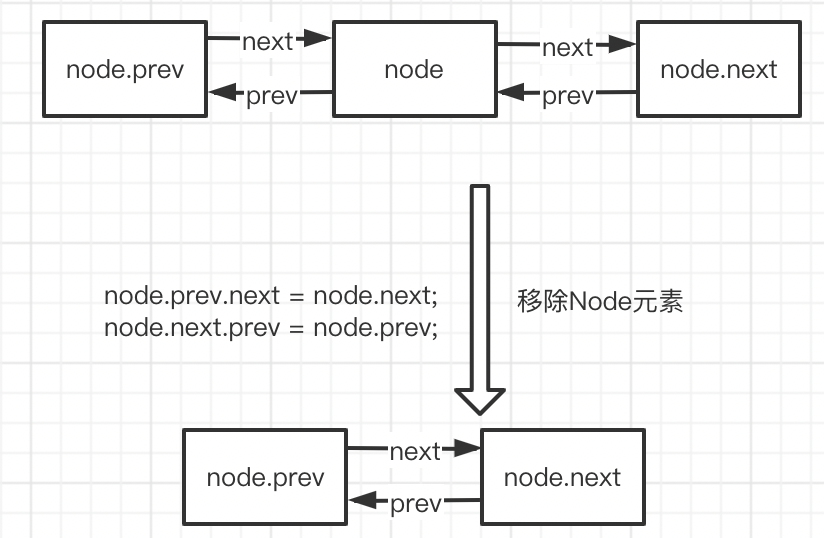
Subsequent implementations are basically based on a combination of these two operations.

However, if only the linked list is used, the average time complexity of the data query is O(n/2). If we make the time complexity of the data query O(1), we need to use the hash table.

The hash table is an ordinary hash map, which maps the key of cached data to the location in the bidirectional linked list.

In this way, we can use the whole LRU data structure, and the time complexity of put and get operations is O(1).
Let's take a look at two ways to realize this idea: one is to rewrite it based on LinkedHashMap, and the other is to make a LinkedHashMap like structure.

Generally speaking, if you are required to handwrite the LRU algorithm in the interview, it is not recommended to write a class directly to inherit from LinkedHashMap for a rewrite operation. The interviewer hopes to investigate your data structure foundation by implementing an LRU data structure yourself.

2. Implementation one (based on LinkedHashMap)

This implementation is simple:

We specify a capacity, use the super keyword to call the constructor of the parent class, and then assign a value to the capacity.
get and put operations also use parent methods.
Override the template method of the parent class – removeEldestEntry(), and customize your own data elimination strategy.

class LRUCache2 extends LinkedHashMap<Integer, Integer> {
    private int capacity;

    public LRUCache2(int capacity) {
        super(capacity, 0.75F, true);
        this.capacity = capacity;
    }

    public int get(int key) {
        return super.getOrDefault(key, -1);
    }

    public void put(int key, int value) {
        super.put(key, value);
    }

    @Override
    protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
        return size() > capacity;
    }
}

3. Implementation 2 (user-defined two-way linked list)

1) Data structure description

The key in the Map corresponds to the LRUNode in the Node one by one, because Java parameters are passed by value, and this value is the memory address of the reference object. Therefore, value in Map < integer, LRUNode >: LRUNode stores the memory address of LRUNode, so you can directly locate the location of LRUNode in the linked list through the key of Map.
Because we need to change the position of data in the linked list with O(1) time complexity, we need to use a two-way linked list, that is, define prev and next nodes in LRUNode.

2) get process

First, judge whether the key exists in the HashMap. If it does not exist, - 1 is returned.
If it exists, it indicates that the node node corresponding to the key is the most recently used node. Locate the node in the linked list through the list, move it to the head of the two-way linked list, and finally return the value value of the node.

3) put process

First, determine whether the key exists
If it does not exist, first create a new Node, then insert the Node into the head of the linked list, and add the key and the key value pair of the Node to the hash table. Finally, judge whether the current size exceeds capacity.
- If it exceeds, the node at the end of the linked list will be removed and its corresponding key call key value pair in the hash table will be deleted.
If it exists, the operation is similar to the get process. First, locate the position of the node in the linked list through the hash table, then update the value of the node to newValue, and finally move it to the head of the two-way linked list.

Note: in the implementation of bidirectional linked list, pseudo header and pseudo tail are used to mark the boundary, so there is no need to check whether its adjacent nodes exist when deleting nodes.

code implementation

/**
 * LRU
 * @author Saint
 */
public class LRUCache {

    private Map<Integer, LRUNode> map;
    private int size;
    private int capacity;

    /**
     * Chain header node and tail node
     */
    private LRUNode head, tail;

    /**
     * Bidirectional linked list node
     */
    class LRUNode {

        private LRUNode prev;

        private LRUNode next;

        private int key;

        private int value;

        public LRUNode() {
        }

        public LRUNode(int key, int value) {
            this.key = key;
            this.value = value;
        }

    }

    public LRUCache(int capacity) {
        map = new HashMap<>(capacity);
        // Virtual head node and tail node
        head = new LRUNode(-1, -1);
        tail = new LRUNode(-1, -1);
        head.next = tail;
        tail.prev = head;
        this.capacity = capacity;
        this.size = 0;
    }

    public int get(int key) {
        LRUNode node = map.get(key);
        if (null == node) {
            return -1;
        }
        // If the key exists, locate it through the hash table, and then move it to the head of the linked list
        moveNodeToHead(node);
        return node.value;
    }

    public void put(int key, int value) {
        LRUNode node = map.get(key);
        // If the key does not exist
        if (null == node) {
            // Create a linked list node
            LRUNode lruNode = new LRUNode(key, value);
            // Add node to linked list header
            addNodeToHead(lruNode);

            // Insert node into hash table
            map.put(key, lruNode);
            ++size;

            if (size > capacity) {
                LRUNode removeTail = removeTail();
                map.remove(removeTail.key);
                --size;
            }
        } else {
            // key already exists
            node.value = value;
            moveNodeToHead(node);
        }
    }

    /**
     * Remove Node from linked list
     */
    public void removeNode(LRUNode node) {
        node.prev.next = node.next;
        // The prev pointer of the next Node of the Node node points to the next of the prev Node of the Node node
        node.next.prev = node.prev;
        // Help GC
        node.next = null;
        node.prev = null;

    }

    /**
     * Move the element to the head of the linked list
     */
    public void addNodeToHead(LRUNode node) {
        node.prev = head;
        node.next = head.next;
        head.next.prev = node;
        head.next = node;
    }

    /**
     * Move the Node to the head of the linked list
     */
    public void moveNodeToHead(LRUNode node) {
        removeNode(node);
        addNodeToHead(node);
    }

    /**
     * Remove the element that has not been accessed for the longest time
     */
    public LRUNode removeTail() {
        LRUNode tailNode = tail.prev;
        removeNode(tailNode);
        return tailNode;
    }

}

PS: the algorithm can be embodied in leetcode 146: https://leetcode-cn.com/problems/lru-cache/

Topics: Java Redis Algorithm

Programmer Think