As a data structure with a very small constant and easy to write, the binary index tree (BIT) is naturally favored by many players. In addition to the well-known sum between intervals and regions, tree array can also replace the huge constant line segment tree to do many things, such as maintaining high-dimensional difference or bisection on BIT, which is the only choice for card constant.

This article mainly introduces the recently encountered tree array maintenance high-dimensional difference and BIT dichotomy. It will be updated when you encounter more usage in the future.

1. BIT dichotomy (multiplication)

Learn CSPs before 2021 and feel that it will be used.

The tree structure of a tree array determines its multiplicative nature. In fact, BIT omits the segment tree of the right son, so the function of the segment tree completely includes BIT, but the cost is a constant of \ (2\sim 10 \) times. By keeping the tree structure of BIT in mind, we can better understand BIT multiplication:

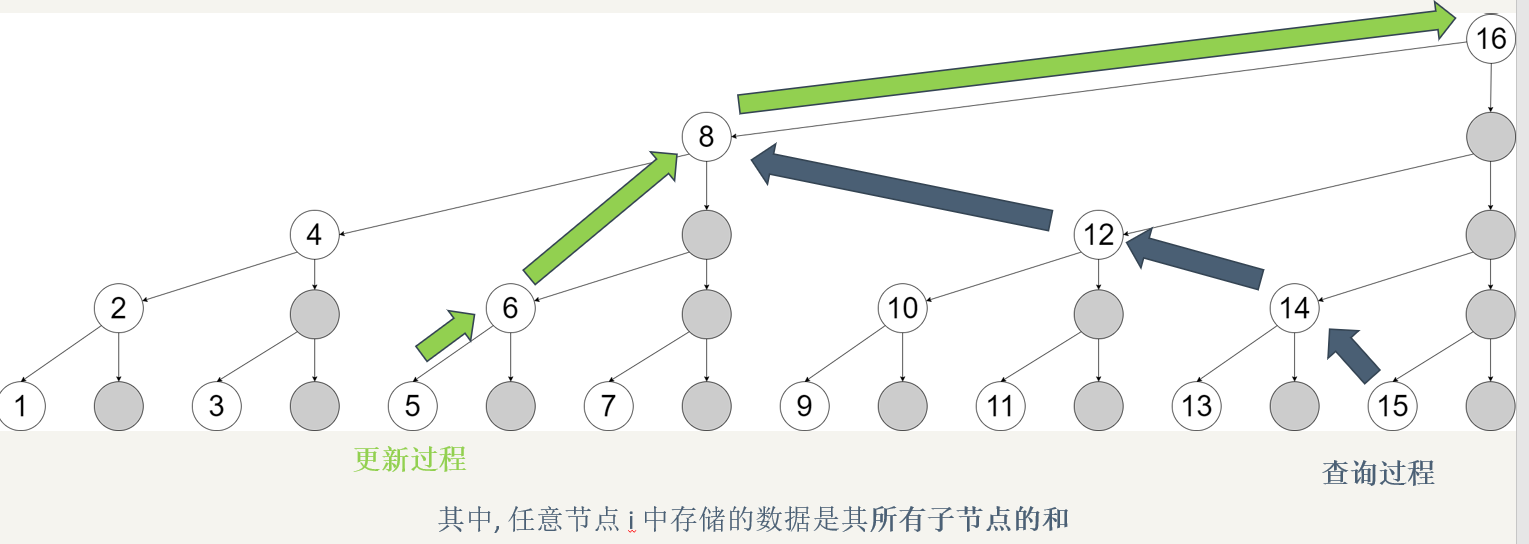
The position with the subscript \ (p \) stores the information and of \ ([l,p] \), where \ (l=p-2^{\mathrm{lowbit}(p)}+1 \) has a length of \ (p-l+1=2^{\mathrm{lowbit}(p)} \), which gives us the condition of multiplication. The specific process is as follows:

Maintain an information prefix and \ (cur \) and the current position \ (p \), and enumerate \ (2^k\leq n \) from large to small. If \ (p+2^k\leq n \) and \ (cur+\mathrm{Information}(p+2^k) \) meet the conditions, make \ (p\gets p+2^k \), otherwise it remains unchanged. The resulting \ (p \) must be the largest and qualified position.

Why is this possible? Note that if we add \ (2^k \) to \ (p \) to meet \ (k < \ mathrm {lowbit} (p) \), then \ (\ mathrm{Information}(p+2^k) \) actually maintains the information and of \ ([p+1,p+2^k] \) (obviously \ (\ mathrm{lowbit}(p+2^k)=k \), so the algorithm is correct.

Of course, the information applicable to such multiplication is still limited to the information that BIT can maintain, but generally speaking \ (\ mathrm{sum} \) is enough to deal with most problems. Let's look at some examples.

I. P6619 [provincial election joint examination 2020 volume a / b] ice Fire Warrior

It's classic.

First, discretize the temperature, so we are looking for the prefix of ice warrior ability about temperature, the suffix of Fire Warrior ability and the maximum value of the smaller value at a certain temperature. Since the abilities are positive integers, the prefix and monotone increase, and the suffix and monotone decrease. Consider maintaining the prefix and sum of the abilities of ice fire warriors with a tree array (the suffix sum is equal to the sum minus the prefix sum), and then find the largest \ (P \) in two, making \ (\ mathrm{Icesum}_p \ Leq \ mathrm {firetotal} - \ mathrm {firesum}{P-1} \) and the largest \ (P \) (it's troublesome to have the largest temperature requirements) Make \ (\ mathrm{Icesum}_p\geq \mathrm{Firetotal}-\mathrm{Firesum}_{p-1} \) and \ (\ mathrm{Icesum}_p \) minimum. Compare the two and take a better solution.

Time complexity \ (\ mathcal{O}(n\log n) \). The optimal solution (10.23) is obtained through the card.

const int N = 2e6 + 5;

int n, lg, cnt, d[N], op[N], t[N], x[N], y[N];
int c1[N], c2[N], Fire;
void add(int x, int v, int *c) {while(x <= cnt) c[x] += v, x += x & -x;}
void query() {
	int p = 0, v1 = 0, v2 = 0;
	for(int i = lg; ~i; i--) {
		int np = p + (1 << i);
		if(np <= cnt && v1 + c1[np] <= Fire - c2[np] - v2)
			p = np, v1 += c1[p], v2 += c2[p];
	}
	if(p < cnt) {
		int x = p + 1, w1 = 0, w2 = 0;
		while(x) w1 += c1[x], w2 += c2[x], x -= x & -x;
		if(v1 <= min(w1, Fire - w2)) {
			v1 = w1, v2 = w2, p = 0;
			for(int i = lg, w2 = 0; ~i; i--) {
				int np = p + (1 << i);
				if(np <= cnt && w2 + c2[np] <= v2) w2 += c2[p = np];
			}
		}
	}
	int ans = min(v1, Fire - v2);
	if(ans) print(d[p]), pc(' '), print(ans << 1), pc('\n');
	else pc('P'), pc('e'), pc('a'), pc('c'), pc('e'), pc('\n');
}

int main(){
	n = read(), lg = log2(n);
	for(int i = 1; i <= n; i++) {
		op[i] = read(), t[i] = read();
		if(op[i] == 1) d[i] = x[i] = read(), y[i] = read();
	} sort(d + 1, d + n + 1), cnt = unique(d + 1, d + n + 1) - d - 1;
	for(int i = 1; i <= n; i++) {
		if(op[i] == 1) {
			x[i] = lower_bound(d + 1, d + cnt + 1, x[i]) - d;
			if(t[i] == 1) Fire += y[i], add(x[i] + 1, y[i], c2);
			else add(x[i], y[i], c1);
		} else {
			int p = t[i];
			if(t[p] == 1) Fire -= y[p], add(x[p] + 1, -y[p], c2);
			else add(x[p], -y[p], c1);
		} query();
	}
    return flush(), 0;
}

2. 2021 noip joint examination Shishi middle school T3 collection

Description of topic meaning: maintain a number heap \ (a_i \), support inserting a number or asking \ (c \), find out the maximum number of times to select \ (c \) and subtract \ (1 \).

\(1\leq a_i\leq 10^9\)，\(1\leq n\leq 10^6\).

An obvious idea is to subtract \ (1 \) from the maximum number of \ (c \) each time (this was only thought of during the game).

There is such a conclusion: find the maximum number \ (v \) and the sum of the remaining numbers \ (s \). If \ (v > \ dfrac s {C-1} \), then \ (v \) must be selected every time. Make \ (c\gets c-1 \) and lose \ (v \). Otherwise \ (v\leq \dfrac{s}{c-1} \), this relationship is still satisfied after each operation, so the answer is \ (\ dfrac{s+v}{c} \).

If we sort all numbers from large to small, we just need to find the last position \ (I \) so that \ (a_i > \ dfrac {\ mathrm {suffixsum} {I + 1} {C-I} \) is slightly deformed to get \ (c > \ dfrac {\ mathrm {suffixsum} {I + 1} {a_i} + I \). It is noted that the two parts of persimmon on the right of the inequality sign increase (not) strictly with the increase of \ (I \) at any time. Therefore, if \ (I \) meets the requirements, any \ (J < I \) meets the requirements and meets the dichotomy. At the same time, adding a number is equivalent to adding a suffix, which can be maintained by BIT, so BIT multiplication is used.

Specifically, we multiply to find the rightmost position \ (P \) so that \ (c > \ dfrac {\ mathrm {suffixsum} {P + 1} {a_p} + P \), then \ (\ dfrac{\mathrm{totalsum} - \mathrm{prefixsum}_p}{c-p} \) is the answer. Time complexity \ (\ mathcal{O}(n\log n) \).

const int N = 1e6 + 5;
int n, u, q, lg, rk[N], qu[N];
ll cnt[N], sum[N];
pii a[N];

int main() {
	cin >> n, lg = log2(n);
	for(int i = 1; i <= n; i++) {
		int op = read();
		if(op == 1) a[++u] = {read(), i};
		else qu[++q] = read();
	}
	sort(a + 1, a + u + 1, [&](pii x, pii y) {return x.fi > y.fi;});
	for(int i = 1; i <= u; i++) rk[a[i].se] = i;
	for(ll i = 1, p = 0, q = 0, tot = 0; i <= n; i++) {
		if(rk[i]) {
			int x = rk[i], v = a[x].fi; q++, tot += v;
			while(x <= u) cnt[x]++, sum[x] += v, x += x & -x;
		} else {
			ll c = qu[++p], x = 0;
			ll csum = 0, ccnt = 0;
			for(int i = lg; ~i; i--) {
				ll nx = x + (1 << i);
				if(nx > n) continue;
				ll v = a[nx].fi;
				ll nsum = csum + sum[nx];
				ll ncnt = ccnt + cnt[nx];
				if(ncnt >= c) continue;
				if(c * v > tot - nsum + ncnt * v)
					x = nx, csum = nsum, ccnt = ncnt;
			}
			print((tot - csum) / (c - ccnt)), pc('\n'); 
		}
	}
	return flush(), 0;
}