Title Description:
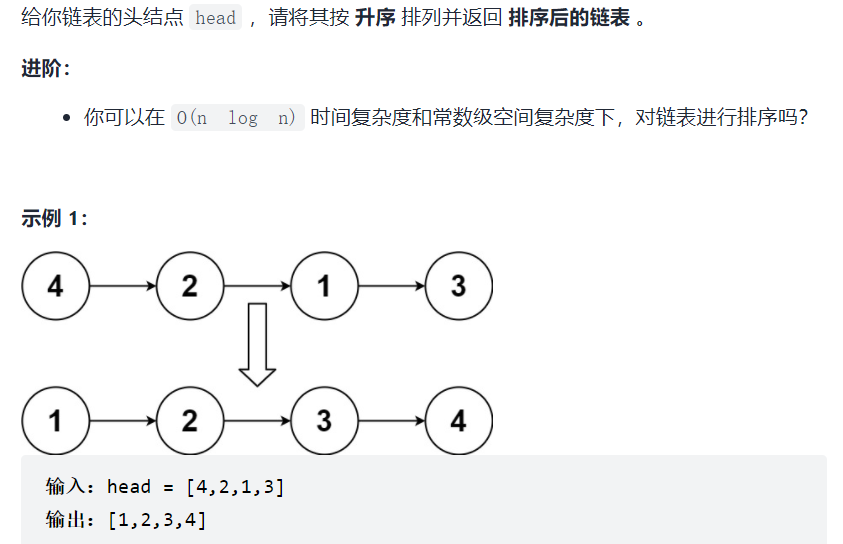
Problem solving ideas:
The advanced problem of the problem requires the time complexity of O(nlogn) and the space complexity of O(1). The sorting algorithm with time complexity of O(nlogn) includes merge sort, heap sort and quick sort (the worst time complexity of quick sort is O(n^2), and the sorting algorithm most suitable for linked list is merge sort.
First recall top-down merging:
Merge sort adopts divide and conquer algorithm to merge the ordered subsequences to obtain a completely ordered sequence.
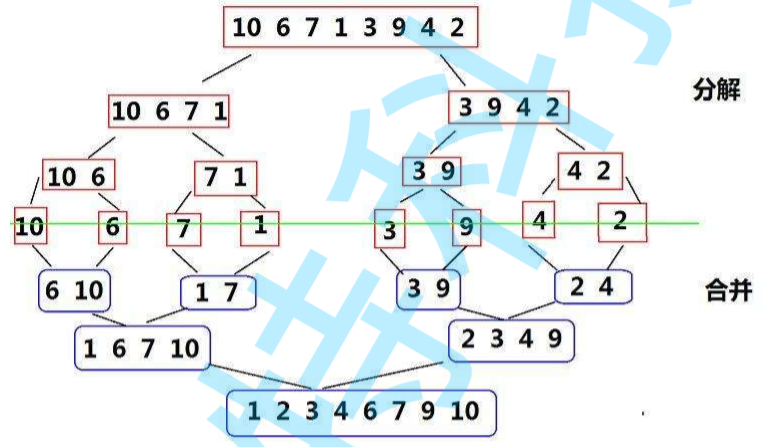
In this problem, first find the middle node of the linked list (you can use the fast and slow pointer), divide the linked list into two parts, and then divide the left and right linked lists respectively until the node is empty or there is only one node left. Here, recursive segmentation can be used. After the segmentation is completed, each sub linked list can be merged.
The code implementation is as follows:
class Solution {
public ListNode sortList(ListNode head) {
return sortList(head,null);
}
public ListNode sortList(ListNode head,ListNode tail) {//Each recursion has a recorded head node and node. The intermediate value passed in by recursion is retained in the next subsequence, so the tail node is set to null. Look back first
//Recursive end condition
if (head == null) return head;
if (head.next == tail) {
head.next = null;//Only the previous node from head to mid is reserved
return head;
}
ListNode slow = head,fast = head;//Speed pointer, find the intermediate node
while (fast != tail) {
fast = fast.next;
slow = slow.next;
if (fast != tail) {
fast = fast.next;
}
}
ListNode mid = slow;
ListNode head1 = sortList(head,mid);//Start recursion, which is paved by the above code. The mid here will be set to null
ListNode head2 = sortList(mid,tail);//The mid here is equivalent to the header node
ListNode new_head = merge(head1,head2);Merge subsequence
return new_head;
}
public ListNode merge(ListNode head1,ListNode head2) {
ListNode dummyHead = new ListNode(-1);//Puppet node
ListNode tmp = dummyHead,tmp1 = head1,tmp2 = head2;
while (tmp1 != null && tmp2 != null) {
if (tmp1.val <= tmp2.val) {
tmp.next = tmp1;
tmp1 = tmp1.next;
} else {
tmp.next = tmp2;
tmp2 = tmp2.next;
}
tmp = tmp.next;
}
if (tmp1 == null) tmp.next = tmp2;
else if (tmp2 == null) tmp.next = tmp1;
return dummyHead.next;
}
}Because top-down merging uses recursive method, the space complexity reaches o (logn), which does not meet the O(1) requirements of the topic, so the bottom-up non recursive sorting method should be adopted here. We can use the iterative method to merge from the smallest cell, and the merged new subsequence continues to merge until the length of the subsequence reaches the original length of the linked list. So in the first step, we require the length of the linked list, and then iterate the time complexity O(N) according to the length. Each time, the length will be reduced by twice, and the time complexity is O (logn). After completing the above steps, the time complexity is O(nlogn), and the space complexity has only defined variables, which is constant complexity O(1).
The code implementation is as follows:
class Solution {
public ListNode sortList(ListNode head) {
if (head == null) return head;
int length = 0;
ListNode node = head;
while (node != null) {//Find the total length
length++;
node = node.next;
}
//Introducing puppet nodes
ListNode dummyHead = new ListNode(0,head);
//Split the linked list into several sub linked lists. The length of the sub linked list starts from 1, followed by 2, 4, 8, 16 Until length is reached.
for (int subLen = 1;subLen < length;subLen <<= 1) {
ListNode prev = dummyHead; //prev is responsible for connecting each ordered sub linked list
ListNode curr = dummyHead.next; //Start position of split linked list
while (curr != null) {//If there is no split end
ListNode head1 = curr; //Record the first sub linked list
for (int i = 1;i < subLen && curr != null && curr.next != null;i++) {
curr = curr.next;
}
ListNode head2 = curr.next; //The length of the first sub linked list reaches subLen, and the next node is the starting position of the second linked list
curr.next = null; //Disconnect the first and second linked lists
curr = head2;
for (int i = 1;i < subLen && curr != null && curr.next != null;i++) {
curr = curr.next; //Start splitting the second linked list with length of subLen
}
ListNode next = null;
if (curr != null) {
next = curr.next; //Record the position of the remaining linked list
curr.next = null; //Disconnect the second linked list from the following list, so that head1 and head2 are two independent linked lists
}
ListNode merge = mergeTwoLists(head1,head2);//Sort and merge into an ordered linked list
prev.next = merge; //Connect the head node of the new sub linked list
while (prev.next != null) {
prev = prev.next; //Go to the end of the ordered linked list and prepare to connect a new sub linked list next time
}
curr = next; //curr starts from the head of the third linked list and is ready to merge with the fourth linked list after sorting
}
}
return dummyHead.next;
}
public ListNode mergeTwoLists(ListNode head1,ListNode head2) {//Merge sub linked list
ListNode dummy = new ListNode(-1);
ListNode cur = dummy;
while (head1 != null && head2 != null) { //Exit the loop as long as one of the linked lists is empty
if (head1.val < head2.val) {
cur.next = head1;
head1 = head1.next;
} else {
cur.next = head2;
head2 = head2.next;
}
cur = cur.next;
}
if (head1 == null) cur.next = head2; //Connect the rest of the unfinished list
else if (head2 == null) cur.next = head1;
return dummy.next;
}
}