Graph theory algorithm
Graph = point + edge undirected graph / directed graph weighted graph / non weighted graph ring (directed graph)
Storage of Graphs
adjacency matrix
#include <iostream>
using namespace std;
int arr[105][105], n, m;
int main() {
cin >> n >> m;
int a, b;
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
arr[a][b] = c;
}
for (int i = 1; i <= n; i++) {
cout << i << " : ";
for (int i = 1; i <= n; j++) {
if (arr[i][j] != 0) {
cout << "{" << i << "-->" << j << "," << arr[i][j] << "} ";
}
}
cout << endl;
}
return 0;
}
How long is dfs a backtracking process
bfs queue traversal
floyd
floyd algorithm -- multi-source shortest path slow O(N^3) simple
for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) for (int k = 1; k <= n; k++) arr[j][k] = min(arr[j][k], arr[j][i] + arr[i][k])
There is a negative ring (the path of a ring is negative) and there is no shortest path
#include <iostream>
#include <cstring>
using namespace std;
int arr[1005][1005], n, m, s;
int main() {
memset(arr, 0x3f, sizeof(arr));
cin >> n >> m >> s;
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
if (arr[a][b] > c) {
arr[a][b] = c;
arr[b][a] = c;
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= n; k++) {
arr[j][k] = min(arr[j][k], arr[j][i] + arr[i][k]); }
}
}
for (int i = 1; i <= n; i++) {
arr[i][i] = 0;
if (arr[s][i] == 0x3F3F3F3F) {
cout << -1 << endl;
} else {
cout << arr[s][i] << endl;
}
}
return 0;
}
Adjacency table
Only useful edges are stored, saving space to check edges O(N)
Adjacency table 1
#include <iostream>
using namespace std;
int n, m, edg[105][105];
int main() {
cin >> n >> m;
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
edge[a][++edge[a][0]] = b; // edge[a][0] - number of edges of point a
}
for (int i = 1; i <= n; i++) {
cout << i << " : ";
for (int j = 1; j <= edge[i][0]; j++) {
cout << edge[i][j] << " ";
}
cout << endl;
}
return 0;
}
Adjacency table 2
#include <iostream>
#include <vector>
using namespace std;
struct node {
int s, e, v;
};
int main() {
int n, m;
cin >> n >> m;
vector<vector<edge> > edg(n + 5, vector<edge>());
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
edge[a].push_back((edge{a, b, c}));
//edge[b].push_back((edge{b, a, c}));
}
for (int i = 1; i <= n; i++) {
cout << i << " : ";
for (int j = 0; j < edg[i].size(); j++) {
cout << "{" << i/*edg[i][j].s*/ << "--> "edge[i][j].e << "," << edg[i][j].v << "}";
}
cout << endl;
}
return 0;
}
dijkstra
1. Select a point n closest to point v from S
2. Update the distance of all points in S from point v
shortest path Time complexity O((E + V) * log(V))
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
struct node {// now point, dis distance
int now, dis;
bool operator< (const node &b) const {
return this->dis > b.dis;
}
};
struct edge {// e end point, v weight
int e, v;
};
int main() {
int n, m, s, ans[100005];
memset(ans, 0x3f, sizeof(ans));
cin >> n >> m >> s;
vector<vector<edge> > edg(n + 5, vector<edge>());
for (int i = 0; i < m; i++) { // Edge insertion, heavy edge untreated
int a, b, c;
cin >> a >> b >> c;
edg[a].push_back((edge{b, c}));
edg[b].push_back((edge{a, c}));
}
priority_queue<node> que;
que.push((node){s, 0});//Start in queue
ans[s] = 0; //Starting point weight removal
while (!que.empty()) { //dijkstra
node temp = que.top();
que.pop();//Take out the shortest circuit from the status
if (ans[temp.now] < temp.dis) {// The edge of ans is already the optimal solution and does not need to be updated
continue;
}
for (int i = 0; i < edg[temp.now].size(); i++) {
int e = edg[temp.now][i].e, v = edg[temp.now][i].v;
if (ans[e] > temp.dis + v) {//Traverse to temp Each edge with now as the starting point
ans[e] = temp.dis + v; //Update distance
que.push((node){e, ans[e]});//Drop it into the priority queue to prepare for subsequent node updates
}
}
}
for (int i = 1; i <= n; i++) {
if (ans[i] == 0x3f3f3f3f) {
cout << -1 << endl;
}
else {
cout << ans[i] << endl;
}
}
return 0;
}
Chain forward star
Similar adjacency multiple tables (better)
E V next (number of the next side of the same starting point)
Array analog linked list (header insertion method)
Code demonstration
#include <iostream>
#include <cstring>
using namespace std;
struct edge {
int e, v, next;
};
edge edg[1005];
int n, m, head[1005]; //The head array records the head node
int main() {
memset(head, -1, sizeof(head));
cin >> n >> m;
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
edg[i].e = b; //End
edg[i].v = c; //Weight
edg[i].next = head[a]; //Similar to head interpolation, head[a] records the previous edge
head[a] = i; //Update header node
}
for (int i = 1; i <= n; i++) {
cout << i << " : ";
for (int j = head[i]; j != -1; j = edg[j].next) {
cout << "{" << i << "-->" << edg[j].e << "," << edg[j].v << "}";
}
cout << endl;
}
return 0;
}
dijkstra + Chain forward star
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
struct edge {
int e, v, next;
};
struct node {// now point, dis distance
int now, dis;
bool operator< (const node &b) const {
return this->dis > b.dis;
}
};
edge edg[200005];
int n, m, s, ans[100005], head[100005], cnt;
void add_edge(int a, int b, int c) {//Chain forward star
edg[cnt].e = b;
edg[cnt].v = c;
edg[cnt].next = head[a];
head[a] = cnt;
cnt++;
}
int main() {
memset(head, -1, sizeof(head));
memset(ans, 0x3F, sizeof(ans));
cin >> n >> m >> s;
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
add_edge(a, b, c);
add_edge(b, a, c);
}
priority_queue<node> que;
que.push((node){s, 0});
ans[s] = 0;
while (!que.empty()) {
node temp = que.top();
que.pop();
if (temp.dis > ans[temp.now]) {
continue;
}
for (int i = head[temp.now]; i != -1; i = edg[i].next) {
int e = edg[i].e, v = edg[i].v;
if (ans[e] > ans[temp.now] + v) {
ans[e] = ans[temp.now] + v;
que.push((node){e, ans[e]});
}
}
}
for (int i = 1; i <= n; i++) {
if (ans[i] == 0x3f3f3f3f) {
cout << -1 << endl;
} else {
cout << ans[i] << endl;
}
}
return 0;
}
Bellman-ford
The shortest single source path from the edge to the point
Initialized to a maximum value, each round of update traverses all edges
Through edge
Use the short circuit of the edge start point + the weight of the edge to update the answer of the edge end point
The data complexity is O(N*M). The shortest path of updating a point in each round allows negative edges
Execute n-wheel, update the shortest circuit to the origin once every time you traverse all the edges
#include <iostream>
#include <cstring>
using namespace std;
struct edge {
int s, e, v;
};
edge edg[200005];
int n, m, s, ans[100005];
void add_edge(int a, int b, int c) {
edg[cnt].s = a;
edg[cnt].e = b;
edg[cnt].v = c;
cnt++;
}
int main() {
memset(ans, 0x3f, sizeof(ans));
cin >> n >> m >> s;
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
add_edge(a, b, c);
add_edge(b, a, c);
}
for (int i = 0; i <= n; i++) {//How many rounds
int f = 0;
for (int j = 0; j < cnt; j++) {// Traverse all edges in each round
if (ans[edg[j].e] > ans[edg[j].s] + edg[j].v) {
ans[edg[j].e] = ans[edg[j].s] + edg[j].v;
f = 1;
}
}
if (f == 0) break; //This round does not update any points, that is, the update is complete
}
for (int i = 1; i <= n; i++) {
if (ans[i] == 0x3f3f3f3f) {
cout << -1 << endl;
} else {
cout << ans[i] << endl;
}
}
return 0;
}
Only the points updated in the previous round can affect the next round of updates
Queue based Bellman_ Optimization of Ford
The worst time complexity is still O(N*M), the time complexity is unstable, and the speed is metaphysical
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
struct edge {
int e, v, next;
};
edge edg[200005];
int n, m, s, ans[100005], head[100005], cnt, mark[100005];//mark every round of weight removal
void add_edge(int a, int b, int c) { //Chain forward star
edg[cnt].e = b;
edg[cnt].v = c;
edg[cnt].next = head[a];
head[a] = cnt++;
}
int main() {
memset(ans, 0x3f, sizeof(ans));
memset(head, -1, sizeof(head));
cin >> n >> m >> s;
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
add_edge(a, b, c);
add_edge(b, a, c);
}
queue<int> que;
ans[s] = 0;
que.push(s); //Start and join the team
mark[s] = 1;
while (!que.empty()){
int temp = que.front();//Previously updated points
que.pop();
mark[temp] = 0;
for (int i = head[temp]; i != -1; i = edg[i].next) {//All the edges starting from this point are used to update the end point of the edge
int e = edg[i].e, v = edg[i].v;
if (ans[e] > ans[temp] + v) {
ans[e] = ans[temp] + v;
if (mark[e] == 0) {
que.push(e);
mark[e] = 1;
}
}
}
}
for (int i = 1; i <= n; i++) {
if (ans[i] == 0x3f3f3f3f) {
cout << -1 << endl;
} else {
cout << ans[i] << endl;
}
}
return 0;
}
summary
Adjacency matrix n*n, y relation
Table m
Linked forward star uses pointer field to simulate linked list
shortest path
floyd multi-source, slow
dijkstra single source, stable and fast, can not have negative weight edge
bellman_ford single source, slow
Bellman with queue optimization_ Ford, speed metaphysics, instability
Hospital settings
#include <iostream>
#include <cstring>
using namespace std;
int n, num[105], arr[105][105];
int main() {
memset(arr, 0x3F, sizeof(arr));
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> num[i];
int a, b;
cin >> a >> b;
if (a) {
arr[i][a] = 1;
arr[a][i] = 1;
}
if (b) {
arr[i][b] = 1;
arr[b][i] = 1;
}
arr[i][i] = 0;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= n; k++) {
arr[j][k] = min(arr[j][k], arr[j][i] + arr[i][k]);
}
}
}
int ans = 0X3f3f3f3f;
for (int i = 1; i <= n; i++) {
int t = 0;
for (int j = 1; j <= n; j++) {
t += arr[j][i] * num[j];
}
ans = min(ans, t);
}
cout << ans << endl;
return 0;
}
Post disaster reconstruction floyd modification
Just change the floyd outermost loop
#include <iostream>
#include <cstring>
using namespace std;
int n, m, q, num[205], now, arr[205][205]; //Now, now, we have to fix the number one, num
int main(){
memset(arr, 0x3f, sizeof(arr));
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> num[i];
arr[i][i] = 0;
}
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
a++, b++;
arr[a][b] = arr[b][a] = c;
}
cin >> q;
for (int i = 0; i < q; i++) {
int x, y, t;
cin >> x >> y >> t;
x++, y++;
while (num[now] <= t && now <= n) {
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= n; k++) {
arr[j][k] = min(arr[j][k], arr[j][now] + arr[now][k]);
}
}
now++;
}
if (num[x] > t || num[y] > t || arr[x][y] == 0x3f3f3f3f) {
cout << -1 << endl;
} else {
cout << arr[x][y] << endl;
}
}
return 0;
}
Common questions and skills P1
Prefix and
Fast solving interval sum
Find the sum of bit 0 to the current bit
Ask O(1)
Space complexity O(N)
303. Region and retrieval - array immutable
class NumArray {
public:
int sum[10005] = {0};
NumArray(vector<int>& nums) {
for (int i = 0; i < num.size(); i++) {//The overall backward offset is one bit, excluding the endpoint i + 1
sum[i + 1] = sum[i] + nums[i];
}
}
int sumRange(int left, int right) {
return sum[right + 1] - sum[left];
}
};
304. Two dimensional area and retrieval - the matrix is immutable
Prefix and 3-block calculation of two-dimensional array
class NumMatrix {
public:
int n, m;
vector<vector<int> > sum;
NumMatrix(vector<vector<int>>& matrix) {
n = matrix.size(), m = matrix[0].size();
sum = vector<vector<int> >(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
sum[i][j] = matrix[i][j];
if (i - 1 >= 0) {
sum[i][j] += sum[i - 1][j];
}
if (j - 1 >= 0) {
sum[i][j] += sum[i][j - 1];
}
if (i - 1 >= 0 && j - 1 >= 0){
sum[i][j] -= sum[i - 1][j - 1];
}
}
}
}
int sumRegion(int r1, int c1, int r2, int c2) {
int ans = sum[r2][c2];
if (r1 - 1 >= 0) {
ans -= sum[r1 - 1][c2];
}
if (c1 - 1 >= 0) {
ans -= sum[r2][c1 - 1];
}
if (c1 - 1 >= 0 && r1 -1 >= 0) {
ans += sum[r1 - 1][c1 - 1];
}
return ans;
}
};
Search map
1. Connectivity
2. Minimum steps
Queue (node) + direction array + judgment and de duplication
#include <iostream>
#include <queue<
using namespace std;
struct node {
int x, y, step;
};
int n, m, sx, sy, ex, ey;
int dir[8][2] = {0, 1, 1, 0, 0, -1, -1, 0, 1, 1, 1, -1, -1};
char mmap[105][105];
void p(int cnt) {
cout << "--------------------" << cnt << "--------------------" << endl;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cout << mmap[i][j]; //Print new points first, and then change to old points
if (mmap[i][j] == 'x') {
mmap[i][j] = 'X'; //Earlier point
}
}
cout << endl;
}
cout << "------------------------------------------" << endl;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= m; j++) {
cin >> mmap[i][j];
if (mmap[i][j] == 'S') {
sx = i, sy = j;
}
if (mmap[i][j] == 'T') {
ex = i, ey = j;
}
}
queue<node> que;
que.push((node){sx, sy, 0});
int cnt = 0;
while (!que.empty()) {
node temp = que.front;
que.pop();
for (int i = 0; i < 8; i++) {
int x = temp.x + dir[i][0];
int y = temp.y + dir[i][1];
if (mmap[x][y] == 'T') {
cout << temp.step + 1 << endl;
return 0;
}
if (mmap[x][y] == '.') {
que.push((node){x, y, temp.step + 1});
mmap[x][y] = 'x'; //duplicate removal
cnt++; //How many points did you go
if (cnt % 10 == 0) {
p(cnt);
}
}
}
}
return 0;
}
heuristic search
The essence is to estimate the distance to the destination, use the priority queue to replace the wide search queue, demonstrate the relevant visual code, and finally output a specified optimal solution
How far is the starting point + how far is the ending point? European distance of priority queue, one of which is A*
#include <iostream>
#include <queue>
#include <cmath>
using namespace std;
struct node {
int x, y, step;
double h;
bool operator< (const node &b) const {
return step + h > b.step + b.h; // Small priority Small top reactor - less than to greater than Large top pile - less than any
}
};
int n, m, sx, sy, ex, ey, fx[105][105], fy[105][105];
int dir[8][2] = {0, 1, 1, 0, 0, -1, -1, 0, 1, 1, 1, -1, -1}; //Eight directions
char mmap[105][105];
double dis(int x, int y) {
int t1 = x - ex, t2 = y - ey;
return sqrt(t1 * t1, t2 * t2);
}
void p(int cnt) {
cout << "--------------------" << cnt << "--------------------" << endl;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cout << mmap[i][j];
if (mmap[i][j] == 'x') {
mmap[i][j] = '~';
}
}
cout << endl;
}
cout << "------------------------------------------" << endl;
}
void func(int x, int y) {
if (mmap[x][y] == 'S') return;
mmap[x][y] = 'o';
func(fx[x][y], fy[x][y]); //Dad's x and y
}
int main() {
cin >> n >> m;
for (int i = 1; i <= m; j++) {
cin >> mmap[i][j];
if (mmap[i][j] == 'S') {
sx = i, sy = j;
}
if (mmap[i][j] == 'T') {
ex = i, ey = j;
}
}
priority_queue<node> que;
que.push((node){sx, sy, 0, dis(sx, sy)});
int cnt = 0;
while (!que.empty()) {
node temp = que.top();
que.pop();
for (int i = 0; i < 8; i++) {
int x = temp.x + dir[i][0];
int y = temp.y + dir[i][1];
if (mmap[x][y] == 'T') {
func(temp.x, temp.y);
p(cnt);
cout << temp.step + 1 << endl;
return 0;
}
if (mmap[x][y] == '.') {
fx[x][y] = temp.x; //Dad's x
ft[x][y] = temp.y; //Dad's y
mmap[x][y] == 'x';
que.push((node){x, y, temp.step + 1, dis(x, y)});//The shortest calculation of dis is preferred
cnt++;
if (cnt % 5 == 0) {
p(cnt);
}
}
}
}
cout << -1 << endl;
return 0;
}
LRU caching mechanism
Implement LRUCache class:
- LRUCache(int capacity) initializes the LRU cache with a positive integer as capacity
- int get(int key) if the keyword key exists in the cache, the value of the keyword is returned; otherwise, - 1 is returned.
- void put(int key, int value) if the keyword already exists, change its data value; If the keyword does not exist, insert the group keyword value. When the cache capacity reaches the maximum, it should delete the longest unused data value before writing new data, so as to make room for new data values.
class LRUCache {
public:
struct node {
int key, val;
node *front, *back;
node() {
key = -1, val = -1;
front = back = nullptr;
}
node (int k, int v) {
key = k, val = v;
front = back = nullptr;
}
};
node *l, *r;//Virtual head virtual tail
int mmax, now;
unordered_map<int, node*> m;
LRUCache(int capacity) {
mmax = capacity, now = 0;
l = new node();
r = new node();
l->back = r;
r->front = l;
}
void push_frt(node *p) { // Head insert
if (p->front != nullptr) { //Adjust the elements around p and delete p
p->front->back = p->back;
p->back->front = p->front;
}
p->back = l->back;
p->front = l;
l->back->front = p;
l->back = p;
}
void del_back() {
node *p = r->front;
m.erase(p->key);
p->front->back = r;
r->front = p->front;
delete p;
}
int get(int key) {
if (m.count(key)) {
push_frt(m[key]);
return m[key]->val;
}
return -1;
}
void put(int key, int value) {
node *p;
if (m.count(key) == 0) {
p = new node(key, value);
m[key] = p;
now++;
} else {
p = m[key];
p->val = value;
}
push_frt(p);
if (now > mmax) {
now--;
del_back();
}
}
};
The postman delivers the letter
Start end interchange
Bellman Ford + Chain forward star
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
struct edge {
int e, v, next;
};
edge edg[2][100005];
int n, m, ans[2][100005], head[2][100005], mark[100005];
void add_edg(int cnt, int ind, int s, int e, int v) {
edg[cnt][ind].e = e;
edg[cnt][ind].v = v;
edg[cnt][ind].next = head[cnt][s];
head[cnt][s] = ind;
}
void func(int cnt) {
memset(mark, 0, sizeof(mark));
queue<int> que;
que.push(1);
ans[cnt][1] = 0;
mark[1] = 1;
while (!que.empty()) {
int temp = que.front();
que.pop();
mark[temp] = 0;
for (int i = head[cnt][temp]; i != -1; i = edg[cnt][i].next) {
int e = edg[cnt][i].e, v = edg[cnt][i].v;
if (ans[cnt][e] > ans[cnt][temp] + v) {
ans[cnt][e] = ans[cnt][temp] + v;
if (mark[e] == 0) {
mark[e] = 1;
que.push(e);
}
}
}
}
}
int main() {
memset(head, -1, sizeof(head));
memset(ans, 0x3f, sizeof(ans));
cin >> n >> m;
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
add_edg(0, i, a, b, c);
add_edg(1, i, b, a, c); //Transformer single source shortest circuit
}
func(0);
func(1);
long long sum = 0;
for (int i = 2; i <= n; i++) {
sum += ans[0][i] + ans[1][i];
}
cout << sum << endl;
return 0;
}
Common problems and skills P2
Delete the penultimate node of the linked list
1. Virtual head node (convenient for head node operation)
2. The left and right pointers move back N times, and then move left and right together. When the right pointer points to null, the next element of the left pointer can be deleted
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode *root = new ListNode(0, head); //Create virtual head node
ListNode *l = root, *r = head;
for (int i = 0; i < n; i++) {
r = r->next;
}
while (r != nullptr) {
l = l->next;
r = r->next;
}
ListNode *p = l->next;
l->next = l->next->next;
delete p;
ListNode *pp = root->next;
delete root;
return pp;
}
};
Exchange the nodes in the linked list
1. Virtual head node
2. P pointer, exchange p - > next and P - > next - > next;
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode *root = new ListNode(0, head);
ListNode *t = root;
while (t->next != nullptr && t->next->next != nullptr) {
ListNode *l = t->next;
ListNode *r = t->next->next;
l->next = r->next;
r->next = l;
t->next = r;
t = l;
}
ListNode *p = root->next;
delete root;
return p;
}
};
Delete duplicate elements in the sorting linked list
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* deleteDuplicates(ListNode* head) {
if (head == nullptr) return head;
ListNode *p = head;
while (p->next != nullptr) {
if (p->next->val == p->val) {
ListNode* t = p->next;
p->next = p->next->next;
delete t;
} else {
p = p->next;
}
}
return head;
}
};
Delete duplicate Element II in the sorting linked list
Left and right pointer
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* deleteDuplicates(ListNode* head) {
if (head == nullptr || head->next == nullptr) return head;
ListNode *root = new ListNode(0, head);
ListNode *l = root;
while (l->next != nullptr) {
ListNode *r = l->next->next;
while (r != nullptr && r->val == l->next->val) {
r = r->next;
}
if (r == l->next->next) { //No element deleted
l = l->next;
} else { //Deleted element
l->next = r;
}
}
return root->next;
}
};
Circular linked list
Fast and slow pointer
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
bool hasCycle(ListNode *head) {
if (head == nullptr) return false;
ListNode *slow = head, *fast = head;
while (fast != nullptr && fast->next != nu;;ptr) {
fast = fast->next->next;
slow = slow->next;
if (fast == slow) {
return true;
}
}
return false;
}
};
Circular linked list II
The fast and slow pointer block pointer has twice the path as the slow pointer
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *slow = head, *fast = head;
while(true){
if(fast == nullptr || fast->next == nullptr){
return nullptr;
}
slow = slow->next;
fast = fast->next->next;
if(slow == fast){
break;
}
}
fast = head;
while(slow != fast){
fast = fast->next;
slow = slow->next;
}
return slow;
}
};
Intersection list
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if (headA == nullptr || headB == nullptr) {
return nullptr;
}
ListNode *a = headA, *b = headB;;
int f = 0;
while (1) {
if (a == b) {
return a;
}
if (a->next == nullptr) {
a = headB;
f++;
} else {
a = a->next;
}
if (b->next == nullptr) {
b = headA;
f++;
} else {
b = b->next;
}
if (f > 2) {
break;
}
}
return nullptr;
}
};
Happy number
Fast or slow pointer or hash
class Solution {
public:
int num[10] = {0, 1, 4, 9, 16, 25, 36, 49, 64, 81};
int func(int x) {
int t = 0;
while (x) {
t += num[x % 10];
x /= 10;
}
return t;
}
bool isHappy(int n) {
int slow = n, fast = n;
while (fast != 1) {
fast = func(fast);
fast = func(fast); //Quick pointer
slow = func(slow);
if (fast == 1) {
break;
}
if (fast == slow) {
return false;
}
}
return true;
}
};
Remove linked list elements
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
if (head == nullptr) return head;
ListNode *root = new ListNode(0, head);
ListNode *l = root;
while(l != nullptr && l->next != nullptr) {
ListNode *r = l->next;
while(r != nullptr && r->val == val) {
r = r->next;
}
l->next = r;
l = l->next;
}
return root->next;
}
};
Reverse linked list
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if (head == nullptr || head->next == nullptr) return head;
ListNode *l = head, *r = head->next;
l->next = nullptr;
while (r != nullptr) {
ListNode *t = r->next;
r->next = l;
l = r;
r = t;
}
return l;
}
};
Delete node in linked list
use a corpse to resurrect a dead soul
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
void deleteNode(ListNode* node) {
node->val = node->next->val;
node->next = node->next->next;
}
};
Verify stack sequence
class Solution {
public:
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
stack<int> sta;
int n = pushed.size();
for (int i = 0, j = 0; i < n; i++) { //Simulated out of stack
while (sta.empty() || sta.top() != popped[i]) { //If the stack top does not match, it will be stacked
if (j == n) {
return false;
}
sta.push(pushed[j]);//Push
j++;
}
sta.pop();//Stack when matching
}
return true;
}
};
Compare strings with backspace
Two stacks
class Solution {
public:
bool backspaceCompare(string s, string t) {
stack<char> s1, s2;
for (auto c : s) {
if (c == '#') {
if (!s1.empty()) {
s1.pop();
}
} else {
s1.push(c);
}
}
for (auto c : t) {
if (c == '#') {
if (!s2.empty()) {
s2.pop();
}
} else {
s2.push(c);
}
}
while (!s1.empty() && !s2.empty()) {
if (s1.top() != s2.top()) {
return false;
}
s1.pop();
s2.pop();
}
if (s1.empty() && s2.empty()) {
return true;
}
return false;
}
};
Deletes all adjacent duplicates in the string
Stack simulation
class Solution {
public:
string removeDuplicates(string s) {
stack<char> sta;
for (auto c : s) {
if (sta.empty() || sta.top() != c) {
sta.push(c);
} else {
sta.pop();
}
}
string ans;
while (!sta.empty()) {
ans += sta.top;
sta.pop();
}
reverse(ans.begin());
return ans;
}
};
Graph theory algorithm
minimum spanning tree
kruskal = edge sorting + joint search set
#include <iostream>
#include <algorithm>
using namespace std;
struct edge {
int s, e, v;
bool operator< (const edge& b) const {
return this->v < b.v;
}
};
edge edg[200005];
int n, m, ans, my_union[5005], cnt;
void init() {
for (int i = 1; i <= n; i++) {
my_union[i] = i;
}
}
int find_fa(int x) {
if (my_union[x] == x) {
return x;
}
return my_union[x] = find_fa(my_union[x]);
}
int main() {
cin >> n >> m;
for (int i = 0; i < m; i++) {
cin >> edg[i].s >> edg[i].e >> edg[i].v;
}
sort(edg, edg + m);
init();
for (int i = 0; i < m; i++) {
int s = edg[i].s, e = edg[i].e, v = edg[i].v;
int fa = find_fa(s), fb = find_fa(e);
if (fa != fb) {
my_union[fa] = fb; // Merge two sets
ans += v;
cnt++;
if (cnt == n - 1) { // n - 1 edges selected
cout << ans << endl; // Output the total length of the minimum spanning tree
return 0;
}
}
}
cout << "orz" << endl; // Minimum spanning tree does not exist
return 0;
}
prim extends from one point (select the shortest path)
1. Priority queue (select the minimum point (to the current point set))
2. Traverse all edges of a starting point (adjacency list / chained forward star is more convenient)
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
struct node {
int e, v;
bool operator< (const node &b) const {
return this->v > b.v;
}
};
struct edge {
int e, v, next;
};
edge edg[4000005];
int n, m, head[5005], mark[5005], ans, cnt, edg_cnt, num[5005];//num[x] represents the weight connected to the X edge mark indicates whether a point is connected
void add_edg(int a, int b, int c) {
edg[edg_cnt].e = b;
edg[edg_cnt].v = c;
edg[edg_cnt].next = head[a];
head[a] = edg_cnt++;
}
int main() {
memset(head, -1, sizeof(head)); //-1 end point
memset(num, 0x3f, sizeof(num));
cin >> n >> m;
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
add_edg(a, b, c);
add_edg(b, a, c);
}
priority_queue<node> que;
que.push((node){n / 2, 0}); // Any point as the starting point
while (!que.empty()) {
node temp = que.top();
que.pop();
if (mark[temp.e] == 1) { //Already connected
continue;
}
ans += temp.v;
mark[temp.e] = 1;
cnt++;
if (cnt == n) { //Connected n points
cout << ans << endl;
return 0;
}
for (int i = head[temp.e]; i != -1; i = edg[i].next) {//Traverse to temp E is the starting edge
int e = edg[i].e, v = edg[i].v;
if (mark[e] == 0 && num[e] > v) {// If the current edge is less than num[e], it will join the priority queue, which can be omitted
que.push((node){e, v});
num[e] = v;
}
}
}
cout << "orz" << endl;
return 0;
}
Highway construction
prim point edge current use current demand
#include <iostream>
#include <cstring>
#include <queue>
#include <math.h>
#include <stdio.h>
using namespace std;
struct node {
int e;
double v;
bool operator< (const node &b) const {
return this->v > b.v;
}
};
int n, xy[50005][2], mark[5005], cnt;
double num[5005], ans;
double func(int a, int b) {
long long t1 = xy[a][0] - xy[b][0];
long long t2 = xy[a][1] - xy[b][1];
return sqrt(t1 * t1 + t2 * t2);
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> xy[i][0] >> xy[i][1];
num[i] = 99999999999;
}
priority_queue<node> que;
que.push((node){1, 0});
while (!que.empty()) {
node temp = que.top();
que.pop();
if (mark[temp.e] == 1) continue;
ans += temp.v;
cnt++;
mark[temp.e] = 1;
if (cnt == n) {
printf("%.2f\n", ans);
return 0;
}
for (int i = 1; i <= n; i++) {
if (mark[i] == 0 && i != temp.e) {
double t = func(temp.e, i);
if (num[i] > t) {
num[i] = t;
que.push((node) {i, t});
}
}
}
}
}
Wireless communication network
Find the n - k long side of the minimum spanning tree after deleting k points
#include <iostream>
#include <algorithm>
#include <cmath>
#include <stdio.h>
using namespace std;
struct edge {
int s, e;
double v;
};
bool cmp(const edge &a, const edge &b) {
return a.v < b.v;
}
edge edg[250005];
int k, n, my_union[505], xy[505][2], edg_cnt, cnt;
void init() {
for (int i = 1; i <= n; i++) {
my_union[i] = i;
}
}
int find_fa(int x) {
if (my_union[x] == x) {
return x;
}
return my_union[x] = find_fa(my_union[x]);
}
int main() {
cin >> k >> n;
init();
for (int i = 1; i <= n; i++) {
cin >> xy[i][0] >> xy[i][1];
for (int j = 1; j < i; j++) { // Dynamically find the length of all edges
int t1 = xy[i][0] - xy[j][0];
int t2 = xy[i][1] - xy[j][1];
edg[edg_cnt].s = i;
edg[edg_cnt].e = j;
edg[edg_cnt++].v = sqrt(t1 * t1 + t2 * t2);
}
}
sort(edg, edg + edg_cnt, cmp);
for (int i = 0; i < edg_cnt; i++) {
int s = edg[i].s, e = edg[i].e;
double v = edg[i].v;
int fa = find_fa(s), fb = find_fa(e);
if (fa != fb) {
my_union[fa] = fb;
cnt++;
if (cnt == n - k) {
printf("%.2f\n", v);
return 0;
}
}
}
return 0;
}
Shortest circuit count
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
struct node {// now point, dis distance
int now, dis;
bool operator< (const node& b) const {
return this->dis > b.dis;
}
};
struct edge {// e end point, v weight
int e, v;
};
int ans1[100005]; //Number of schemes
int main() {
int n, m, s, ans[100005];
memset(ans, 0x3f, sizeof(ans));
cin >> n >> m;
for (int i = 1; i <= n; i++) { // init
ans1[i] = 1;
}
s = 1;
vector<vector<edge> > edg(n + 5, vector<edge>());
for (int i = 0; i < m; i++) { // Edge insertion, heavy edge untreated
int a, b, c;
cin >> a >> b;
c = 1;
edg[a].push_back((edge{ b, c }));
edg[b].push_back((edge{ a, c }));
}
priority_queue<node> que;
node t = { s, 0 };
que.push(t);//Start in queue
ans[s] = 0; //Starting point weight removal
while (!que.empty()) { //dijkstra
node temp = que.top();
que.pop();//Take out the shortest circuit from the status
if (ans[temp.now] < temp.dis) {// It is already a better solution and does not need to be updated
continue;
}
for (int i = 0; i < edg[temp.now].size(); i++) {
int e = edg[temp.now][i].e, v = edg[temp.now][i].v;
if (ans[e] > temp.dis + v) {//Traverse to temp Each edge with now as the starting point
ans[e] = temp.dis + v; //Update distance
ans1[e] = ans1[temp.now];
t = { e, ans[e] };
que.push(t);//Drop it into the priority queue to prepare for subsequent node updates
}
else if (ans[e] == temp.dis + v) {
ans1[e]= (ans1[e] + ans1[temp.now]) % 100003;
}
}
}
for (int i = 1; i <= n; i++) {
if (ans[i] == 0x3f3f3f3f) {
cout << 0 << endl;
}
else {
cout << ans1[i] << endl;
}
}
return 0;
}
Topological sorting
1. Directed graph 2. Not unique 3. There can be no rings in the graph
Find the penetration of each node
Take out a point with a penetration of 0, get a new graph, and calculate the penetration of each node
repeat
Keep taking out points with penetration of 0
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
struct edge {
int e, next;
};
edge edg[100005];
int n, m, head[105], in_degreee[105], ans[105], cnt;
int main() {
memset(head, -1, sizeof(head));
cin >> n >> m;
for (int i = 0; i < m; i++) { //Chain forward star
int a, b;
cin >> a >> b;
edg[i].e = b;
edg[i].next = head[a];
head[a] = i;
in_degree[b]++;
}
queue<int> que;
for (int i = 1; i <= n; i++) {
if (in_edgree[i] == 0) {
que.push(i);
}
}
while (!que.empty()) {
int temp = que.front();
que.pop();
ans[cnt++] = temp;
if (cnt == n) {
for (int i = 1; i < n; i++) {
cout << ans[i] << " ";
}
cout << endl;
return 0;
}
for (int i = head[temp]; i != -1; i = edg[i].next) { //Traverse to find a new point with a penetration of 0
int e = edg[i].e;
in_degree[e]--;
if (in_degree[e] == 0) {
que.push(e);
}
}
}
cout << "have loop" << endl; //Ring
return 0;
}
Output all topology sorting
Permutation and combination
Number selection
Traversal edge, penetration - 1
recursion
Traversal edge, penetration + 1 (backtracking)
1. Deposit number
2. Mark de duplication
3. Traversal, penetration - 1
4. Recursion
5. Traversal, penetration - 1
6. Mark cancel
#include <iostream>
#include <vector>
using namespace std;
int n, m, ans[105], in_degree[105];
void func(int now, vector<vector<int> > &edg) {
if (now == n + 1) {
for (int i = 1; i <= n; i++) {
cout << ans[i] << " ";
}
cout << endl;
return ;
}
for (int i = 1; i <= n; i++) {
if (in_degree[i] == 0 && mark[i] == 0) {
ans[now] = i;
mark[i] = 1;
for (int j = 0; j < edg[i].size(); j++) {
in_degree[edg[i][j]]--;
}
func(now + 1, edg);
for (int j = 0; j < edg[i].size(); j++) {
in_degree[edg[i][j]]++;
}
mark[i] = 0;
}
}
}
int main() {
cin >> n >> m;
vector<vector<int> > edg(n + 1, vector<int>());
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
edg[a].push_back(b);
in_degree[b]++;
}
func(1, edg); // 1 recursion depth
return 0;
}
#641. Topology sorting
Title Description
Given a directed weighted graph with NN points and MM edges, we find its topological order. If there are multiple topological sorting, try to make the decimal number first and the large number last.
input
The first line of the input file is two integers nn and mm. Next, there are 22 integers a, Ba and B in the mm line, indicating that there is an edge from aa point to bb point to ensure that there is no ring in the data.
output
The output file contains 11 lines and a total of NN integers, indicating topological sorting. Each two numbers are separated by spaces.
sample input
7 6 1 2 1 4 2 3 4 5 3 6 5 6
sample output
1 2 3 4 5 6 7
code:
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
struct edge {
int e, next;
};
edge edg[100005];
int n, m, head[105], in_degreee[105], ans[105], cnt;
int main() {
memset(head, -1, sizeof(head));
cin >> n >> m;
for (int i = 0; i < m; i++) { //Chain forward star
int a, b;
cin >> a >> b;
edg[i].e = b;
edg[i].next = head[a];
head[a] = i;
in_degree[b]++;
}
queue<int> que;
for (int i = 1; i <= n; i++) {
if (in_edgree[i] == 0) {
que.push(i);
}
}
while (!que.empty()) {
int temp = que.front();
que.pop();
ans[cnt++] = temp;
if (cnt == n) {
for (int i = 1; i < n; i++) {
cout << ans[i] << " ";
}
cout << endl;
return 0;
}
for (int i = head[temp]; i != -1; i = edg[i].next) { //Traverse to find a new point with a penetration of 0
int e = edg[i].e;
in_degree[e]--;
if (in_degree[e] == 0) { // If the penetration is 0, update other points
que.push(e);
}
}
}
cout << "have loop" << endl; //Ring
return 0;
}
priority_queue<Type,Container,Functional>
Of which:
Type is the data type
Container is a container type (container must be a container implemented by array, such as vector, which is the default
Functional is the way of comparison, and it is also an important role for us to realize sorting later
When we do not declare any, the default is the large top heap
priority_queue<int, vector<int>, greater<int>> q;//Ascending order priority_queue<int, vector<int>, less<int>> q;//Descending order //greater and less are two pseudo functions implemented in std
neural network
Find the topological sort again, and find its C value
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
struct edge {
int e, v, next;
};
edge edg[10005];
int n, m, c[105], u[105], head[105], in_degree[105], out_degree[105], f;
int main() {
memset(head, -1, sizeof(head));
cin >> n >> m;
queue<int> que;
for (int i = 1; i <= n; i++) {
cin >> c[i] >> u[i];
if (c[i] != 0) {
que.push(i);
}
}
for (int i = 0; i < m; i++) {
int a, b, v;
cin >> a >> b >> v;
edg[i].e = b;
edg[i].v = v;
edg[i].next = head[a];
head[a] = i;
in_degree[b]++;
out_degree[a]++;
}
while (!que.empty()) {
int temp = que.front();
que.pop();
for (int i = head[temp]; i != -1; i = edg[i].next) {
int e = edg[i].e, v = edg[i].v;
in_degree[e]--;
if (c[temp] > 0) { //Excited state
c[e] += v * c[temp];
}
if (in_degree[e] == 0) {
que.push(e);
c[e] -= u[e];
}
}
}
for (int i = 1; i <= n; i++) {
if (out_degree[i] == 0 && c[i] > 0) {
cout << i << " " << c[i] << endl;
f = 1;
}
}
if (f == 0) {
cout << "NULL" << endl;
}
return 0;
}
Travel plan
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int n, m, in_degree[100005], ans[100005];
int main() {
cin >> n >> m;
vector <vector<int> > edg(n + 1, vector<int>());
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
edg[a].push_back(b);
in_degree[b]++;
}
queue<int> que;
for (int i = 1; i <= n; i++) {
if (in_degree[i] == 0) {
que.push(i);
ans[i] = 1;
}
}
while (!que.empty()) {
int temp = que.front();
que.pop();
for (int i = 0; i < edg[temp].size(); i++) {
int e = edg[temp][i];
ans[e] = ans[temp] + 1; //Previous point
in_degree[e]--;
if (in_degree[e] == 0) { // If the penetration is 0, update other points
que.push(e);
}
}
}
for (int i = 1; i <= n; i++) {
cout << ans[i] << endl;
}
return 0;
}
Food chain counting
The total number of output chains is essentially topological sorting
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int n, m, ans[5005], in_degree[5005], out_degree[5005];
int main() {
cin >> n >> m;
vector<vector<int> > edg(n + 1, vector<int>());
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
in_degree[b]++;
out_degree[a]++;
edg[a].push_back(b);
}
queue<int> que;
for (int i = 1; i <= n; i++) {
if (in_degree[i] == 0) {
que.push(i);
ans[i] = 1;
}
}
while (!que.empty()) {
int temp = que.front();
que.pop();
//for (int i =0; i < edg[temp].size(); i++) {
//int e = edg[temp][i];
for (auto e : edg[temp]) {
ans[e] += ans[temp]; //The sum of the number of chains to this
ans[e] %= 100000007;
in_degree[e]--;
if (in_degree[e] == 0) {
que.push(e);
}
}
}
int sum = 0;
for (int i = 1; i <= n; i++) {
if (out_degree[i] == 0) {
sum += ans[i];
sum %= 100000007;
}
}
cout << sum << endl;
return 0;
}
sort
Loop > solve
#include <iostream>
#include <vector>
#include <queue>
#include <cstdio>
using namespace std;
int n, m, in_degree[30];
char ans[30];
int func(vector<vector<int> > &edg) { //Ask for a round
int in[30];
queue<int> que;
for (int i = 0; i < n; i++) { //Copy in degree array
in[i] = in_degree[i];
if (in[i] == 0) {
que.push(i);
}
}
int ans_cnt = 0, mmax = que.size(); //ans_cnt has calculated the number of elements and tags
while (!que.empty()) { //If the number of mmax runs is greater than 1, it indicates that the topological sorting is not unique, so the sorting cannot be determined
mmax = max(mmax, (int)que.size());
int temp = que.front();
que.pop();
ans[ans_cnt++] = temp + 'A';
for (auto e : edg[temp]) {
in[e]--;
if (in[e] == 0) {
que.push(e);
}
}
}
if (ans_cnt != n) return -1;
if (mmax <= 1) return 1;
return 0;
}
int main() {
cin >> n >> m;
vector<vector<int> > edg(n, vector<int>());
for (int i = 1; i <= m; i++) {
char t[4];
cin >> t;
int a = t[0] - 'A', b = t[2] - 'A';
edg[a].push_back(b);
in_degree[b]++; //Penetration plus one
int cnt = func(edg);
if (cnt == -1) {
printf("Inconsistency found after %d relations.\n", i);
return 0;
} else if (cnt == 1) { //Topology sort unique
printf("Sorted sequence determined after %d relations: %s.", i, ans);
return 0;
}
}
printf("Sorted sequence cannot be determined.");
return 0;
}
Common questions and skills P3
First order, middle order and second order
Middle left right + left middle right - > left middle
#include <iostream>
#include <cstring>
using namespace std;
char front[105], mid[105];
void func(int fl, int fr, int ml, int mr) {
if (fl > fr) return ;
if (fl == fr) { //There is only one element Leaf node end recursion
cout << front[fl];
return ;
}
char root = front[fl];
int ind;
for (int i = ml; i <= mr; i++) {
if (mid[i] == root) {
ind = i; //Position of ind root
break;
}
}
// Original length mr - ml + 1
func(fl + 1, fl + ind - ml, ml, ind - 1); //Left subtree: start bit fl + 1, length ind - ml (including endpoint)
func(fl + ind - ml + 1, fr, ind + 1, mr); //Right subtree: start position fl + ind - ml + 1, end position fr length Mr - ind (including endpoint)
// Length mr - ml
cout << root;
}
int main() {
cin >> front >> mid;
func(0, strlen(front) - 1, 0, strlen(mid));
return 0;
}
Find the first order in the second order
Left and right middle + left middle right - > middle left
#include <iostream>
#include <cstring>
using namespace std;
char mid[105], back[105];
void func(int ml, int mr, int bl, int br) { //mid left mid right
if (ml > mr) return ;
if (ml == mr) { //There is only one element Leaf node end recursion
cout << mid[ml];
return ;
}
char root = back[br];
int ind;
for (int i = ml, i <= mr; i++) {
if (mid[i] == root) {
ind = i;
break;
}
}
cout << root
func(ml, ind - 1, nl, bl + ind - ml - 1);
func(ind + 1, mr, bl + ind - ml, br - 1);
}
int main() {
cin >> mid >> back;
func(0, strlen(mid) - 1, 0, strlen(back) - 1);
cout << endl;
return 0;
}
Constructing binary tree from preorder and inorder traversal sequences
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
unordered_map<int, int> m;
TreeNode *func(int fl, int fr, int ml, int mr, vector<int> &front, vector<int> &mid) {
if (fl > fr) return nullptr;
if (fl == fr) {
TreeNode *p = new TreeNode(front[fl]);
return p;
}
TreeNode *p = new TreeNode(front[fl]);
int ind = m[front[fl]];
p->left = func(fl + 1, fl + ind - ml, ml, ind - 1, front, mid);
p->right = func(fl + ind - ml + 1, fr, ind + 1, mr, front, mid);
return p;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
for (int i = 0; i < inorder.size(); i++) {
m[inorder[i]] = i;
}
TreeNode *root = func(0, preorder.size() - 1, 0, preorder.size() - 1, preorder, inorder);
return root;
}
};
Constructing binary tree by middle order and post order ergodic sequences
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
unordered_map<int, int> m;
TreeNode *func(int ml, int mr, int bl, int br, vector<int> &mid, vector<int> &back) {
if (ml > mr) return nullptr;
if (ml == mr) {
TreeNode *p = new TreeNode(mid[ml]);
return p;
}
TreeNode *p = new TreeNode(back[br]);
int ind = m[back[br]];
p->left = func(ml, ind - 1, bl, bl + ind - ml - 1, mid, back);
p->right = func(ind + 1, mr, bl + ind - ml, br - 1, mid, back);
return p;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
for (int i = 0; i < inorder.size(); i++) {
m[inorder[i]] = i;
}
TreeNode *root = func(0, inorder.size() - 1, 0, postorder.size() - 1, inorder, postorder);
return root;
}
};
How to judge that the given first order and middle order do not match
Find whether the traversal elements match in each recursion
[USACO06NOV]Roadblocks G
Strict secondary short circuit
bellmanford
#include <iostream>
#include <cstring>
#include <queue>
#include <cstdio>
using namespace std;
struct edge {
int e, v, next;
};
edge edg[200005];
int n, m, edg_cnt, head[5005], ans[5005], ans2[5005], mark[5005];
void add_edg(int s, int e, int v) {
edg[edg_cnt].e = e;
edg[edg_cnt].v = v;
edg[edg_cnt].next = head[s];
head[s] = edg_cnt++;
}
int main() {
memset(head, -1, sizeof(head));
memset(ans, 0x3f, sizeof(ans));
memset(ans2, 0x3f, sizeof(ans2));
cin >> n >> m;
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
add_edg(a, b, c);
add_edg(b, a, c);
if (a == 1 || b == 1) { // Secondary short circuit of all connection starting points
ans2[1] = min(ans2[1], c * 2); // The starting short circuit is updated to twice the shortest circuit (undirected graph)
}
}
ans[1] = 0;
queue<int> que;
que.push(1);
mark[1] = 1;
while (!que.empty()) {
int temp = que.front();
que.pop();
mark[temp] = 0;
for (int i = head[temp]; i != -1; i = edg[i].next) {
int e = edg[i].e, v = edg[i].v;
if (ans[temp] + v < ans[e]) { //Shortest - > shortest
ans2[e] = ans[e];
ans[e] = ans[temp] + v;
if (mark[e] == 0) {
mark[e] = 1;
que.push(e);
}
}
if (ans[temp] + v < ans2[e] && ans[temp] + v != ans[e]) { //Shortest circuit - > secondary short circuit
ans2[e] = ans[temp] + v;
if (mark[e] == 0) {
mark[e] = 1;
que.push(e);
}
}
if (ans2[temp] + v < ans2[e]) { //Sub short - > sub short
ans2[e] = ans2[temp] + v;
if (mark[e] == 0) {
mark[e] = 1;
que.push(e);
}
}
}
}
cout << ans2[n] << endl;
/*
for (int i = 1; i <= n; i++) {
cout << i << " " << ans[i] << " " << ans2[i] << endl;
}
*/
return 0;
}
Longest road
Bellman based on queue optimization_ ford
#include <iostream>
#include <cstring>
#include <queue>
#include <cstdio>
using namespace std;
struct edge {
int e, v, next;
};
edge edg[50005];
int n, m, head[1505], ans[1505], in_degree[1505], mark[1505];
int func(int x) { //For the first time, traverse all the edges of 1
if (x == n) return 0; //Can walk to
for (int i = head[x]; i != -1; i = edg[i].next) {
int e = edg[i].e;
if (mark[e] == 0) {
mark[e] = 1;
if (func(e) == 0) return 0; //Can walk to
}
}
return 1;
}
int main() {
memset(head, -1, sizeof(head));
cin >> n >> m;
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
edg[i].e = b;
edg[i].v = c;
edg[i].next = head[a];
head[a] = i;
in_degree[b]++;
}
if (func(1)) { //Judge whether you can go to point N
cout << -1 << endl;
return 0;
}
queue<int> que;
ans[1] = 0;
for (int i = 1; i <= n; i++) {
ans[i] = -2100000000; //Prevent negative numbers
if (in_degree[i] == 0) {
que.push(i);
}
}
ans[1] = 0;
while (!que.empty()) {
int temp = que.front();
que.pop();
for (int i = head[temp]; i != -1; i = edg[i].next) {
int e = edg[i].e, v = edg[i].v;
ans[e] = max(ans[e], ans[temp] + v);
in_degree[e]--;
if (in_degree[e] == 0) {
que.push(e);
}
}
}
cout << ans[n] << endl;
return 0;
}
Electricity competition in dormitory building
folyd
Multi source shortest path ranking
Determine the number of arrays before A + the number after A = = n - 1
#include <iostream>
#include <cstring>
using namespace std;
int n, m, arr[105][105], ans, in_degree[105];
int main() {
memset(arr, 0x3f, sizeof(arr));
cin >> n >> m;
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
arr[a][b] = 1;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= n; k++) {
arr[j][k] = min(arr[j][k], arr[j][i] + arr[i][k]);
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (arr[i][j] != 0x3f3f3f3f) { //Have path
in_degree[i]++; //The number of times i won
in_degree[j]++; //Behind, j lost
}
}
}
for (int i = 1; i <= n; i++) {
if (in_degree[i] == n - 1) {
ans++;
}
}
cout << ans << endl;
return 0;
}
Common questions and skills P4
Preorder traversal of binary tree
Non recursive traversal of binary tree: stack morois traversal (saving memory)
recursion
class Solution {
public:
void preorder(TreeNode *root, vector<int> &res) {
if (root == nullptr) {
return;
}
res.push_back(root->val);
preorder(root->left, res);
preorder(root->right, res);
}
vector<int> preorderTraversal(TreeNode *root) {
vector<int> res;
preorder(root, res);
return res;
}
};
stack iteration
vector
Stack the father into the stack, the left into the stack (recursive), the left is empty, the father out of the stack, the father right into the stack, the right is empty, the grandfather out of the stack
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
if (root == nullptr) {
return res;
}
stack<TreeNode*> stk;
TreeNode* node = root;
while (!stk.empty() || node != nullptr) {
while (node != nullptr) {
res.emplace_back(node->val); //Insert back
stk.emplace(node); //insert
node = node->left;
}
node = stk.top();
stk.pop();
node = node->right;
}
return res;
}
};
morois traversal
Find the precursor node and establish a virtual pointer. The right pointer traversed to the precursor is itself, indicating that after traversing the left subtree, root moves left and root moves right
Backtracking with null pointer
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> ans;
while (root != nullptr) {
if (root->left == nullptr) { //If the left subtree is empty, process the right subtree or return to the black edge
ans.push_back(root->val);
root = root->right;
} else {
TreeNode *pre = root->left;
while (pre->right != nullptr && pre->right != root) {//Looking for precursors
pre = pre->right;
}
if (pre->right == nullptr) { //Find the precursor for the first time, establish the black edge, and deal with the left subtree
ans.push_back(root->val);
pre->right = root;
root = root->left; //handle
} else { //Find the precursor for the second time, restore and process the right subtree
pre->right = nullptr;
root = root->right; //handle
}
}
}
return ans;
}
};
Middle order traversal of binary tree
morois traversal changes the output conditions
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> ans;
while (root != nullptr) {
if (root->left == nullptr) { //If the left subtree is empty, process the right subtree or return to the black edge
ans.push_back(root->val);
root = root->right;
} else {
TreeNode *pre = root->left;
while (pre->right != nullptr && pre->right != root) {//Looking for precursors
pre = pre->right;
}
if (pre->right == nullptr) { //Find the precursor for the first time, establish the black edge, and deal with the left subtree
//ans.push_ back(root->val); Change to output when the precursor is found for the second time
pre->right = root;
root = root->left; //handle
} else { //Find the precursor for the second time, restore and process the right subtree
ans.push_back(root->val);
pre->right = nullptr;
root = root->right; //handle
}
}
}
return ans;
}
};
Binary Tree Postorder Traversal
Reverse order output
class Solution {
public:
void add_ans(TreeNode *p, vector<int> &ans) {
stack<int> sta;
while (p != nullptr) {
sta.push(p->val);
p = p->right;
}
while (!sta.empty()) {
ans.push_back(sta.top());
sta.pop();
}
}
vector<int> postorderTraversal(TreeNode* root) {
vector<int> ans;
TreeNode *p = new TreeNode(0);
p->left = root;
while (p != nullptr) {
if (p->left == nullptr) {
p = p->right;
} else {
TreeNode *pre = p->left;
while (pre->right != nullptr && pre->right != p) {//Find precursor node
pre = pre->right;
}
if (pre->right == nullptr) { //Find the precursor for the first time, establish the black edge and deal with the left subtree
pre->right = p;
p = p->left;
} else { //Find the precursor for the second time, output in reverse order, and process the right subtree
pre->right = nullptr;
add_ans(p->left, ans); //Reverse order output
p = p->right;
}
}
}
return ans;
}
};
baseball game
class Solution {
public:
int calPoints(vector<string>& ops) { //string array
stack<int> sta;
int ans = 0;
for (auto s : ops) {
if (s == "+") {
int t1 = sta.top();
sta.pop();
int t2 = sta.top() + t1;
sta.push(t1);
sta.push(t2);
ans += t2;
} else if (s == "D") {
ans += sta.top() * 2;
sta.push(sta.top() * 2);
} else if (s == "C") {
ans -= sta.top();
sta.pop();
} else {
int t = stoi(s);
ans += t;
sta.push(t);
}
}
return ans;
}
};
Remove the outermost bracket
Use stack simulation to judge whether the stack is empty when entering and leaving the stack, so as to judge whether it is the outermost layer
class Solution {
public:
string removeOuterParentheses(string s) {
stack<bool> sta;
string ans;
for (auto c : s) {
if (c == '(') {
if (!sta.empty()) {
ans += '(';
}
sta.push(true);
} else {
sta.pop();
if (!sta.empty()) {
ans += ')';
}
}
}
return ans;
}
};
Number of recent requests
class RecentCounter {
public:
queue<int> que;
RecentCounter() {
}
int ping(int t) {
que.push(t);
while (t - que.front() > 3000) {
que.pop();
}
return que.size();
}
};
Same tree
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if (p == nullptr && q == nullptr) return true;
if (p == nullptr || q == nullptr || p->val != q->val) return flase;
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
};
Symmetric binary tree
class Solution {
public:
bool func(TreeNode *p, TreeNode *q) {
if (p == nullptr && q == nullptr) return true;
if (p == nullptr || q == nullptr || p->val != q->val) return false;
return func(p->left, q->right) && func(p->right, q->left);
}
bool isSymmetric(TreeNode* root) {
if (root == nullptr) return true;
return func(root->left, root->right);
}
};
Sequence traversal of binary tree
Wide search
class Solution {
public:
struct node {
TreeNode *p;
int deep; //Layer depth
};
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int> > ans;
if (root == nullptr) return ans;
vector<int> line;
int cnt = 0;
queue<node> que;
que.push((node){root, 0});
while (!que.empty()) {
node temp = que.front();
que.pop();
if (temp.deep != cnt) {
ans.push_back(line);
line.clear();
cnt = temp.deep;
}
line.push_back(temp.p->val);
if (temp.p->left != nullptr) {
que.push((node){temp.p->left, temp.deep + 1});
}
if (temp.p->right != nullptr) {
que.push((node){temp.p->right, temp.deep + 1});
}
}
ans.push_back(line); //Push on the last layer_ back
return ans;
}
};
Sequence traversal of binary tree II
1. Stack
2. Queue + reverse
class Solution {
public:
struct node {
TreeNode *p;
int deep; //Layer depth
};
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int> > ans;
if (root == nullptr) return ans;
vector<int> line;
int cnt = 0;
queue<node> que;
que.push((node){root, 0});
while (!que.empty()) {
node temp = que.front();
que.pop();
if (temp.deep != cnt) {
ans.push_back(line);
line.clear();
cnt = temp.deep;
}
line.push_back(temp.p->val);
if (temp.p->left != nullptr) {
que.push((node){temp.p->left, temp.deep + 1});
}
if (temp.p->right != nullptr) {
que.push((node){temp.p->right, temp.deep + 1});
}
}
ans.push_back(line); //Push on the last layer_ back
reverse(ans.begin(), ans.end());
return ans;
}
};
Zigzag sequence traversal of binary tree
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int> > ans; //ans[][]
if(root == nullptr) return ans;
queue<TreeNode*> q, next; //The two queues are divided into layers
vector<int> temp;
q.push(root);
while(!q.empty()) {
TreeNode *node = q.front();
q.pop();
temp.push_back(node->val);
if (node->left) next.push(node->left);
if (node->right) next.push(node->right);
if (q.empty()) {
ans.push_back(temp);
temp.clear();
q.swap(next);
}
}
for(int i = 0; i < ans.size(); i++) {
if(i % 2 == 1) {
std::reverse(ans[i].begin(), ans[i].end());
}
}
return ans;
}
};
Maximum depth of binary tree
class Solution {
public:
int ans;
void func(TreeNode *p, int deep) {
if (p == nullptr) return ;
ans = max(ans, deep);
func(p->left, deep + 1);
func(p->right, deep + 1);
}
int maxDepth(TreeNode* root) {
ans = 0;
func(root, 1);
return ans;
}
};
Minimum depth of binary tree
class Solution {
public:
int ans;
void func(TreeNode *p, int deep) {
if (p == nullptr || deep >= ans) return ;
if (p->left == nullptr && p->right == nullptr) {
ans = min(ans, deep);
return ;
}
func(p->left, deep + 1);
func(p->right, deep + 1);
}
int minDepth(TreeNode* root) {
if (root == nullptr) {
return 0;
}
ans = INT_MAX;
func(root, 1);
return ans;
}
};
Convert an ordered array to a binary search tree
class Solution {
public:
TreeNode* helper(vector<int>& nums, int left, int right) {
if (left > right) {
return nullptr;
}
int mid = (left + right) / 2;
TreeNode* root = new TreeNode(nums[mid]);
root->left = helper(nums, left, mid - 1);
root->right = helper(nums, mid + 1, right);
return root;
}
TreeNode* sortedArrayToBST(vector<int>& nums) {
return helper(nums, 0, nums.size() - 1);
}
};
Common skills P5
Segment tree
Segment tree interval and initialization O(N) modification O(logN) query O(logN)
Prefix and interval and initialization O(N) modify O(N) query O(1)
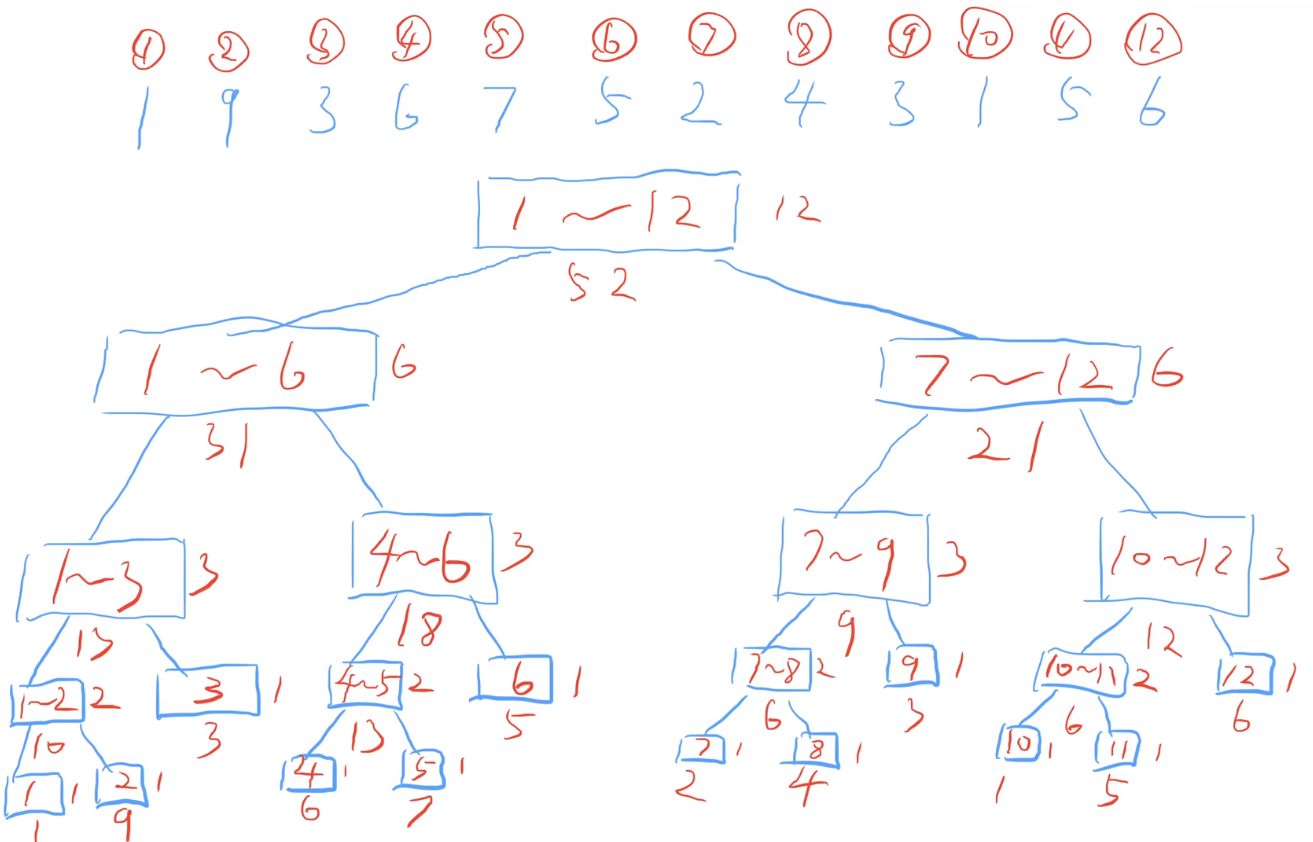
Segment tree modify tag
Exercise 2: segment tree template (2)
#include <iostream>
using namespace std;
struct node {
int l, r, cnt; // l~r interval, number of cnt elements
long long sum, lazy;
};
node tree[40005];
int n, m;
long long num[10005];
void up_sum(int now) { // Modified value floating up
tree[now].sum = tree[now * 2].sum + tree[now * 2 + 1].sum;
}
void down_lazy(int now) { //Lazy mark sinking
if (tree[now].lazy != 0) {
tree[now * 2].lazy += tree[now].lazy;
tree[now * 2].sum += tree[now * 2].cnt * tree[now].lazy;
tree[now * 2 + 1].lazy += tree[now].lazy;
tree[now * 2 + 1].sum += tree[now * 2 + 1].cnt * tree[now].lazy;
tree[now].lazy = 0;
}
}
void built_tree(int now, int l, int r) { //Build a tree
tree[now].l = l, tree[now].r = r;
tree[now].cnt = r - l + 1;
tree[now].lazy = 0;
if (l == r) {
tree[now].sum = num[l];
return ;
}
int mid = (l + r) / 2;
built_tree(now * 2, l, mid);
built_tree(now * 2 + 1, mid + 1, r);
up_sum(now);
}
void modify(int now, int l, int r, int v) { //modify
if (tree[now].l >= l && tree[now].r <= r) {
tree[now].sum += tree[now].cnt * v; // sum + = quantity * plus value
tree[now].lazy += v;
return ;
}
down_lazy(now);
int mid = (tree[now].l + tree[now].r) / 2;
if (mid >= l) modify(now * 2, l, r, v);
if (mid < r) modify(now * 2 + 1, l, r, v);
up_sum(now);
}
long long query(int now, int l, int r) { //query
if (tree[now].l >= l && tree[now].r <= r) {
return tree[now].sum;
}
down_lazy(now);
int mid = (tree[now].l + tree[now].r) / 2;
long long t = 0;
if (mid >= l) t += query(now * 2, l, r);
if (mid < r) t += query(now * 2 + 1, l, r);
return t;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> num[i];
}
built_tree(1, 1, n); //First floor 1 to n
for (int i = 0; i < m; i++) {
int t, a, b, c;
cin >> t;
if (t == 1) { //Modification plus c
cin >> a >> b >> c;
modify(1, a, b, c);
} else { //query
cin >> a >> b;
cout << query(1, a, b) << endl;
}
}
return 0;
}
Monotone stack
Ordered stack
It is suitable for solving the problem that the first element forward or backward is greater than or less than
The largest rectangle in the histogram
class Solution {
public:
struct node {
int ind, h; //ind subscript
};
int largestRectangleArea(vector<int>& heights) {
stack<node> sta; //up ascending order
sta.push((node){-1, -1});
int ans = 0;
for (int i = 0; i < heights.size(); i++) {
while (sta.size() != 1 && sta.top().h > heights[i]) { //Pop up and find the area of height[i]
node temp = sta.top();
sta.pop();
ans = max(ans, temp.h * (i - sta.top().ind - 1));
}
sta.push((node){i, heights[i]});
}
while (sta.size() != 1) {
node temp = sta.top();
sta.pop();
ans = max(ans, temp.h * ((int)heights.size() - sta.top().ind - 1));
}
return ans;
}
};
Similar to rainwater 42
Go shopping
The general second question in the written examination of previous years
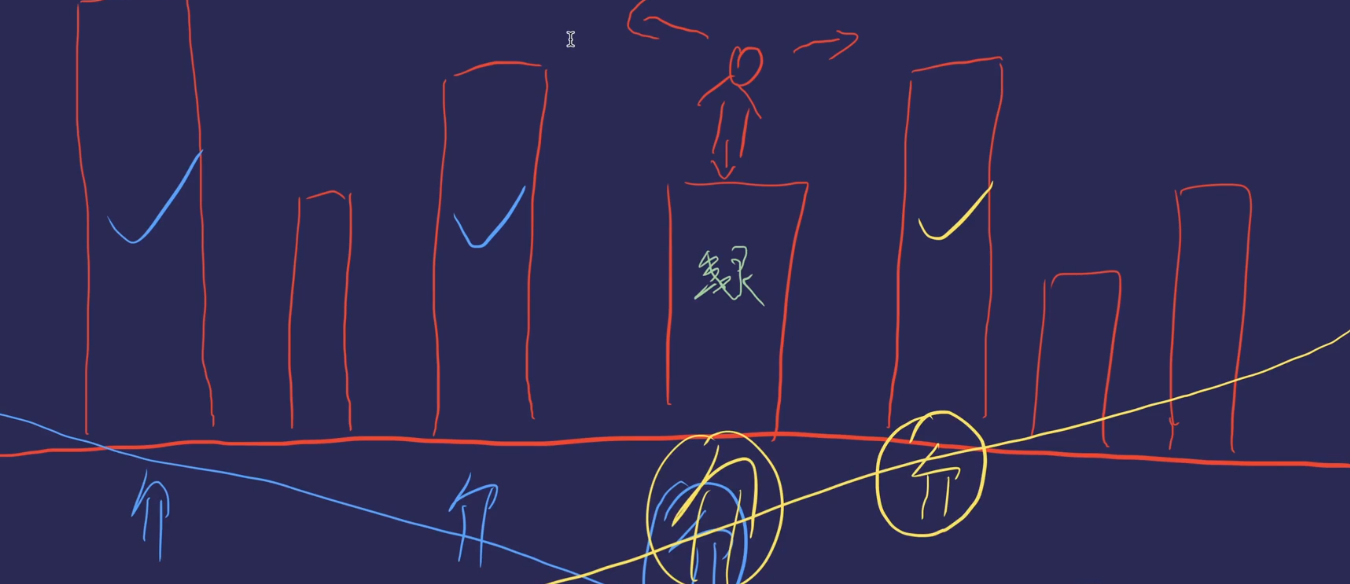
One person is the center, monotonically decreasing on the left and monotonically increasing on the right
Solution:
From left to right, find a monotonically decreasing stack (when the elements are not decreasing enough, the elements out of the stack will enter the stack again)
From right to left, find a monotonically decreasing stack
Monotone queue
Double ended queue, tail in, tail out
sliding window
Monotonically increasing queue minimum
Monotonically decreasing queue maximum
Title Description
Give an array with a length of NN, and a sliding window with a length of KK moves from the leftmost to the rightmost. Each time the window moves, as shown in the following figure:
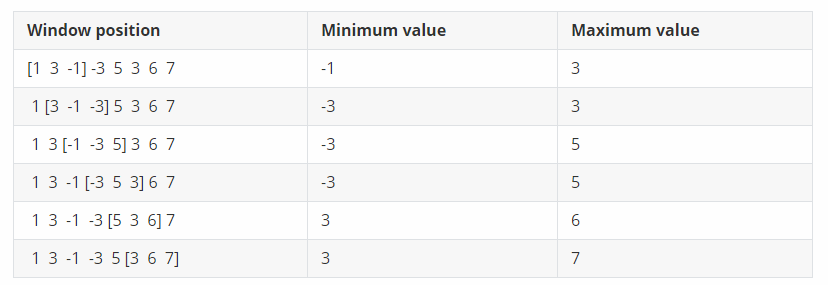
Find out the maximum and minimum values of the window in each position.
#include <iostream>
#include <deque>
using namespace std;
struct node {
int ind, val;
};
int n, k, num[300005], a1[300005], a2[300005];
int main() {
cin >> n >> k;
deque<node> mmin, mmax;
for (int i = 1; i <= n; i++) {
cin >> num[i];
while (!mmin.empty() && mmin.back().val > num[i]) { //Maintenance increment
mmin.pop_back();
}
mmin.push_back((node){i, num[i]});
if (mmin.front().ind + k <= i) { //Maintenance minimum
mmin.pop_front();
}
while (!mmax.empty() && mmax.back().val < num[i]) { //Maintenance decrement
mmax.pop_back();
}
mmax.push_back((node){i, num[i]});
if (mmax.front().ind + k <= i) { //Maintenance maximum
mmax.pop_front();
}
if (i >= k) { //Enter answer array
a1[i] = mmin.front().val;
a2[i] = mmax.front().val;
}
}
for (int i = k; i <= n; i++) {
if (i != k) cout << " ";
cout << a1[i];
}
cout << endl;
for (int i = k; i <= n; i++) {
if (i != k) cout << " ";
cout << a2[i];
}
cout << endl;
return 0;
}
Common problem solving skills P6
Dynamic programming DP
Recursive dynamic programming
1. Large problems can be decomposed into small problems (optimal substructure)
2. No aftereffect
method:
1. Observe that big problems can be decomposed into small problems
2. How is the status array defined
3. State transition equation
4. Initialization
Change
Greed is not tenable
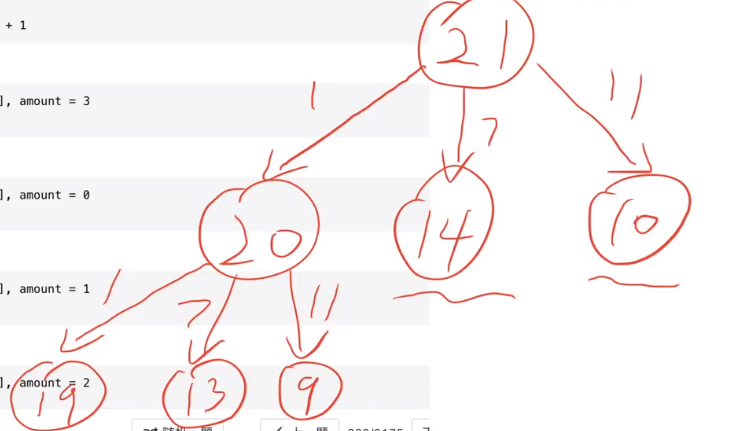
Recursive solution from 1 to 21
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> ans(amount + 1, INT_MAX / 2); //Initialize to INT_MAX / 2
ans[0] = 0;
for (int i = 1; i <= amount; i++) {
for (auto x : coins) {
if (i >= x) {
ans[i] = min(ans[i], ans[i - x] + 1);
}
}
}
if (ans[amount] == INT_MAX / 2) return -1;
return ans[amount];
}
};
raid homes and plunder houses
Max money from ans[x] to X
ans[i] = max(ans[i - 1], ans[i - 2] + nums[i - 1]);
class Solution {
public:
int rob(vector<int>& nums) {
vector<int> ans(nums.size() + 1, 0);
ans[1] = nums[0];
for (int i = 2; i <= nums.size(); i++) {
ans[i] = max(ans[i - 1], ans[i - 2] + nums[i - 1]);
}
return ans[nums.size()];
}
};
Longest increasing subsequence LIS
ans[x] the length of the longest increment sequence ending in X
ans[x] = max(ans[1] ~ ans[x]) + 1
Time complexity O(N^2)
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> ans(nums.size(), 1);
int mmax = 0;
for (int i = 0; i < nums.size(); i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
ans[i] = max(ans[i], ans[j] + 1);
}
}
mmax = max(mmax, ans[i]);
}
return mmax;
}
};
Time complexity O(NlogN)
Greedy thoughts
Maintain an ans array (the elements in the array are meaningless, and the array length is the desired length)
If you encounter a larger element, put it directly at the end
Otherwise, it is similar to replacing the previous element (finding the first one larger than it for replacement) / / 00001111
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> ans;
for (auto x : nums) {
if (ans.empty() || x > ans[ans.size() - 1]) {
ans.push_back(x);
} else {
//00001111
int l = 0, r = ans.size() - 1;
while (l != r) {
int mid = (l + r) / 2;
if (ans[mid] >= x) {
r = mid;
} else {
l = mid + 1;
}
}
ans[l] = x;
}
}
return ans.size();
}
};
Longest common subsequence LCS
Positive solution: ans[i][j] represents the longest common subsequence from 0 to I and from 0 to J
if (s1[i] == s[j]) ans[i][j] = 1 + ans[i - 1][j - 1]
else ans[i][j] = max(ans[i - 1][j], ans[i][j - 1])
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int n = text1.size(), m = text2.size();
vector<vector<int> > ans(n + 1, vector<int>(m + 1, 0));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (text1[i - 1] == text2[j - 1]) {
ans[i][j] = 1 + ans[i - 1][j - 1];
} else {
ans[i][j] = max(ans[i - 1][j], ans[i][j - 1]);
}
}
}
return ans[n][m];
}
};
Exercise 4: 0 / 1 Backpack
0 / 1 items can be taken once at most
ans[x][y] the maximum value that can be obtained by using the first X items to load the backpack with the upper limit of Y
anx[x - 1][y] no loading / no loading ans[x - 1][y] loading w[x] + ans[x - 1][y - v[x]] w[x] value v[x] space
This status of 0 / 1 backpack is based on the status of the first i - 1 pieces
#include <iostream>
using namespace std;
int n, v[105], w[105], ans[105][10005], m;
int main() {
cin >> m >> n;
for (int i = 1; i <= n; i++) {
cin >> v[i] >> w[i];
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) { //Traverse all spaces
if (v[i] <= j) {
ans[i][j] = max(ans[i - 1][j], w[i] + ans[i - 1][j - v[i]]); //Loaded with v[i], i - 1 item before removal. The upper limit is the maximum value of j-v[i]
} else {
ans[i][j] = ans[i - 1][j];
}
}
}
cout << ans[n][m] << endl;
return 0;
}
Scroll array
#include <iostream>
using namespace std;
int n, v[105], w[105], ans[10005], m;
int main() {
cin >> m >> n;
for (int i = 1; i <= n; i++) {
cin >> v[i] >> w[i];
}
for (int i = 1; i <= n; i++) // Traverse all items
for (int j = m; j >= v[i]; j--) //Traverse all spaces to load the i-th item
ans[j] = max(ans[j], w[i] + ans[j - v[i]]); //Scrolling array updates from back to front
cout << ans[m] << endl;
return 0;
}
Exercise 5: complete backpacking
Unlimited items
ans[x][y] the maximum value that can be obtained by using the first X items to load the backpack with the upper limit of Y
anx[x - 1][y] no loading / no loading ans[x - 1][y] loading w[x] + ans[x][y - v[x]] w[x] value v[x] space
The full knapsack state is based on the state of this layer
Scroll array from front to back
#include <iostream>
using namespace std;
int n, m, v[10005], w[10005], ans[10005];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> v[i] >> w[i];
}
for (int i = 1; i <= n; i++) // Traverse all items
for (int j = 1; j <= m; j++) //Traverse all spaces Load the i-th item
if(v[i] <= j)
ans[j] = max(ans[j], w[i] + ans[j - v[i]]); //The scrolling array is updated from front to back
cout << ans[m] << endl;
return 0;
}
Exercise 6: multiple backpacks
The number of items is limited
Divide the quantity to the power of 2 and reduce the number n to logn, such as 100 1 2 4 8 16 32
Problem converted to 0 / 1 knapsack problem
#include <iostream>
using namespace std;
int n, v[10005], w[10005], ans[10000005], m, cnt = 1;
int v1[105], w1[105], s1[105];
int main() {
cin >> m >> n;
for (int i = 1; i <= n; i++) {
cin >> v1[i] >> w1[i] >> s1[i];
}
for (int i = 1; i <= n; i++) {
int log = 1;
while (s1[i]) {
if (s1[i] < log) {
v[cnt] = v1[i] * s1[i];
w[cnt++] = w1[i] * s1[i];
s1[i] = 0;
} else {
v[cnt] = v1[i] * log;
w[cnt++] = w1[i] * log;
s1[i] -= log;
log *= 2;
}
}
}
cnt--;
for (int i = 1; i <= cnt; i++) // Traverse all items
for (int j = m; j >= v[i]; j--) //Traverse all spaces to load the i-th item
ans[j] = max(ans[j], w[i] + ans[j - v[i]]); //Scrolling array updates from back to front
cout << ans[m] << endl;
return 0;
}