3.3 Huffman tree

Basic concepts

Path length: the number of branches on the path between two nodes

External path length of the tree: the sum of the path length from each leaf node to the root node

Internal path length of the tree: the sum of the path length from each non leaf node to the root node

Weighted path length of tree: the sum of weighted path lengths of all leaf nodes in the tree

Huffman tree definition: it is a kind of tree with the shortest weighted path length

For example: find the weighted path length of the following binary tree

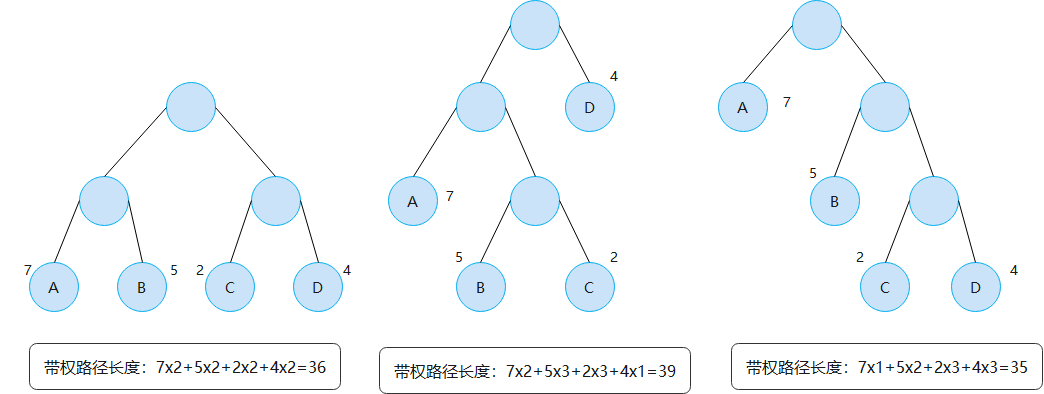
☑️ The depth of leaf nodes with large weight is small, and its cost relative to the total path length is the smallest. Therefore, if the weight of other leaf nodes is small, they will be pushed to the deeper part of the tree

Construction algorithm

❓ How to construct Huffman tree?

one ️⃣ According to the given n weights { w 1 , w 2 . . . , w n } \{w_1, w_2 ..., w_n\} {w1, w2..., wn}, construct a set of n binary trees F = { T 1 , T 2 , . . . , T n } F=\{T_1,T_2,...,T_n\} F={T1, T2,..., Tn}, where each binary tree contains only one with weight of w i w_i The root node of wi ， whose left and right subtrees are empty trees;

two ️⃣ In F, two binary trees with the smallest weight of their root node are selected as the left and right subtrees to construct a new binary tree, and the weight of the root node of the new binary tree is the sum of the weight of their left and right subtrees;

three ️⃣ Delete the two trees from F and add the newly generated new tree at the same time;

four ️⃣ (4) Repeat steps (2) and (3) until there is only one tree in F

Huffman coding

Prefix code

Code compiled using Huffman tree has prefix property prefix: any code in a group of codes is not the prefix of another code

This feature ensures that there are no multiple possibilities when the code string is de encoded

Character encoding

Using the characteristics of Huffman tree, unequal length coding is written for characters with different frequency, so as to shorten the length of the whole file

This is isinglass

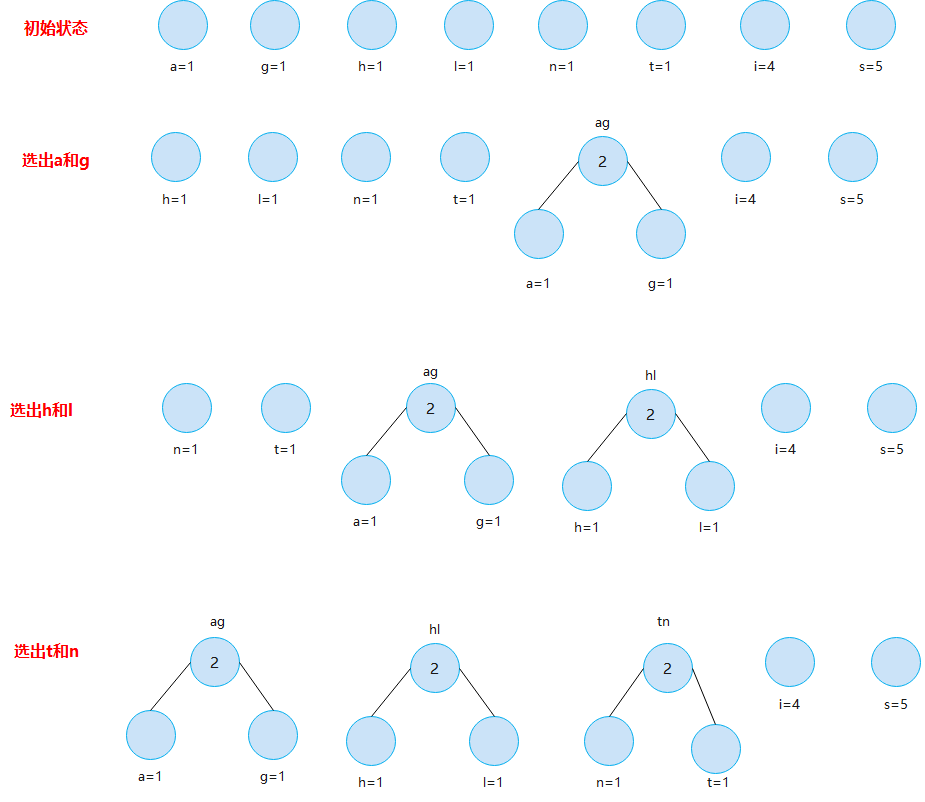
■ the frequency of t is 1, the frequency of H is 1, the frequency of I is 4, and the frequency of S is 5
■ the frequency of n is 1, the frequency of G is 1, the frequency of a is 1, and the frequency of I is 1

If the same length encoding form is adopted, the above eight letters need three binary encoding
Length = 15 * 3 = 45

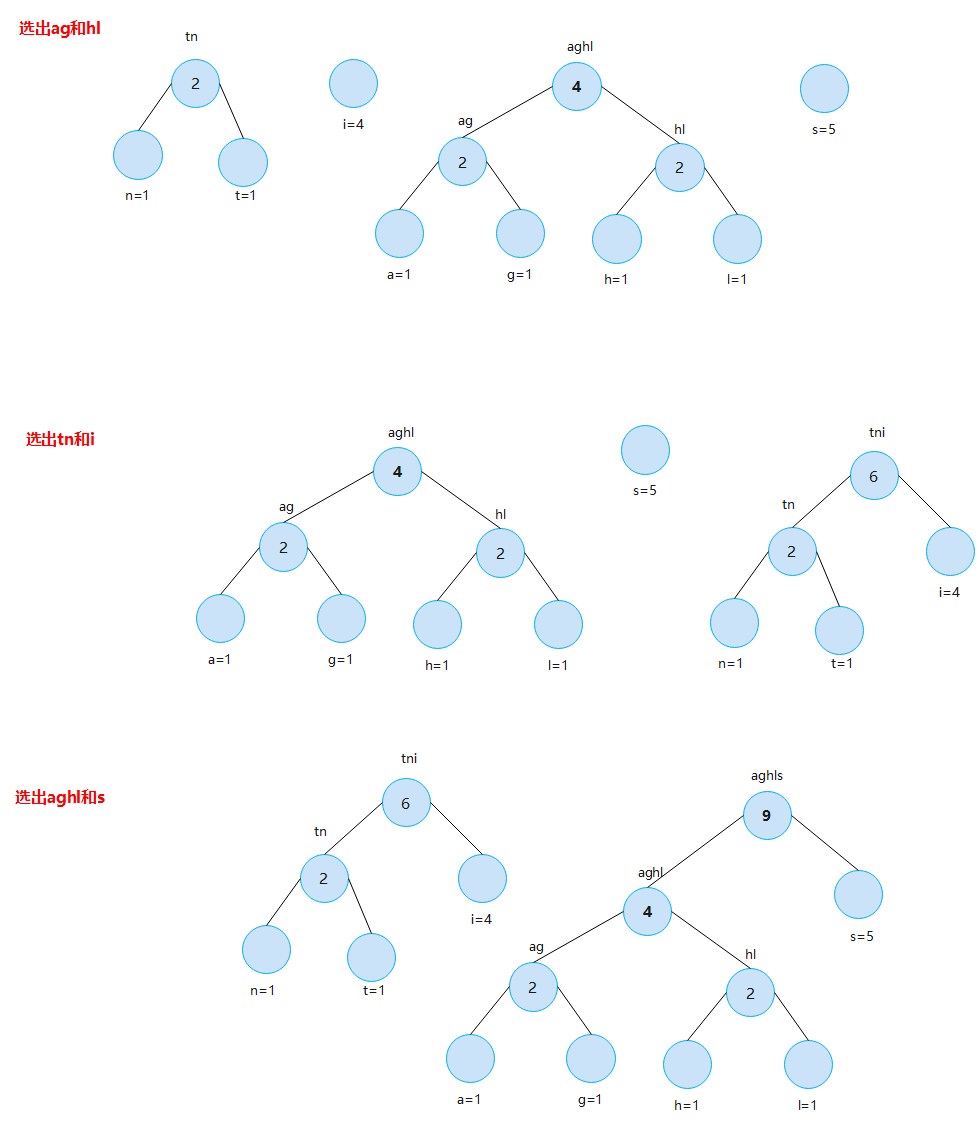
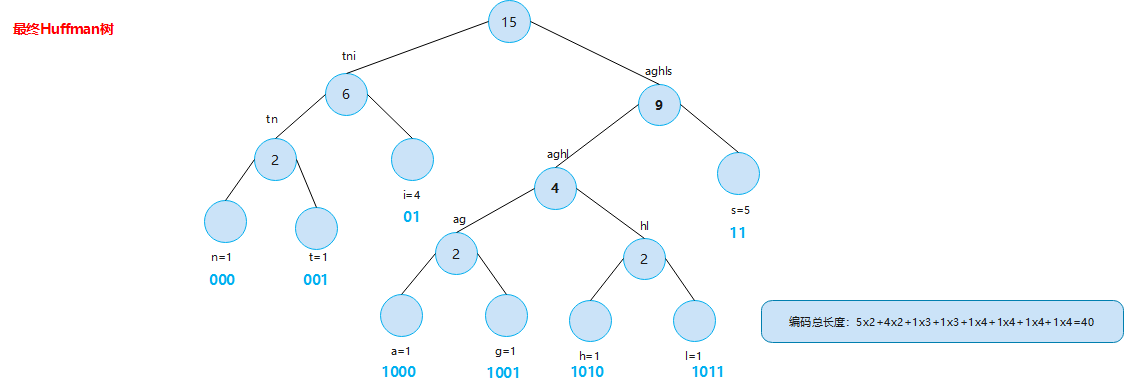
Create a Huffman tree according to the frequency of the letters above

graphic

Code implementation (java)

class Letter {
    char element;//letter
    double weight;//Frequency of letters

    public Letter(char element, double weight) {
        this.element = element;
        this.weight = weight;
    }

    public char getElement() {
        return element;
    }

    public void setElement(char element) {
        this.element = element;
    }

    public double getWeight() {
        return weight;
    }

    public void setWeight(double weight) {
        this.weight = weight;
    }
}

class HuffTreeNode {
    Letter letter;
    HuffTreeNode left;//Left child node
    HuffTreeNode right;//Right child node

    public Letter getLetter() {
        return letter;
    }

    public void setLetter(Letter letter) {
        this.letter = letter;
    }

    public HuffTreeNode getLeft() {
        return left;
    }

    public void setLeft(HuffTreeNode left) {
        this.left = left;
    }

    public HuffTreeNode getRight() {
        return right;
    }

    public void setRight(HuffTreeNode right) {
        this.right = right;
    }
}

public class HuffmanTree {
    //Simple bubble sorting
    private void sort(HuffTreeNode[] nodes) {
        int flags = 0;
        for (int i = 0; i < nodes.length-1; i++) {
            for (int j = 0; j < nodes.length-1-i; j++) {
                if (nodes[j].letter.weight > nodes[j + 1].letter.weight) {
                    HuffTreeNode temp = nodes[j];
                    nodes[j] = nodes[j + 1];
                    nodes[j + 1] = temp;
                    flags = 1;//If it is not ordered, set flags to 1;

                }
            }
            if (flags == 0)
                return;
        }
    }

    /**
     * Generate Huffman tree according to letters and their frequencies
     * @param letters
     * @return
     */
    public HuffTreeNode generateHuffTree(Letter[] letters) {
        HuffTreeNode[] nodes = new HuffTreeNode[letters.length];
        for (int i = 0; i < letters.length; i++) {
            nodes[i] = new HuffTreeNode();
            nodes[i].letter = letters[i];
        }
        while (nodes.length > 1) {
            sort(nodes);
            HuffTreeNode node1 = nodes[0];
            HuffTreeNode node2 = nodes[1];
            HuffTreeNode newTree = new HuffTreeNode();
            Letter temp = new Letter('0',node1.getLetter().getWeight()+node2.getLetter().getWeight());
            newTree.setLetter(temp);
            newTree.setLeft(node1);
            newTree.setRight(node2);
            HuffTreeNode[] nodes2 = new HuffTreeNode[nodes.length - 1];//New node array, length minus one
            for (int i = 2; i < nodes.length; i++) {
                nodes2[i - 2] = nodes[i];
            }
            nodes2[nodes2.length - 1] = newTree;
            nodes = nodes2;
        }
        return nodes[0];
    }

    /**
     * Postorder traversal
     * @param root Root node
     * @param code code
     */
    public void print(HuffTreeNode root,String code){
        if(root != null) {
            print(root.getLeft(),code+"0");
            print(root.getRight(),code+"1");
            if(root.getLeft() == null && root.getRight() == null) {
                String m=root.getLetter().getElement()+"frequency:"+root.getLetter().getWeight()+" Huffman code:"+code;
                System.out.println(m);
            }
        }
    }
    public static void main(String[] args) {
        Letter a = new Letter('a', 1);
        Letter g = new Letter('g', 1);
        Letter h = new Letter('h', 1);
        Letter l = new Letter('l', 1);
        Letter n = new Letter('n', 1);
        Letter t = new Letter('t', 1);
        Letter i = new Letter('i', 4);
        Letter s = new Letter('s', 5);
        Letter[] test = {a, g, h, l, n, t, i, s};
        HuffmanTree huffmanTree = new HuffmanTree();
        huffmanTree.print(huffmanTree.generateHuffTree(test),"");
    }
}

n frequency:1.0 Huffman code: 000
t frequency:1.0 Huffman code: 001
i frequency:4.0 Huffman code: 01
a frequency:1.0 Huffman code: 1000
g frequency:1.0 Huffman code: 1001
h frequency:1.0 Huffman code: 1010
l frequency:1.0 Huffman code: 1011
s frequency:5.0 Huffman code: 11

Non equal probability random number

Generate the corresponding random number according to the given probability
For example, there are six numbers: 1, 2, 3, 4, 5 and 6. Write a random generator to generate the corresponding six numbers according to the following probabilities (0.15, 0.20, 0.10, 0.30, 0.12 and 0.13)

one ️⃣ Solution 1: you can use the random number generation function in Java API to generate numbers between [0, 1) and generate numbers according to the interval

two ️⃣ Solution 2: use Huffman tree to reduce the number of comparisons

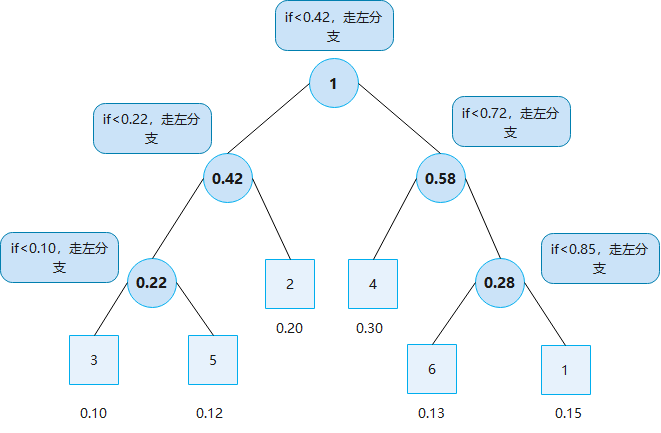
    public static int randomGenerate() {
        double temp = Math.random();
        int result=0;
        if (temp < 0.42) {
            if (temp < 0.22) {
                if (temp < 0.10) {
                    result = 3;
                } else {
                    result = 5;
                }
            } else {
                result = 2;
            }
        } else {
            if (temp < 0.72) {
                result = 4;
            } else {
                if (temp < 0.85) {
                    result = 6;
                } else {
                    result = 1;
                }
            }
        }
        return result;
    }