Add a line segment to the plane. Note that the label of the inserted line segment in article i is, and the two endpoints of the line segment are ( x 0 , y 0 ) , ( x 1 , y 1 ) (x_0,y_0),(x_1,y_1) (x0​,y0​),(x1​,y1​) .
Given a number k, query the number of the line segment with the largest intersection ordinate among the line segments intersecting the line x=k (if the intersection ordinates of multiple line segments and the query line are the largest, the line segment with the smallest number will be output). In particular, if no line segment intersects a given line, 0 is output;

For the above problem, the ordinary line segment tree is not easy to solve, so the Li Chao line segment tree is needed.

Li Chao line segment tree

We establish nodes like a segment tree, and each node maintains a line information (the dominant segment in a large range of the interval is not necessarily globally optimal).

Now let's assume that there are the following situations when we want to insert a straight line in an interval:
ps: the line inserted below is i n s ins Ins (green), the original line is n o w now now (red);

1. There is no line segment in this section. You can directly update the maximum line segment to the inserted line segment.

2. i n s ins The endpoints at both ends of the ins are smaller than n o w now If the endpoints at both ends of now are low, this situation can be returned directly because i n s ins This line segment will never be better than n o w now now is better.

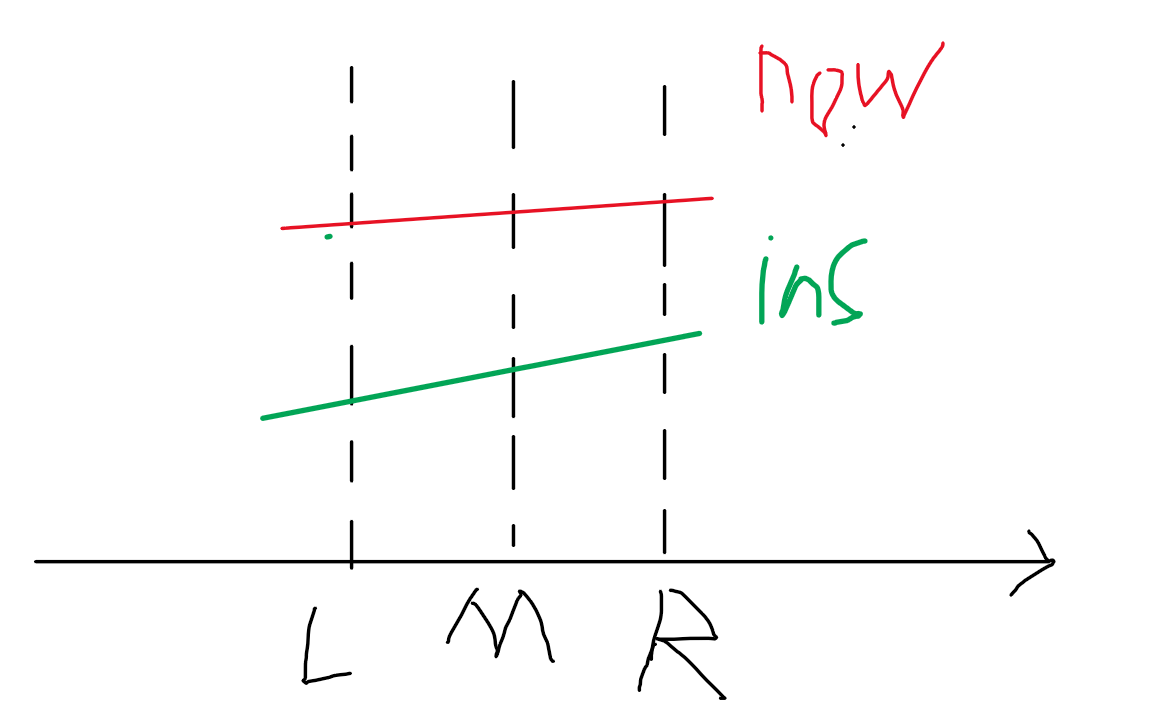
3. i n s ins The endpoints at both ends of the ins are smaller than n o w now The endpoints at both ends of now are high. In this case, directly modify the highest straight line in this interval (put n o w now Update now to i n s ins ins) can be returned.

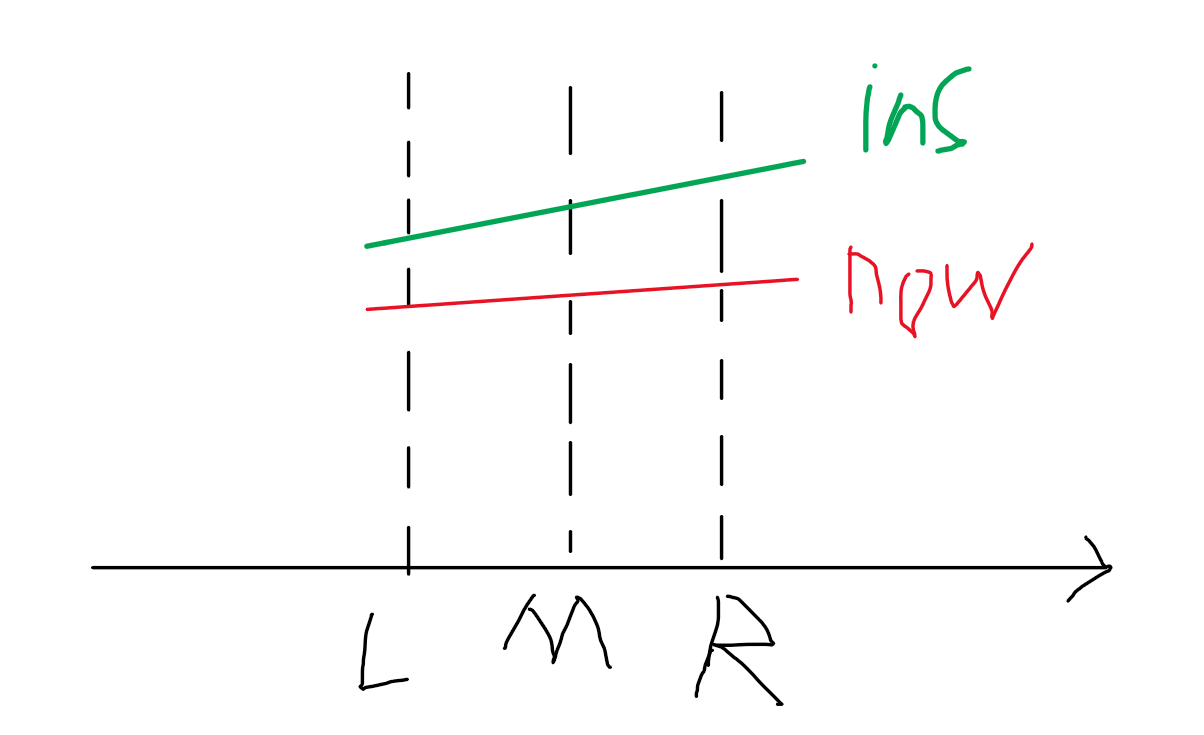
4. If the remaining two ends are inconsistent, special judgment shall be made:
① i n s ins The left endpoint of ins is greater than n o w now The left endpoint of now, i n s ins The right endpoint of ins is less than n o w now The right endpoint of now, and the intersection of the two line segments is on the left of the median in the interval.

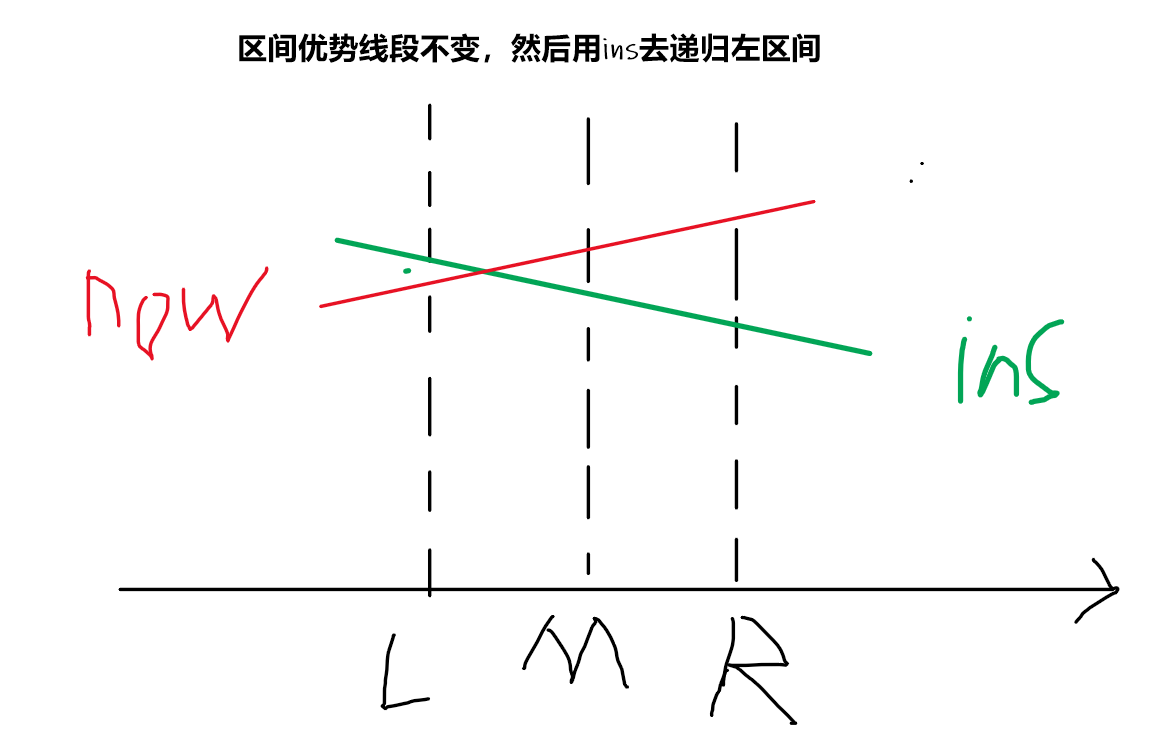
② i n s ins The left endpoint of ins is greater than n o w now The left endpoint of now, i n s ins The right endpoint of ins is less than n o w now The right endpoint of now, and the intersection of the two line segments is on the right of the median in the interval.

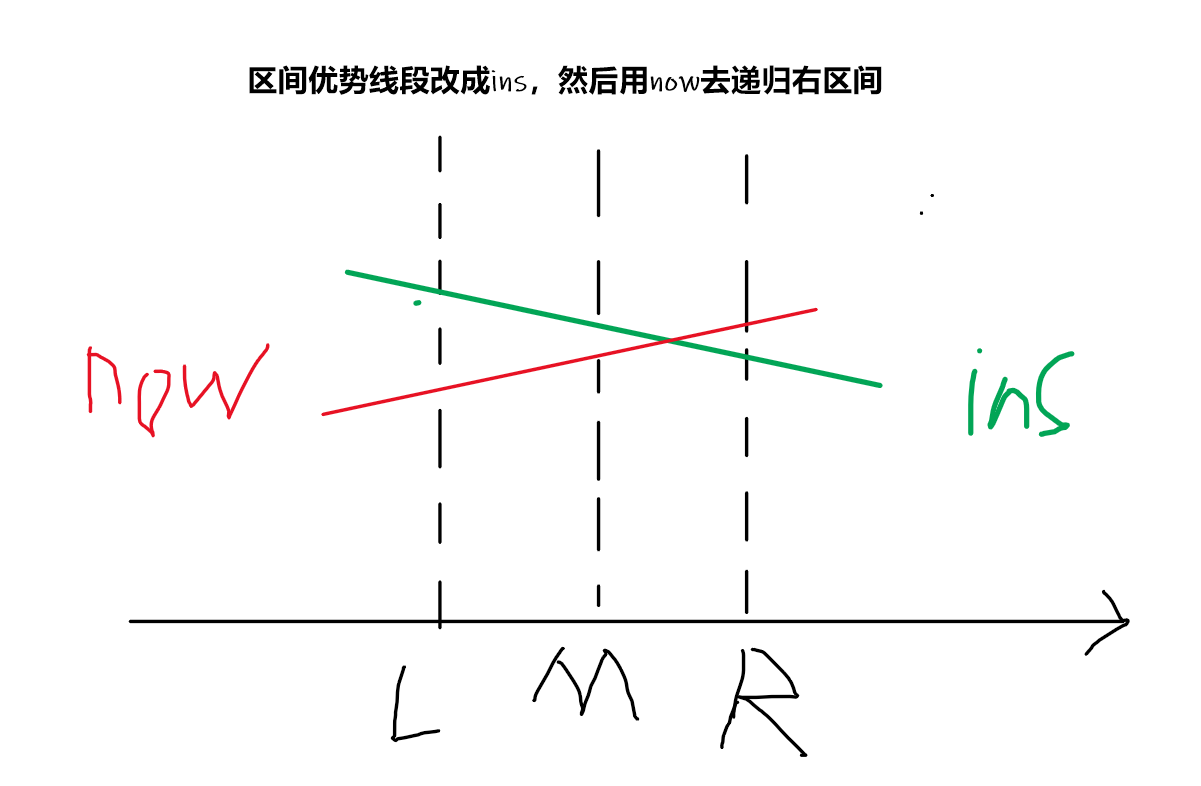
③ i n s ins The left endpoint of ins is less than n o w now The left endpoint of now, i n s ins The right endpoint of ins is greater than n o w now The right endpoint of now, and the intersection of the two line segments is on the left of the median in the interval.

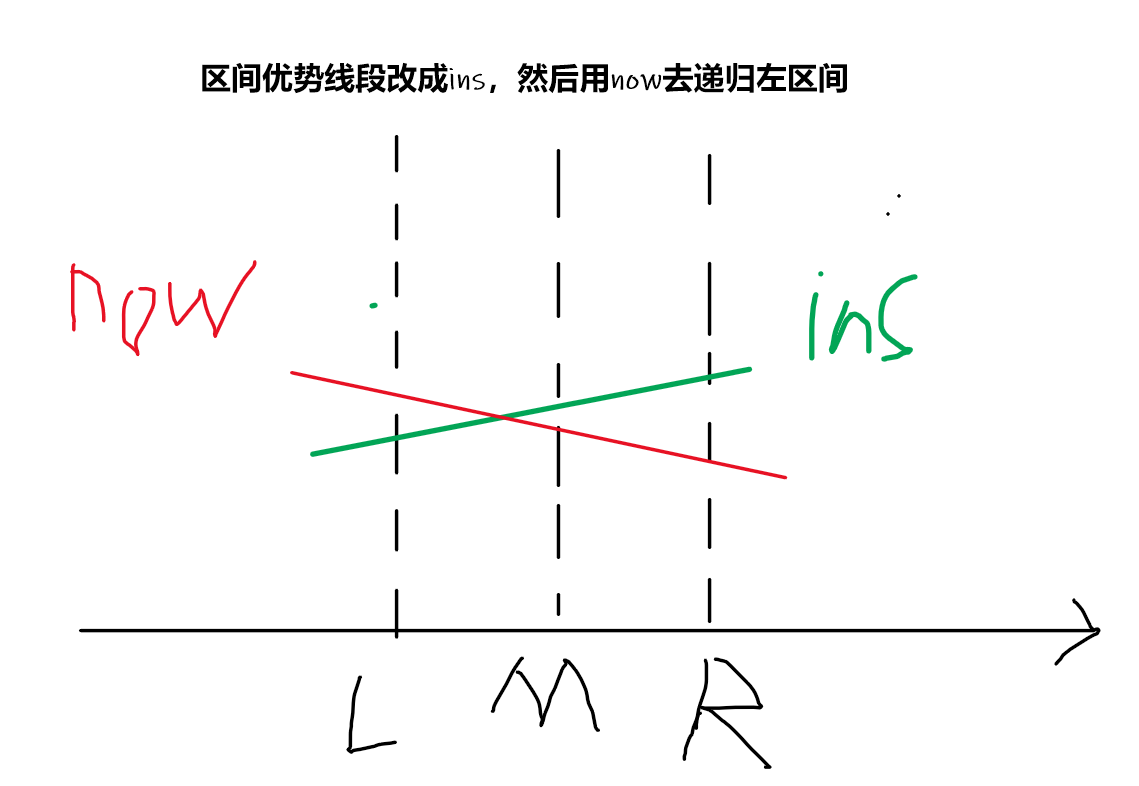
④ i n s ins The left endpoint of ins is less than n o w now The left endpoint of now, i n s ins The right endpoint of ins is greater than n o w now The right endpoint of now, and the intersection of the two line segments is on the right of the median in the interval.

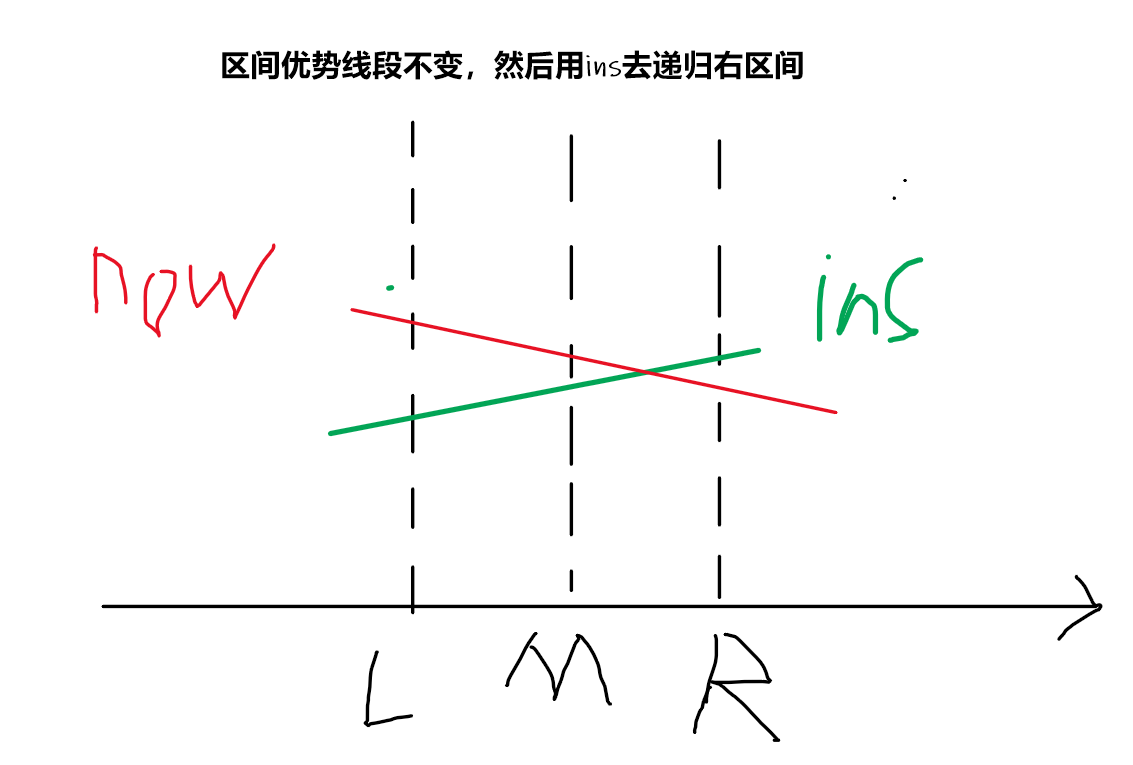
To sum up, Li Chao line segment tree is a line segment tree that maintains the line segment coverage in the plane with marker permanence. Unlike the line segment tree, the line maintained by the current node is not necessarily the best, but an advantageous line segment that can cover a larger area. Therefore, the query must be recursive to the end.

Next is the code implementation part (see below)
We know that for a straight line, it can be expressed as k x + b = y kx+b=y kx+b=y, so just remember k and b and we can represent a straight line.
Then there is the midpoint mentioned above. There are two algorithms:

1. Next, calculate the intersection of two straight lines directly, and then compare with the midpoint
2. Calculate the y at the midpoint of two straight lines for comparison.

The main thing is to draw the following picture by yourself, which will make the white point clearer.

#Define line pair < double, double > / / the first indicates K and the second indicates B
double f(line x,int X)//Calculate kx+b 
{
	return x.first*X+x.second; 
}
double inter(line x,line y)//Calculate intersection location
{
	return (y.second-x.second)/(x.first-y.first); 
}

Then there is the update operation. It is not difficult to understand the above situation analysis

int tot;//Counter
line li[N];//Record line information
int tree[N<<2];//Represents the possible optimal line segment of this node
void update(int now, int l, int r, int k, int L, int R)
{
	int mid = (l + r) >> 1;
	if (L <= l && r <= R)
	{
		if (!tree[now])//First case
		{
			tree[now] = k;
			return;
		}
		double ly1 = f(li[k], l), ry1 = f(li[k], r), ly2 = f(li[tree[now]], l), ry2 = f(li[tree[now]], r);
		//Calculate the y of the four endpoints of the two lines
		if (ly1 <= ly2 && ry1 <= ry2)return;
		//The second case
		if (ly1 >= ly2 && ry1 >= ry2) { tree[now] = k; return; }
		//The third case
		double in = inter(li[k], li[tree[now]]);
		//The fourth case
		if (ly1 >= ly2)
		{
			if (in <= mid)update(ls, l, mid, k, L, R);
			else update(rs, mid + 1, r, tree[now], L, R), tree[now] = k;
		}
		else
		{
			if (in > mid)update(rs, mid + 1, r, k, L, R);
			else update(ls, l, mid, tree[now], L, R), tree[now] = k;
		}
	}
	//If the interval to be changed is not reached, continue to recurse the line segment tree
	if (L <= mid)update(ls, l, mid, k, L, R);
	if (mid < R)update(rs, mid + 1, r, k, L, R);
}

Then there is the query operation. Because the following template question is to find the number of which line, my following example is to find the number.
If you want to find the size, you can use the following to find the number and calculate the y value. You can also record an mx array in the above line segment tree to represent the maximum value of the interval (see the second example for details)

int maxn(int x,int a,int b)//Calculation number
{
	return f(li[a],x)>f(li[b],x)?a:b;
}
int get(int now,int l,int r,int k)//To understand the meaning of mark permanence, instead of returning when an interval is found like an ordinary line segment tree, you should recurse to the end.
{
	int res=0;
	if(tree[now])res=maxn(k,res,tree[now]);
	if(l==r)return res;//special
	int mid=(l+r)>>1;
	if(k<=mid)res=maxn(k,res,get(ls,l,mid,k));
	else res=maxn(k,res,get(rs,mid+1,r,k));
	return res;
}

Examples

Template question

#include<bits/stdc++.h>
#define pll pair<int,int>
#define line pair<double,double>
#define mp make_pair
#define pb push_back
#define ll long long
#define INF 1e18
#define inf 0x3f3f3f3f
#define pi acos(-1)
#define db(x) cout<<x<<" "
#define dl(x) cout<<x<<endl
#define ls now<<1
#define rs now<<1|1
using namespace std;
const int mod = 1e9+7;
const int MAXN = 2e4 + 10;
const int N = 1e5 + 10;
const double eps =1e-6; 
int n, m;
int tot;
line li[N];
double f(line x,int X)
{
	return x.first*X+x.second; 
}
double inter(line x,line y)
{
	return (y.second-x.second)/(x.first-y.first); 
}
int tree[N<<2];

void add(int now,int l,int r,int k,int L,int R)
{
	int mid=(l+r)>>1;
	if(L<=l&&r<=R)
	{
		if(!tree[now])
		{
			tree[now]=k;
			return;
		}
		double ly1=f(li[k],l),ry1=f(li[k],r),ly2=f(li[tree[now]],l),ry2=f(li[tree[now]],r);
		if(ly1<=ly2&&ry1<=ry2)return;
		if(ly1>=ly2&&ry1>=ry2){tree[now]=k;return;}
		double in=inter(li[k],li[tree[now]]);
		if(ly1>=ly2)
		{
			if(in<=mid)add(ls,l,mid,k,L,R);
			else add(rs,mid+1,r,tree[now],L,R),tree[now]=k;
		}
		else
		{
			if(in>mid)add(rs,mid+1,r,k,L,R);
			else add(ls,l,mid,tree[now],L,R),tree[now]=k;
		}
	}
	if(L<=mid)add(ls,l,mid,k,L,R);
	if(mid<R)add(rs,mid+1,r,k,L,R); 
}
int maxn(int x,int a,int b)
{
	return f(li[a],x)>f(li[b],x)?a:b;
}
int get(int now,int l,int r,int k)
{
	int res=0;
	if(tree[now])res=maxn(k,res,tree[now]);
	if(l==r)return res;
	int mid=(l+r)>>1;
	if(k<=mid)res=maxn(k,res,get(ls,l,mid,k));
	else res=maxn(k,res,get(rs,mid+1,r,k));
	return res;
}
int ans;
int h(int k,int mod1)
{
	return (k+ans-1)%mod1+1;
}
void work()
{
 	cin>>n;
 	int M=39989;
 	for(int i=1;i<=n;i++)
 	{
 		int op;
		cin>>op;
		if(op)
		{
			int a,b,c,d;
			cin>>a>>b>>c>>d;
			a=h(a,M);c=h(c,M);b=h(b,1e9);d=h(d,1e9); 
			li[++tot]=(a==c?mp(.0,(double)max(b,d)):mp((d-b)*1.0/(c-a),(double)(b-(d-b)*1.0/(c-a)*a)));
			add(1,1,M,tot,min(a,c),max(a,c));
		}
		else
		{
			int k;cin>>k;
			k=h(k,M);
			ans=get(1,1,M,k);
			cout<<ans<<endl;
		}
	}
}
int main() {
	std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
	int _ = 1;
	//cin >> _;
	while (_--)work();
	return 0;
}

Tree section + Li Chao line segment tree

#include<bits/stdc++.h>
#define pll pair<int,int>
#define line pair<double,double>
#define mp make_pair
#define pb push_back
#define ll long long
#define INF 123456789123456789
#define inf 0x3f3f3f3f
#define pi acos(-1)
#define db(x) cout<<x<<" "
#define dl(x) cout<<x<<endl
#define ls now<<1
#define rs now<<1|1
using namespace std;
const int mod = 1e9+7;
const int MAXN = 2e5 + 10;
const int N = 1e5 + 10;
const double eps =1e-6;
int n, m;
struct node {
	int t, nex;
	ll len;
}e[MAXN];
int head[N], cnt;
void add(int a, int b, ll c)
{
	e[++cnt].len = c; e[cnt].nex = head[a]; e[cnt].t = b; head[a] = cnt;
}

ll dep[N], dis[N], siz[N],hson[N],fa[N],dft;
ll rnk[N], dfn[N], top[N];
void dfs1(int u,int f)
{
	siz[u] = 1;
	hson[u] = -1;
	for (int i = head[u]; i; i = e[i].nex)
	{
		int v = e[i].t;
		if (v == f)continue;
		dis[v] = dis[u] + e[i].len;
		dep[v] = dep[u] + 1;
		fa[v] = u;
		dfs1(v, u);
		siz[u] += siz[v];
		if (hson[u] == -1 || siz[v] > siz[hson[u]])hson[u] = v;
	}
}
void dfs2(int u,int t)
{
	dfn[u] = ++dft; rnk[dft] = u; top[u] = t;
	if (hson[u] != -1)dfs2(hson[u], t);
	for (int i = head[u]; i; i = e[i].nex)
	{
		int v = e[i].t;
		if (v == hson[u] || v == fa[u])continue;
		dfs2(v, v);
	}
}
int lca(int u, int v)
{
	ll f1 = top[u], f2 = top[v];
	while (f1!=f2)
	{
		if (dep[f1] < dep[f2])swap(f1, f2), swap(u, v);
		u = fa[f1]; f1 = top[u];
	}
	return dep[u] < dep[v]?u:v;
}

ll K[N << 2], B[N << 2];
int tot;
struct tr
{
	int l, r;
	int tag;
	ll mn;
}tree[N<<2];
ll get(int p, int u)
{
	return K[p]*dis[rnk[u]] + B[p];
}
void build(int now, int l, int r)
{
	tree[now].mn = INF, tree[now].tag = 1;
	tree[now].l = l, tree[now].r = r;
	if (l == r)return;
	int mid = (l + r) >> 1;
	build(ls, l, mid);
	build(rs, mid + 1, r);
}
void push_up(int now)
{
	tree[now].mn = min(tree[now].mn, min(tree[ls].mn, tree[rs].mn));
}
void update(int now, int l, int r, int p)
{
	int mid = (tree[now].l + tree[now].r) >> 1;
	int k = tree[now].tag;
	if (l <= tree[now].l && tree[now].r <= r)
	{
		ll ly1 = get(p, tree[now].l), ry1 = get(p, tree[now].r);
		ll ly2 = get(k, tree[now].l), ry2 = get(k, tree[now].r);
		if (ly1 >= ly2 && ry1 >= ry2)return;
		if (ly1 < ly2 && ry1 < ry2)
		{
			tree[now].tag = p;
			tree[now].mn = min(tree[now].mn, min(get(p, tree[now].l), get(p, tree[now].r)));
			return;
		}
		if (ly1 <= ly2)
		{
			if (get(p, mid) > get(k, mid))update(ls, l, r, p);
			else
			{
				update(rs, l, r, k);
				tree[now].tag = p;
			}
		}
		else
		{
			if (get(p, mid) > get(k, mid))update(rs, l, r, p);
			else
			{
				update(ls, l, r, k);
				tree[now].tag = p;
			}
		}
		tree[now].mn = min(tree[now].mn, min(get(tree[now].tag, tree[now].l), get(tree[now].tag, tree[now].r)));
		push_up(now);
		return;
	}
	if (l <= mid)update(ls, l, r, p);
	if (mid < r)update(rs,l, r, p);
	push_up(now);
}
ll query(int now, int l, int r)
{
	if (l <= tree[now].l && tree[now].r <= r)return tree[now].mn;
	ll ans = min(get(tree[now].tag, max(l, tree[now].l)), get(tree[now].tag, min(r, tree[now].r)));
	int mid = (tree[now].l + tree[now].r) >> 1;
	if (l <= mid)ans = min(ans, query(ls, l, r));
	if (mid < r)ans = min(ans, query(rs, l, r));
	return ans;
}
void op1(int u, int v, int k)
{
	int f1 = top[u], f2 = top[v];
	while (f1 != f2)
	{
		update(1, dfn[f1], dfn[u], k);
		u = fa[f1]; f1 = top[u];
	}
	update(1, dfn[v], dfn[u], k);
}
ll op2(int u, int v)
{
	int f1 = top[u], f2 = top[v];
	ll res = INF;
	while (f1 != f2)
	{
		if (dep[f1] < dep[f2])swap(f1, f2), swap(u, v);
		res=min(res,query(1, dfn[f1], dfn[u]));
		u = fa[f1]; f1 = top[u];
	}
	if (dep[u] < dep[v])swap(f1, f2), swap(u, v);
	res = min(res, query(1, dfn[v], dfn[u]));
	return res;
}
void work()
{
	cin >> n >> m;
	for (int i = 1; i < n; i++)
	{
		ll a, b, c;
		cin >> a >> b >> c;
		add(a, b, c); add(b, a, c);
	}

	dfs1(1,0);
	dfs2(1, 1);
	B[++tot] = INF; K[tot] = 0;
	build(1, 1, n);

	for (int i = 1; i <= m; i++)
	{
		int op;
		cin >> op;
		if (op == 1)
		{
			int s, t;
			ll a, b;
			cin >> s >> t >> a >> b;
			int lc = lca(s, t);//It is mainly the processing of two K B here
			//cout << lc << endl;
			K[++tot] = -a; B[tot] = b + a * dis[s];
			op1(s, lc, tot);
			K[++tot] = a; B[tot] = b + a * dis[s] - a* 2 * dis[lc];
			op1(t, lc, tot);
		}
		else
		{
			int l, r;
			cin >> l >> r;
			cout << op2(l, r) << endl;
		}
	}
}
int main() {
	std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
	int _ = 1;
	//cin >> _;
	while (_--)work();
	return 0;
}