hash and ordered table

unordered_set usage
unordered_map usage (the same as the map usage, but the map is orderly, which is out of order) -- algorithm note 6.4
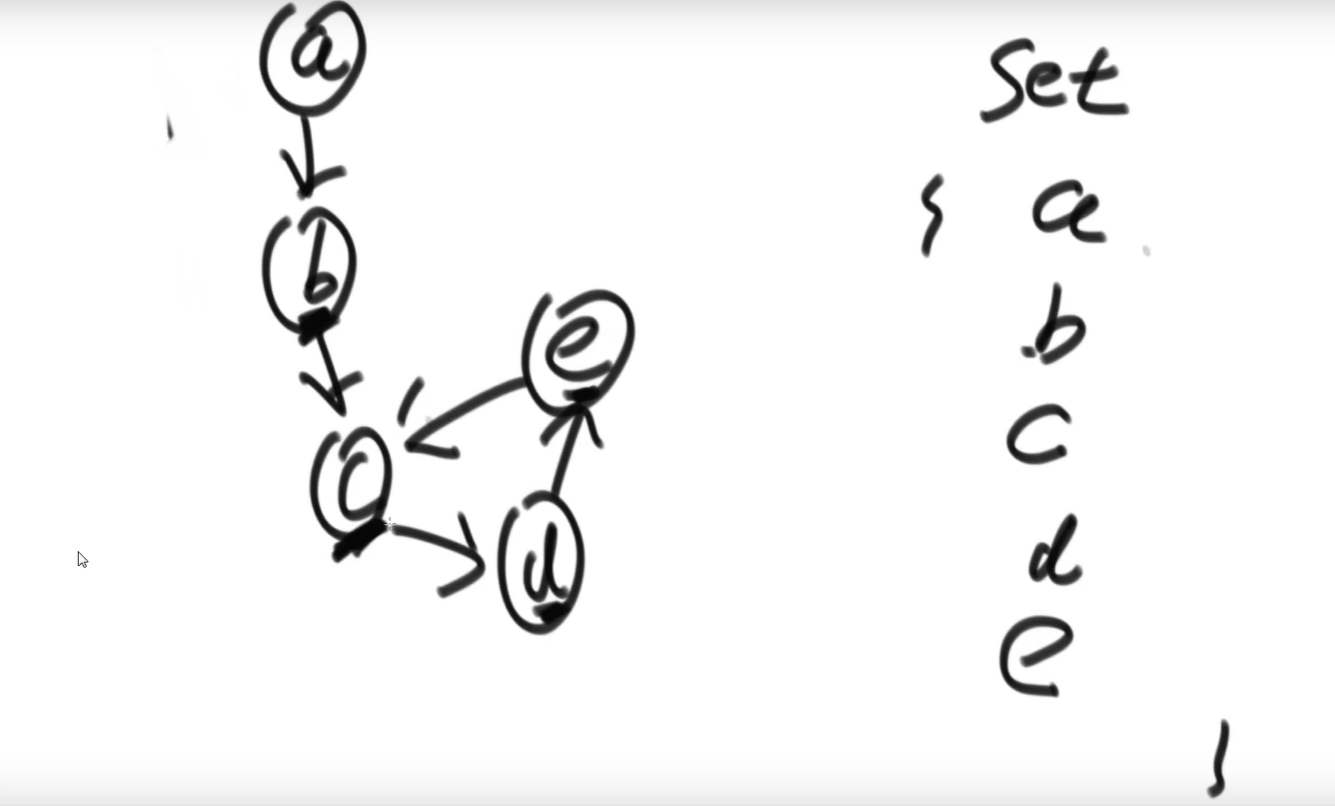
Ordered tables are Set and Map
No matter how many records are put in the hash table, the time is complex, and love is a constant level.
Linked list


Note: the adjustment of the linked list may have the operation of changing the header, so it will bring the return value. If the header is not changed, it can be defined as void type.

In fact, this problem is similar to the following figure. In external sorting, use two pointers to point to the two linked lists. Who is smaller and who moves to the right. When equal, put value into a new array and move together. One of them crossed the line and stopped.
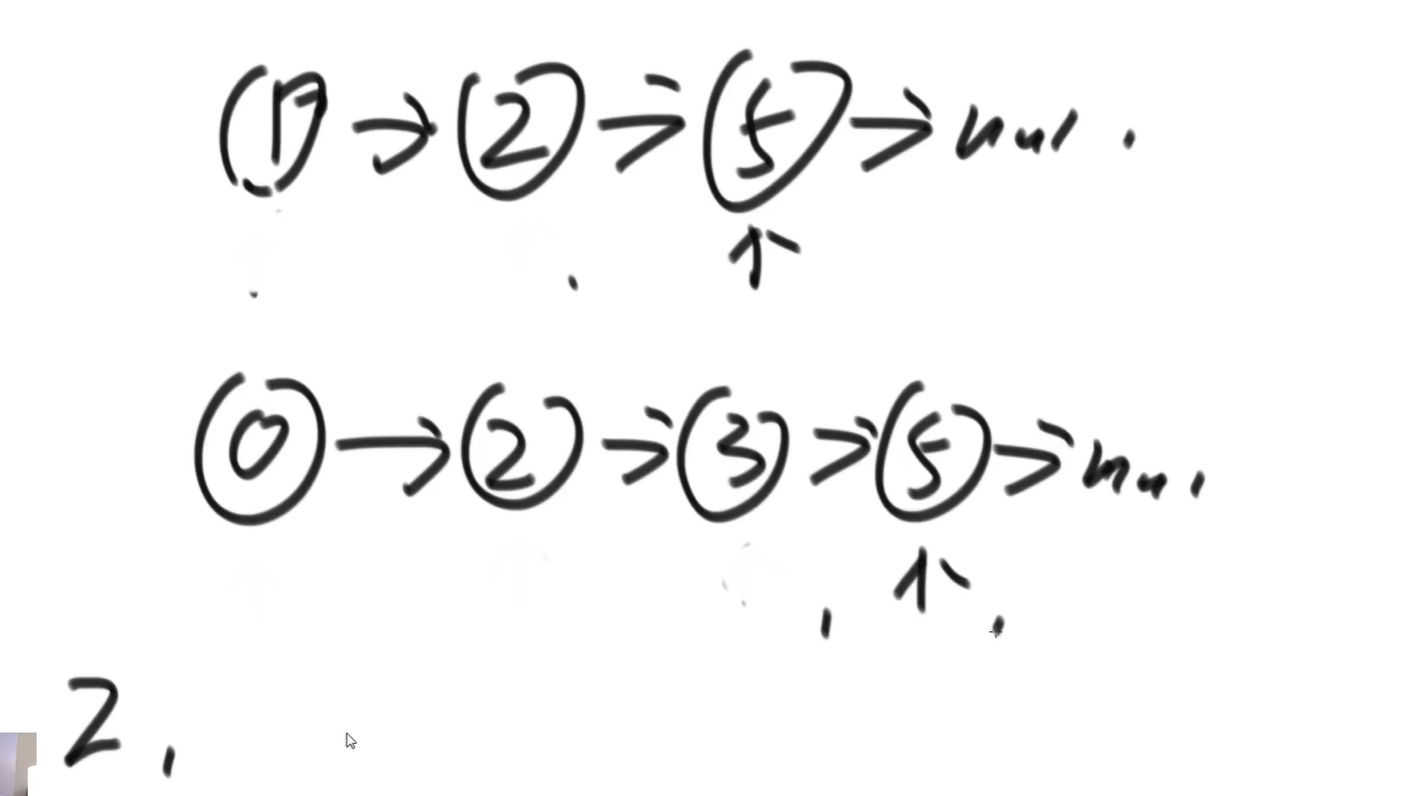


Written test: just put it directly in the stack
The stack comes in first and then out. After putting it in, it pops out upside down. It's different from the original linked list.
More space saving: put the right part of the linked list on the stack, and then pop it up. Compare it with the original linked list from the beginning.
This method uses the fast and slow pointer (an important skill) to find the midpoint.
Fast and slow pointer: the fast pointer takes two steps at A time, and the slow pointer takes one step at A time. When the fast pointer is finished, the slow pointer comes to the midpoint. Then, when traversing down the midpoint, reverse the order, point to the empty midpoint, and point back to the rest. As shown in the figure below, A and B go to the middle at the same time, compare each step, and stop when one goes to the empty. Finally, restore the right part of the linked list to normal, and then return true/false.

The speed pointer needs to be customized: boundary conditions
//Stack code only
struct ListNode {
int val;
struct ListNode *next;
};
class Solution {
public:
bool isPail(ListNode* head) {
// write code here
stack<int> st;
ListNode* cur = head;
while(cur != NULL)
{
st.push(cur->val);
cur = cur->next;
}
while(head != NULL)
{
if(head->val != st.top()){
return false;
}
st.pop();
head = head->next;
}
return true;
}
};
//n/2
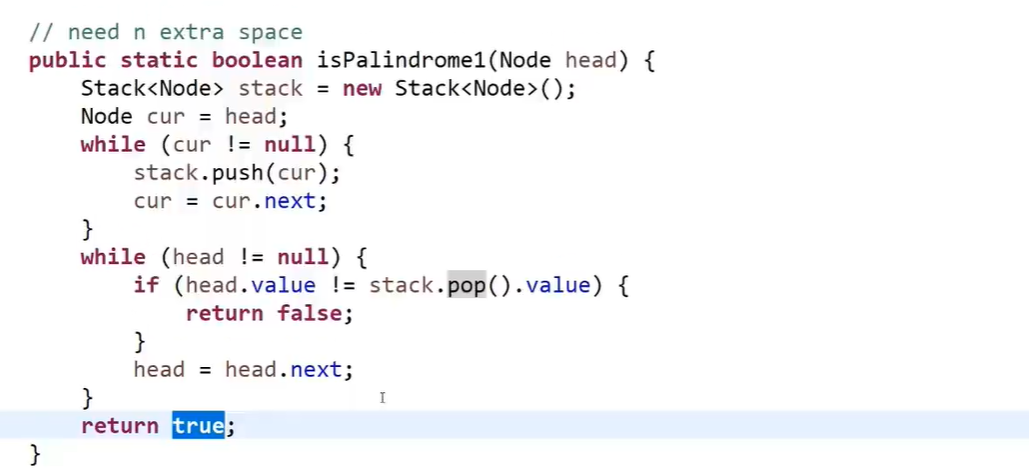
// need n/2 extra space
public static boolean isPalindrome2(Node head) {
if (head == null || head.next == null) {
return true;
}
Node right = head.next;
Node cur = head;
while (cur.next != null && cur.next.next != null) {
right = right.next;
cur = cur.next.next;
}
Stack<Node> stack = new Stack<Node>();
while (right != null) {
stack.push(right);
right = right.next;
}
while (!stack.isEmpty()) {
if (head.value != stack.pop().value) {
return false;
}
head = head.next;
}
return true;
}
//Speed pointer
// need O(1) extra space
public static boolean isPalindrome3(Node head) {
if (head == null || head.next == null) {
return true;
}
Node n1 = head;
Node n2 = head;
while (n2.next != null && n2.next.next != null) { // find mid node
n1 = n1.next; // n1 -> mid
n2 = n2.next.next; // n2 -> end
}
n2 = n1.next; // n2 -> right part first node
n1.next = null; // mid.next -> null
Node n3 = null;
while (n2 != null) { // right part convert
n3 = n2.next; // n3 -> save next node
n2.next = n1; // next of right node convert
n1 = n2; // n1 move
n2 = n3; // n2 move
}
n3 = n1; // n3 -> save last node
n2 = head;// n2 -> left first node
boolean res = true;
while (n1 != null && n2 != null) { // check palindrome
if (n1.value != n2.value) {
res = false;
break;
}
n1 = n1.next; // left to mid
n2 = n2.next; // right to mid
}
n1 = n3.next;
n3.next = null;
while (n1 != null) { // recover list
n2 = n1.next;
n1.next = n3;
n3 = n1;
n1 = n2;
}
return res;
}
Title: a group of numbers. Sort them. Those less than a certain number are on the left and those greater than a certain number are on the right.

Set 6 parameters
SH
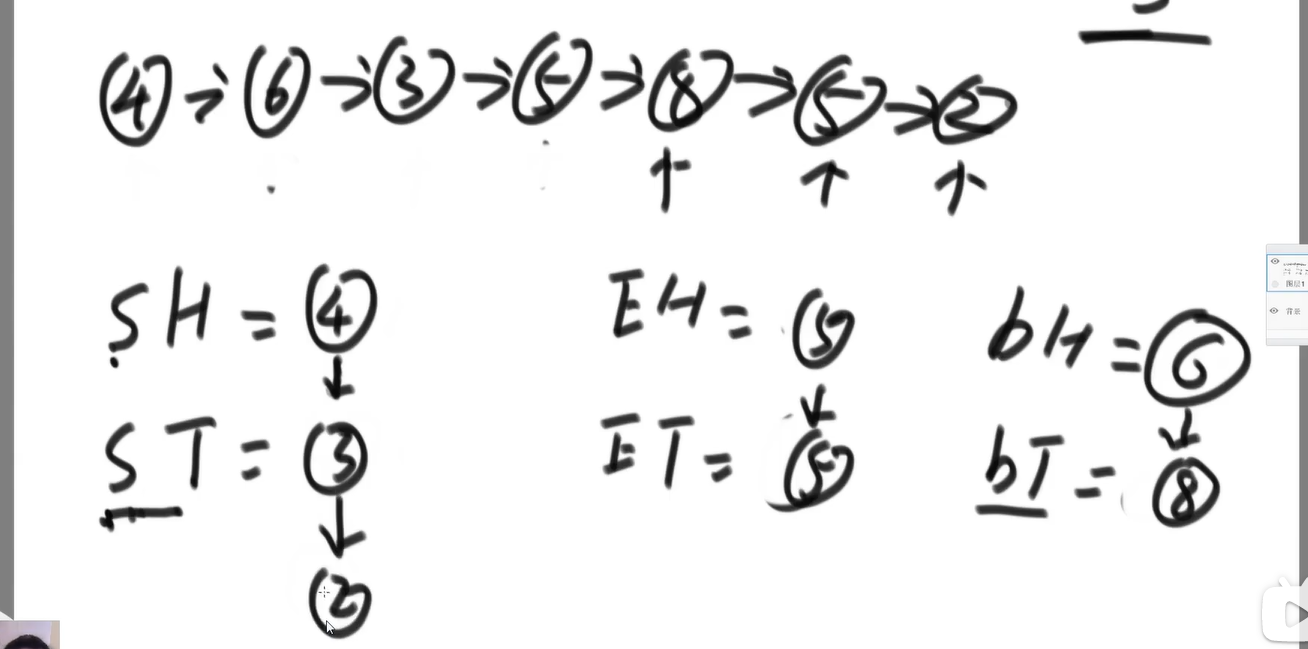
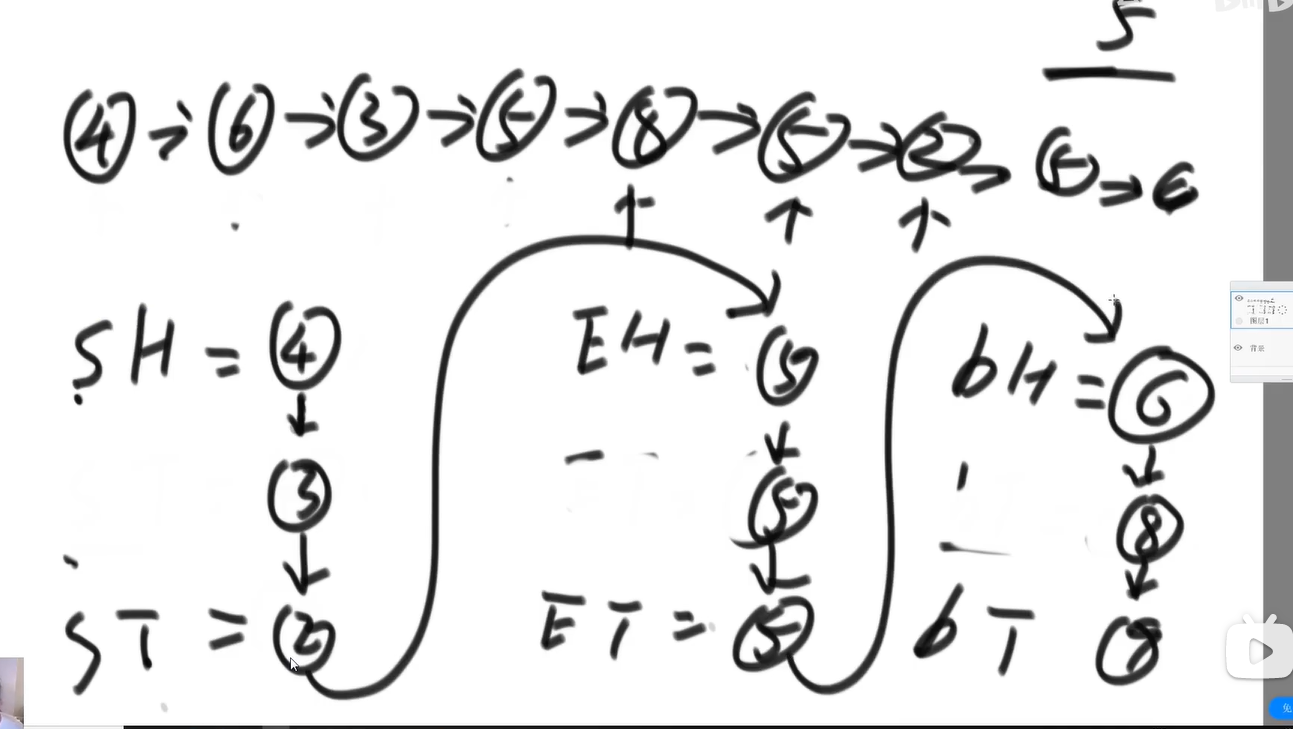
Finally, when connecting, pay attention to the discussion boundary. For example, if there is no number less than 5, an error will be reported if the null pointer points to a number equal to 5
public static Node listPartition2(Node head, int pivot) {
Node sH = null; // small head
Node sT = null; // small tail
Node eH = null; // equal head
Node eT = null; // equal tail
Node bH = null; // big head
Node bT = null; // big tail
Node next = null; // save next node
// every node distributed to three lists
while (head != null) {
next = head.next;
head.next = null;
if (head.value < pivot) {
if (sH == null) {//If it is the first node
sH = head;//Set the head and tail less than the area
sT = head;
} else {//Not the first node
sT.next = head;//Connect the next pointer of the old tail to the current node
sT = head;//The current node becomes the new tail of the old region
}
} else if (head.value == pivot) {
if (eH == null) {
eH = head;
eT = head;
} else {
eT.next = head;
eT = head;
}
} else {
if (bH == null) {
bH = head;
bT = head;
} else {
bT.next = head;
bT = head;
}
}
head = next;
}
// small and equal reconnect
if (sT != null) {
sT.next = eH;
eT = eT == null ? sT : eT;
}
// all reconnect
if (eT != null) {
eT.next = bH;
}
return sH != null ? sH : eH != null ? eH : bH;
}

//With extra space, the hash table is solved
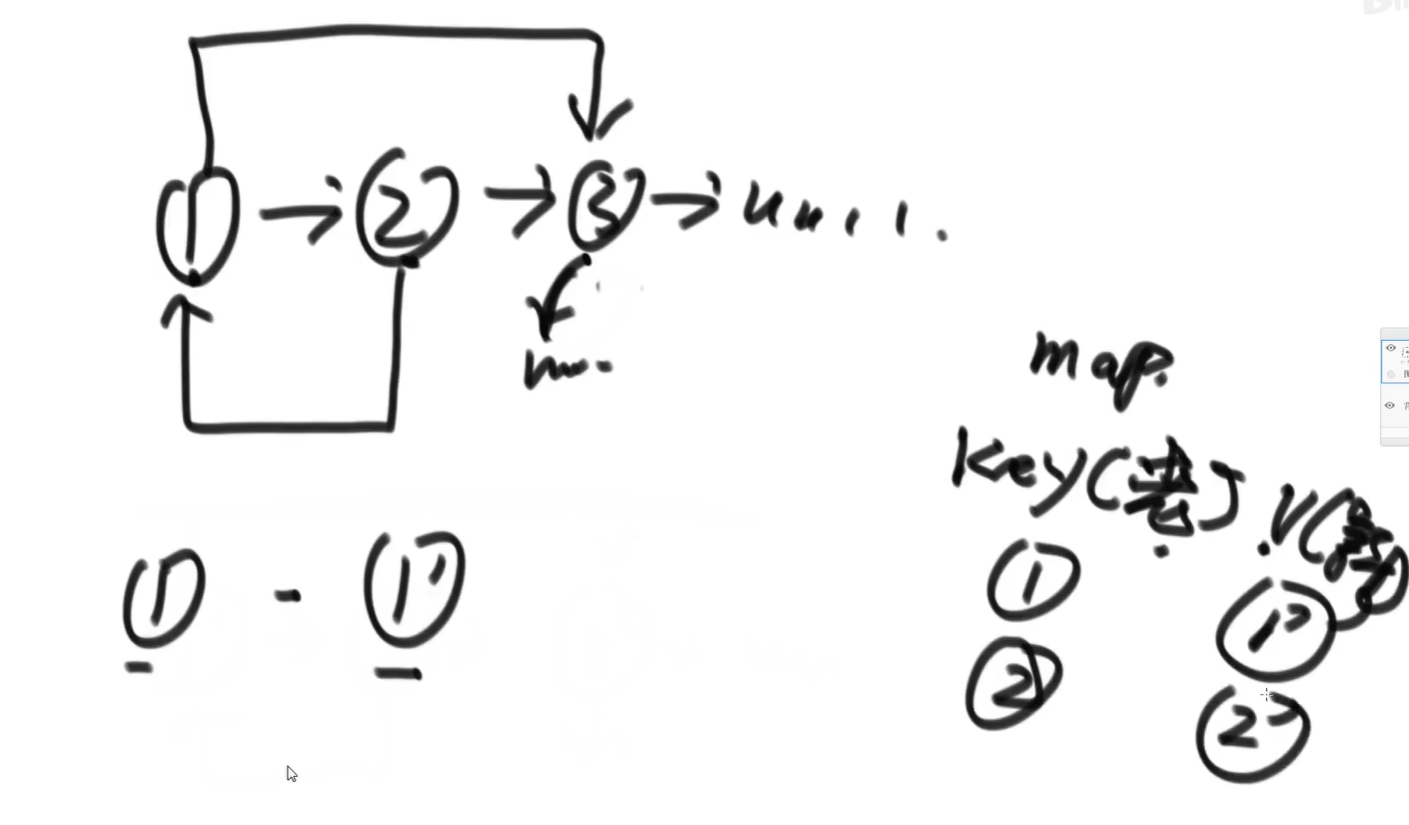
Prepare a hash table, map
key is the Node type, indicating the old Node. value is also the Node type, indicating the cloned new Node corresponding to the old Node
Without considering how to connect the new linked list, copy each old linked list to the new linked list, and then put it in the map,
The second step is to set the pointer in the next and random directions of the new linked list, and traverse the hash table or the old linked list to set the pointer
After traversing 1, the clone node is 1 ', and its next is 2' (because 1next is 2). Similarly, random is set to 3 '. Last return 1 '
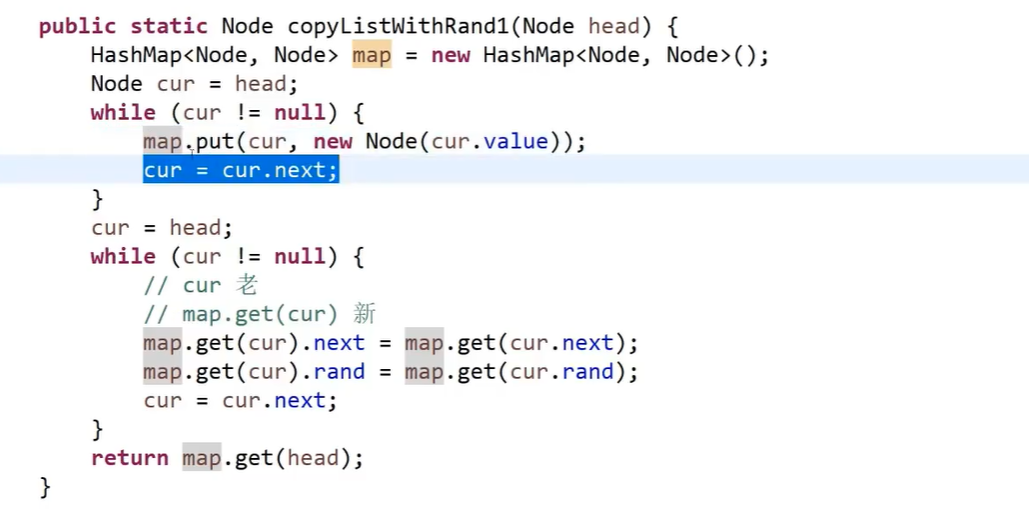
public static Node copyListWithRand1(Node head) {
HashMap<Node, Node> map = new HashMap<Node, Node>();
Node cur = head;
//The first while generates a clone node from the map
while (cur != null) {
map.put(cur, new Node(cur.value));
cur = cur.next;
}
cur = head;
//Traverse the old linked list again
while (cur != null) {
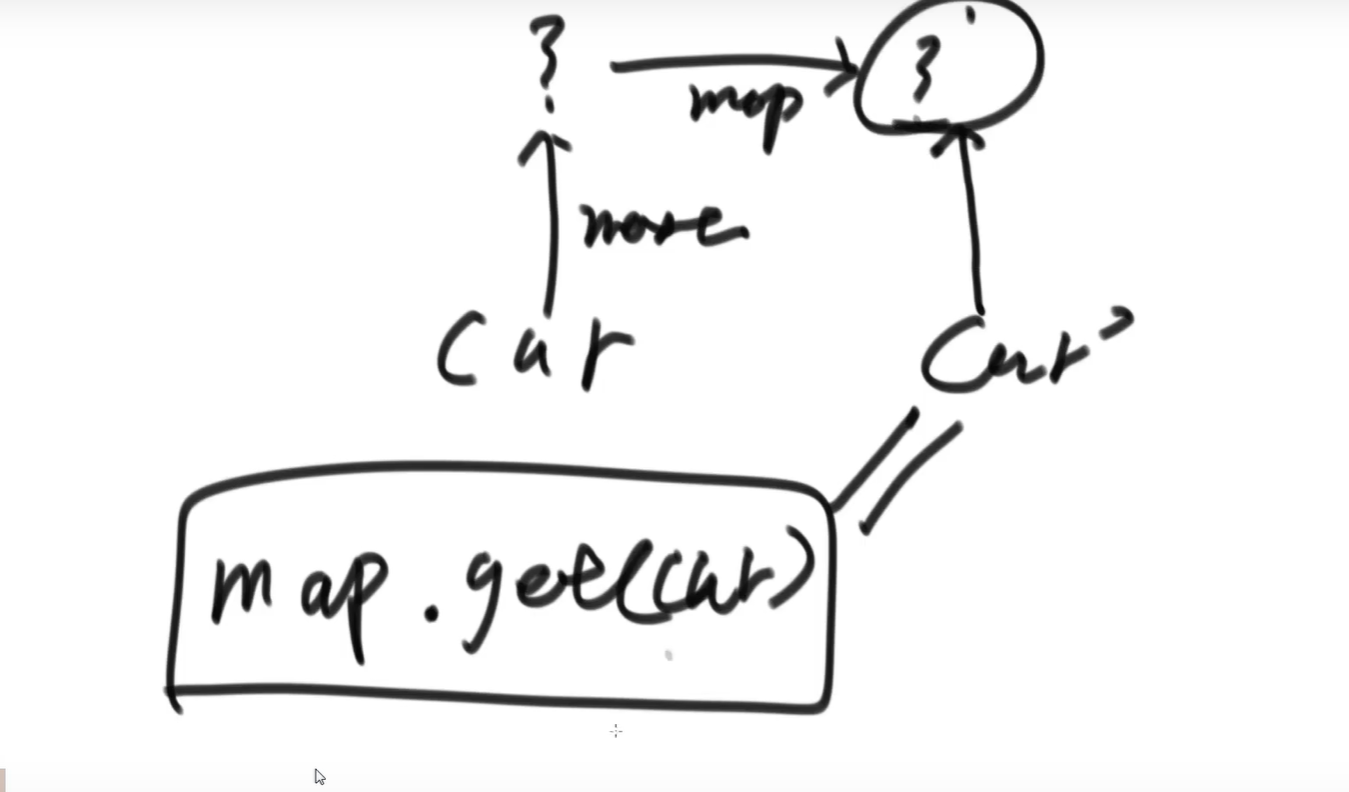
//map.get(cur) = cur ', i.e. clone node
map.get(cur).next = map.get(cur.next);
//Here is the random pointer
map.get(cur).rand = map.get(cur.rand);
cur = cur.next;
}
//The clone node corresponding to the old man is the head of the new head
return map.get(head);
}
Link problem in linked list

Function: a linked list goes down. If there is a ring, it returns the first node into the ring, and if there is no ring, it returns null.
The circle in the figure below is the ring in node
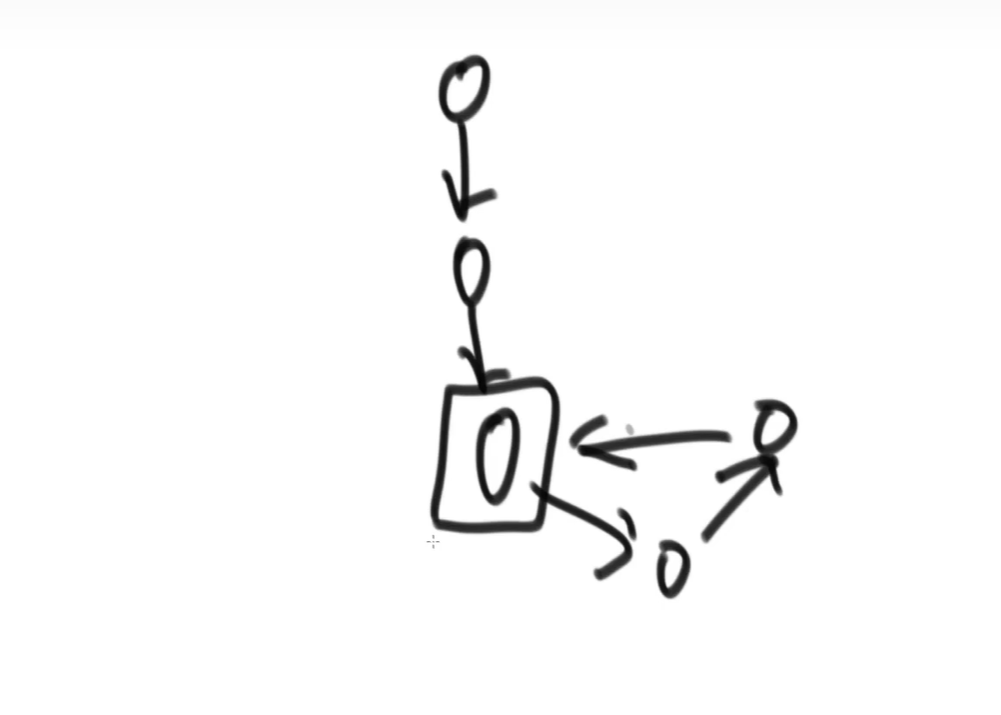
Method 1: use the hash table and set, as shown in the following figure, to traverse the linked list. The first node that appears twice is the ring entry node.
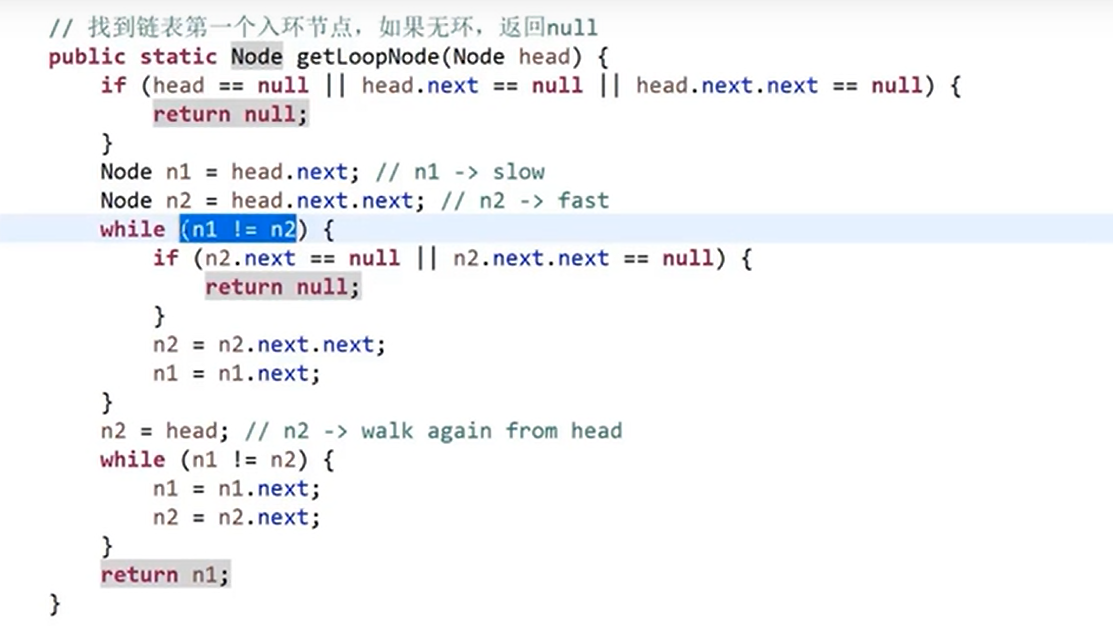
//It is difficult to use fast and slow pointers without additional data structures
PS: if a single linked list has a ring, it will fall into its own ring and can't get out, because there is only one next pointer
The following figure shows the fast and slow pointer. Remember the conclusion: the slow pointer takes one step at a time and the fast pointer takes two steps at a time. If it comes to the end, it means there is no ring.
If the fast and slow pointers meet for the first time at the end (they must meet on the ring), the fast pointer will also take one step at a time and jump to the beginning. If they meet again, they must be at the entrance of the ring.
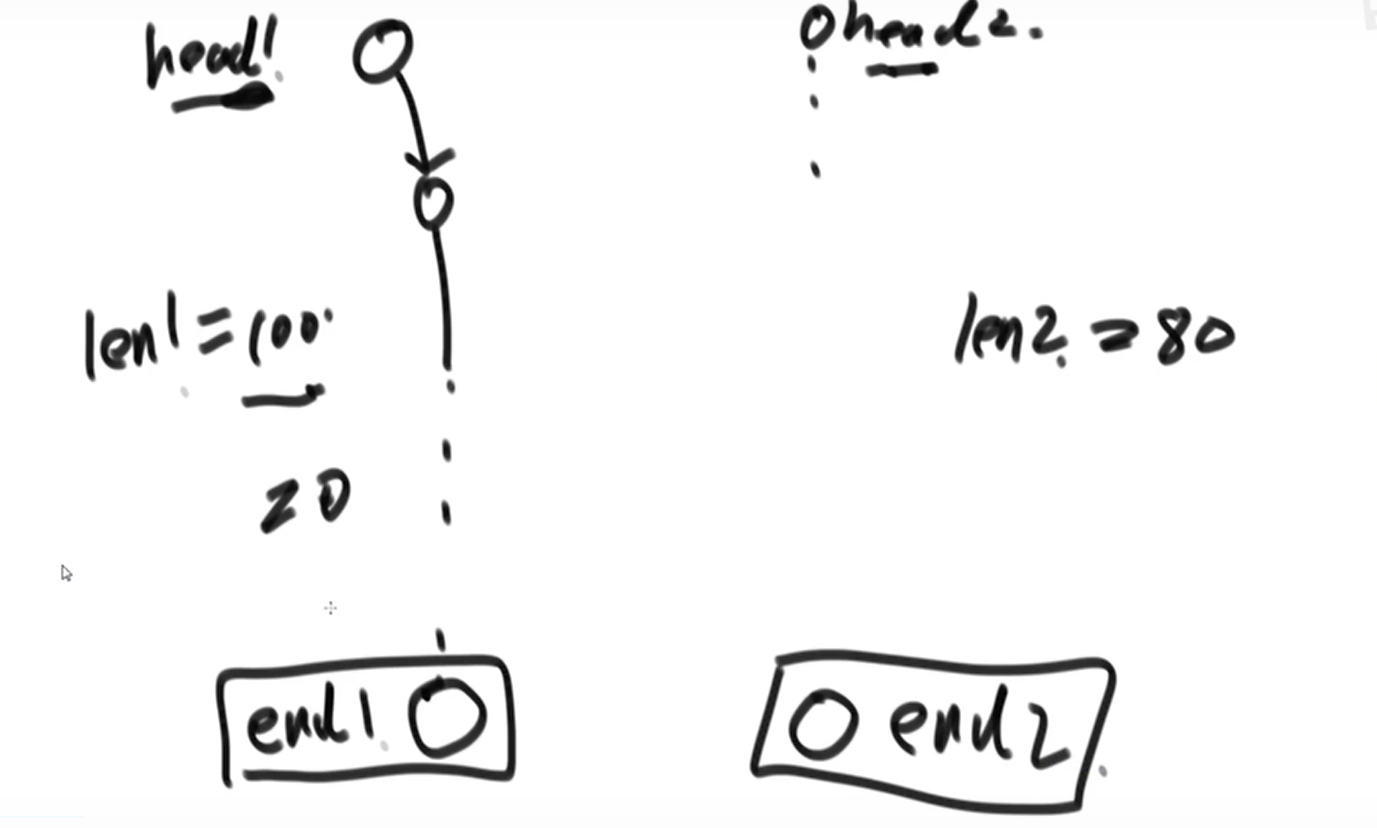
If a node of two linked lists intersects, the subsequent parts of this node are common, as shown in the following figure. According to this conclusion, the following figure compares whether the last node addresses of the two linked lists are equal. If they are not equal, they must not intersect. If equal, start looking for the first intersection node.
For example, the length of linked list 1 is 100 and the length of linked list 2 is 80. First, let linked list 1 take 20 steps, and then linked lists 1 and 2 move forward together. Compare the nodes, and they will surely go to the first common intersection node.

Intersect and disjoint, two cases
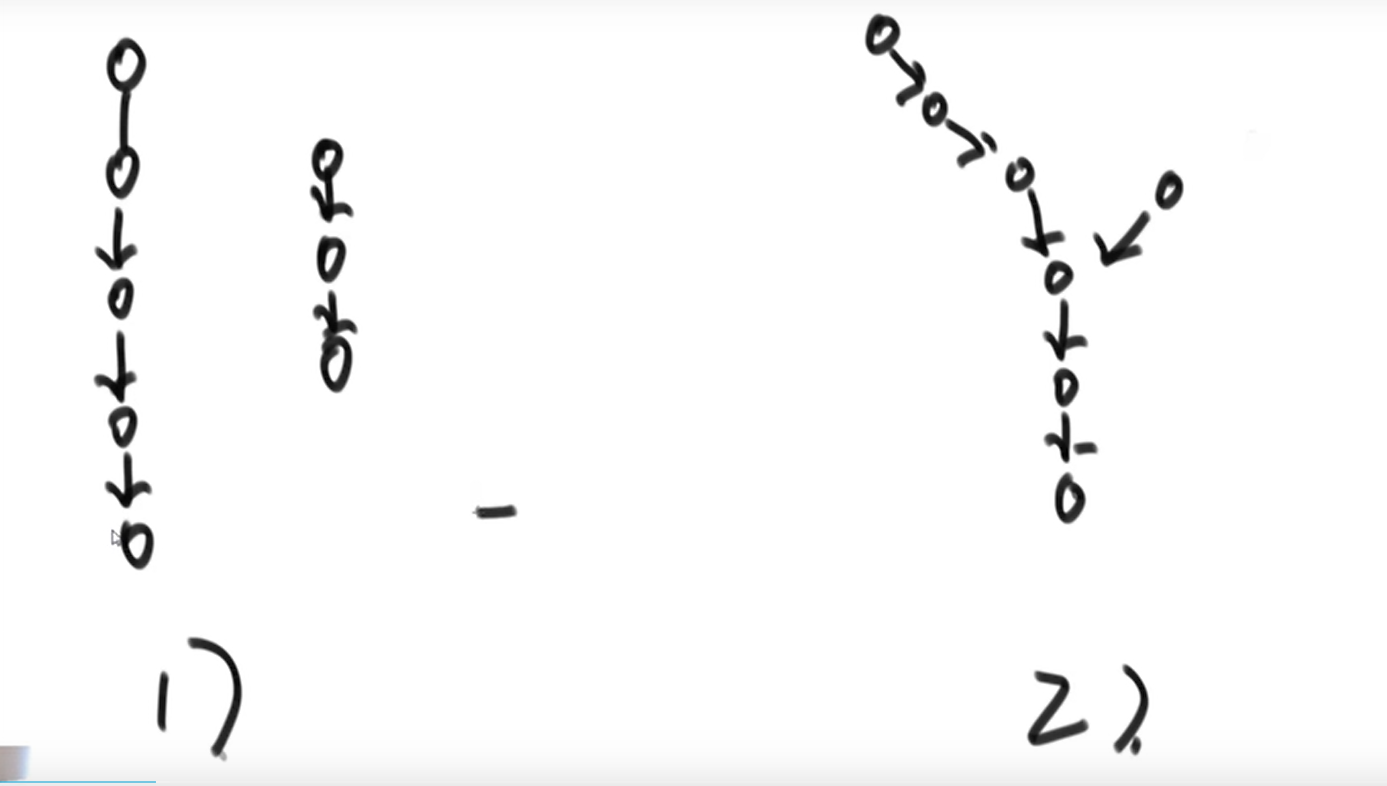
public static Node noLoop(Node head1, Node head2) {
if (head1 == null || head2 == null) {
return null;
}
Node cur1 = head1;
Node cur2 = head2;
int n = 0;
while (cur1.next != null) {
n++;
cur1 = cur1.next;
}
while (cur2.next != null) {
n--;
cur2 = cur2.next;
}
if (cur1 != cur2) {
return null;
}
//n is the length of linked list 1 minus linked list 2,
cur1 = n > 0 ? head1 : head2;//Who grows, whose head becomes curl1
cur2 = cur1 == head1 ? head2 : head1;//Who is short, whose head becomes curl2
n = Math.abs(n);
while (n != 0) {
n--;
cur1 = cur1.next;
}
while (cur1 != cur2) {
cur1 = cur1.next;
cur2 = cur2.next;
}
return cur1;
}
PS: a linked list has rings and a linked list has no rings, so it is impossible to intersect