preface
If violent solutions are used to solve problems, or insert sorting, bubble sorting, etc., and the time complexity is O (n^2), is there a better sorting? Here we will introduce the master formula and merging algorithm in detail, and its time complexity is O(NlogN)
Tip: the following is the main content of this article. The following cases can be used for reference
1, Recursive algorithm
1.1 example code
The solution process of recursive algorithm is to divide the whole problem into several sub problems, then find the sub problems respectively, and finally obtain the solution of the whole problem. This is a divide and conquer idea. Usually, the solution of several subproblems divided by the whole problem is independent, so the solution process corresponds to a recursive tree
Example: find the maximum value on arr[L... R]
Idea: first find the midpoint and divide the array into two regions, arr[L]-arr[mid] and arr[mid+1]-arr[R]
/*
* recursive algorithm
* Example: get a maximum value
* */
public class Recursion {
public static int getMax(int[] arr){
return process(arr,0,arr.length-1);
}
//Find the maximum value on the range of arr[L..R]
public static int process(int[] arr, int L, int R) {
if (L == R){ //When there is only one number, it is returned directly
return arr[L];
}
int mid = L+((R - L) >> 1); //>>: shift one bit to the right, which is equivalent to dividing by 2
int leftMax = process(arr, L, mid); //Left part
int rightMax = process(arr,mid+1,R); //Right part
return Math.max(leftMax,rightMax);
}
public static void main(String[] args) {
int[] arr ={3,2,5,6,7,4};
System.out.println(Recursion.getMax(arr));
}
/*
* master algorithm
* Principle: the range of T(N)=aT(N/b)+O(N^d) subfunctions should be equal
* a:Adjust the sub function several times. b: the scope of the sub function. d: look at the time complexity of other execution
* Judge master recursion
* logb^a<d o(N^d)
* logb^a>d o(N^(logb^a))
* logb^a=d o(N^d*logN)
* */
}
1.2 midpoint overflow
The midpoint of the above code is this line of code
int mid = L+((R - L) >> 1); //Equivalent to int mid = L + (R-L)/2
Why use it like this? Can you write that?
int mid=(L+R)/2;
If the midpoint is calculated in this way, there will be a problem. If the length of the array is relatively large, L+R may overflow
1.3 recursive structure
Suppose the array tested is [3,2,5,6,7,4]
Operation results:
7
Each recursive call to the underlying layer is such a structure diagram
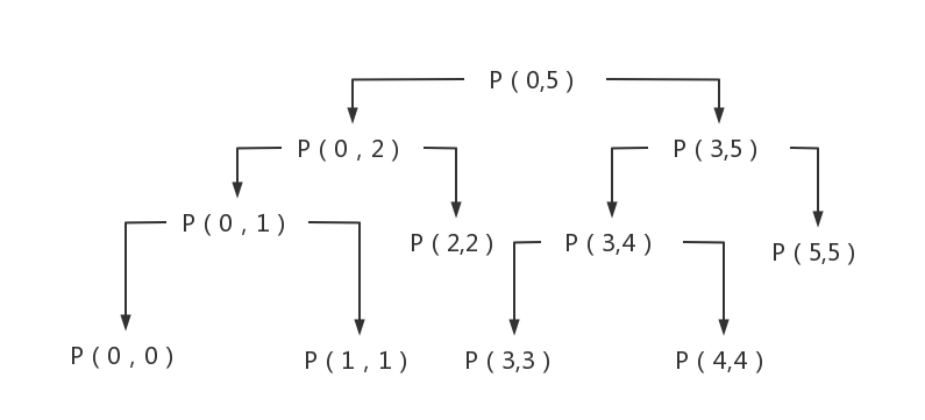
It can be seen from the recursive structure diagram that the final P (0,5) can be obtained only after all the child nodes are summarized. Therefore, the recursive process actually uses the system stack to stack the whole process. Suppose P (0,5) enters the stack, calls P (0,2), enters P (0,2) information into the stack, encounters P (0,1) during execution, and then puts P (0,1) into the stack, and so on. The space of the stack is the height of the whole tree.
This is actually the process of traversing a binary tree.
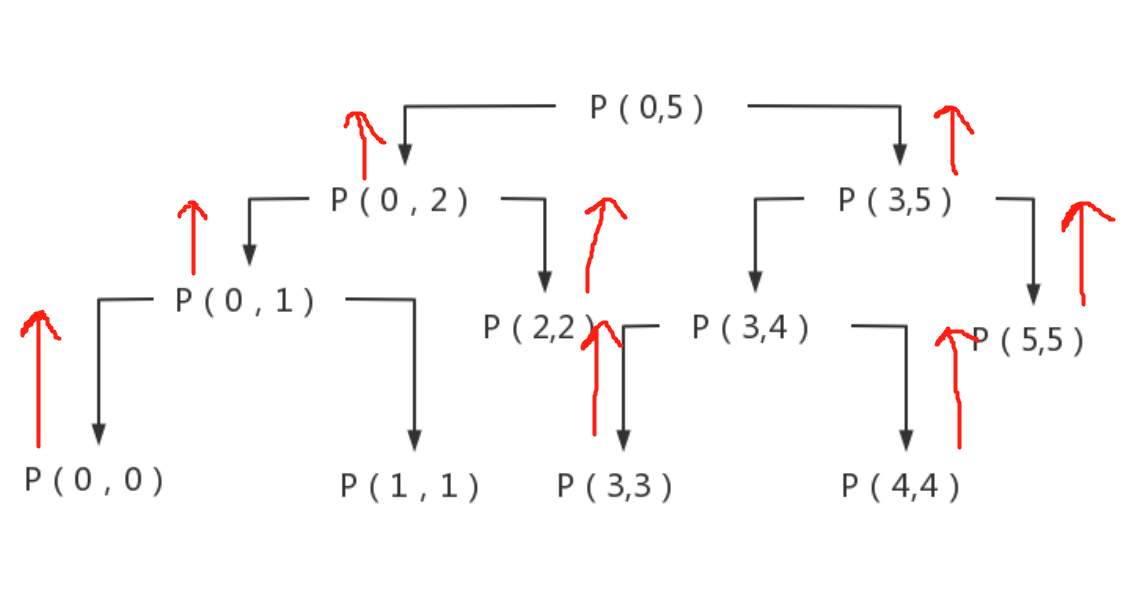
After debugging, it will be found that the recursive results of each layer are returned to the previous layer, so it can be regarded as a process of constantly summarizing from the bottom to the top
2, Master formula
Master formula is a formula used to solve the time complexity of recursive problems.
The formula is as follows:
T[N] = aT[N/b] + O(N^d)
Note: the scope of application is the case where the scale of sub processes is equal, otherwise it is not applicable.
Decomposition view
T[n]: the data scale of the parent problem is N
T[n/b]: the scale of subproblems is N/b
a: Number of times the subproblem was called
O(N^d): the time complexity of the procedure excluding the subproblem call
Using the recursive solution to solve the maximum number above
T[N] = aT[N/b] + O(N^d)
=2T [n / 2] + O(1) < – the last ratio of two numbers, and the time complexity is O(1)
Therefore, the above function satisfies the master formula, and the time complexity can be obtained directly
① When d < log (b) a, the time complexity is O(N^(log(b)a))
② When d=log(b)a, the time complexity is O((N^d)*logN)
③ When d > log (b) a, the time complexity is O(N^d)
Proof process strategy
3, Merge sort
3.1 example code
1) The whole is a simple recursion. The left side is in order, the right side is in order, and the whole is in order
2) The process of making it orderly as a whole uses the exclusive order method
3) master formula is used to solve the time complexity
4) The essence of merging and sorting
Time complexity O(N*logN), additional space complexity O(n)
/*
* Merge (merge) sorting, the whole is a simple recursion, the left side of the order, the right side of the order, so that the whole order
* There is a pointer to the first number on the left and right sides. Each time we compare, the small number is put into the (New) array,
* It's the same size. It's on the left by default. If one side crosses the boundary, just copy the rest
* */
public class MergeSort {
public static void mergeSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
process(arr, 0, arr.length - 1);
}
//recursion
private static void process(int[] arr, int L, int R) {
if (L == R) {
return;
}
int mid = L + ((R - L) >> 1);
process(arr, L, mid);
process(arr, mid + 1, R);
merge(arr, L, mid, R);
}
//Merge
private static void merge(int[] arr, int L, int M, int R) {
int[] help = new int[R - L + 1];
int i = 0;
int p1 = L; //First pointer to the left 1
int p2 = M + 1; //First pointer to the right 2
while (p1 <= M && p2 <= R) { //If pointer 1 and pointer 2 are not out of bounds
//In the new array, the value of the pointer on which side is smaller is placed in turn
help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= M) { //If the p2 pointer (right half) is out of bounds, put all the values in the left half
help[i++] = arr[p1++];
}
while (p2 <= R) { //If the p1 pointer is out of bounds (left half), put all the values in the right half
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) { //The value of the new array
arr[L + i] = help[i];
}
}
}
The merging steps are as follows:
1. In process(arr,L,mid); Keep the left in order
2. In process(arr,mid+1,R); Keep the left in order
3. Get the newly sorted array with the merge method
Many people don't quite understand why the process is already in order. The recursive method is still used here, so the structure diagram is used to explain it
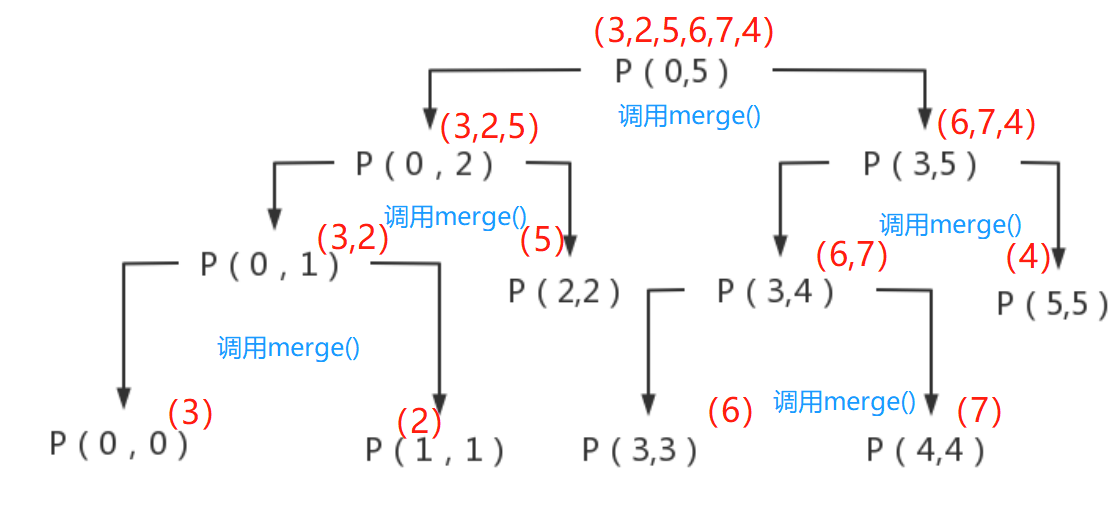
When called, merge() is in process(), so merge() is called every time you recurse, so sorting is actually carried out every time you recursively call merge().
For example, when the first recursive call to merge() occurs, the left part is divided into P(0,0) and P(1,1), that is, the relative left (3) and relative right (2) of the subproblem are merged. Through the algorithm, 2 is put into the new array help [] first, and 3 is put into it again. Therefore, when it is passed to the parent problem of P(0,1), it has been arranged in order - > [2,3] - > and so on. When it is finally summarized to P(0,5), all numbers are in order
3.2 time complexity
Therefore, merging and sorting is a simple recursion. In this problem, it also meets the requirements of master publicity. Its time complexity is:
T(N) = 2T(N/2) + O(N)
a=2 b=2 d=1 ---->d=log(b)a
Therefore, the time complexity is O(N*logN)
3.3 additional space complexity
The additional space complexity of merge sort is O(N)
Because only n extra space is used at most, a space is prepared for each merge and then automatically released (it will be automatically released in java). Therefore, you can apply for a space with a length of N at most. If you reuse it continuously, the additional space complexity is O(N)
3.4 small and problems
Problem Description: in an array, the numbers on the left of each number that are smaller than the current number are accumulated, which is called the small sum of the array. Find the small sum of an array.
Example: [1,3,4,2,5]
1 the number smaller than 1 on the left, no;
3 the number smaller than 3 on the left, 1;
4 numbers smaller than 4 on the left, 1 and 3;
2 the number smaller than 2 on the left, 1;
5 numbers smaller than 5 on the left, 1, 3, 4, 2;
Therefore, the small sum is 1 + 1 + 3 + 1 + 1 + 3 + 4 + 2 = 16
Implement O(N*logN)
Problem solving idea: convert the problem into, how many numbers on the right are larger than this number, then how many should be smaller and
For example:
4 numbers larger than 1 on the right, resulting in 4 small sums of 1;
3. Two numbers larger than 3 on the right produce two small sums;
...
Then use the merging method to compare the left and right sides to obtain the small sum to be generated (see the code for details)
/*
* Small and problems
* In an array, the numbers on the left of each number that are smaller than the current number are added up, which is called the small sum of the array. Find the small sum of an array
* */
class SmallSum {
public static void main(String[] args) {
int[] arr = {1, 3, 4, 2,5};
System.out.println(SmallSum.smallSum(arr));
}
public static int smallSum(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
return process(arr, 0, arr.length - 1);
}
//arr[L,R] not only needs to be arranged in order, but also requires small sum
private static int process(int[] arr, int l, int r) {
if (l == r) {
return 0;
}
int mid = l + ((r - l) >> 1);
return process(arr, l, mid) //The quantity sorted on the left and summed small
+ process(arr, mid + 1, r) //The number of small sums sorted on the right
+ merge(arr, l, mid, r); //The number of small sums generated when the merge is arranged on the left and right
}
public static int merge(int[] arr, int L, int m, int r) {
int[] help = new int[r - L + 1];
int i = 0;
int p1 = L;
int p2 = m + 1;
int res = 0;
while (p1 <= m && p2 <= r) {
//Is the left group smaller than the right group? Yes, multiply the number of all numbers behind the right group (r-p2+1) by the left group, that is, the small sum of this comparison
//You should know that the left and right sides are arranged in order
res += arr[p1] < arr[p2] ? (r - p2 + 1) * arr[p1] : 0;
//If the left group is small, the left pointer moves, otherwise the right pointer moves
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
//The following is a cross-border situation on one side
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[L + i] = help[i];
}
return res;
}
}
Operation results:
16
4, Quick sort 3.0
4.1 example code
package Algorithm;
//Quick sort 3.0
public class QuickSort {
public static void quickSort(int[] arr){
if (arr == null || arr.length < 2){
return;
}
quickSort(arr,0,arr.length -1);
}
//arr[1...r] order
public static void quickSort(int[] arr,int L,int R){
if (L<R){
swap(arr,L+(int)(Math.random()*(R-L+1)),R); //Choose a random position with equal probability and exchange it with the rightmost position
int[] p = partition(arr,L,R); //Returns two values that divide the boundary of the region
quickSort(arr,L,p[0]-1); //< area
quickSort(arr,p[1]+1,R);// >District
}
}
//This is a function that handles arr[1...r]
//By default, it is divided by arr[r], arr[r] - > P < p = = P > P
//Returns an equal and region (left boundary, right boundary), so it returns an array res,res[0] res[1] with a length of 2
private static int[] partition(int[] arr, int L, int R) {
int less = L -1; //< right boundary of area
int more = R; //>Left boundary of area
while (L < more){
if (arr[L] < arr[R]){
swap(arr,++less,L++);
}else if (arr[L] > arr[R]){
swap(arr,--more,L);
}else {
L++;
}
}
swap(arr,more,R);
return new int[]{less+1,more};
}
//The randomly selected number and the rightmost number exchange positions
private static void swap(int[] arr, int random, int R) {
int temp = arr[R];
arr[R] = arr[random];
arr[random] = temp;
}
}
summary
This lesson mainly studies recursive algorithm, merge sort, master formula used to calculate the time complexity of recursive algorithm and quick sort