1. Introduction

Dynamic Time Warping (DTW) has a certain history (proposed by Itakura, a Japanese scholar), and its purpose is relatively simple. It is a method to measure the similarity of two time series with different lengths. It is also widely used, mainly in template matching, for example, in isolated word speech recognition (to identify whether two sounds represent the same word)., gesture recognition, data mining and information retrieval.

1 Overview

Time series is a common representation of data in most disciplines. A common task for time series processing is to compare the similarities of two sequences.
In time series, the length of two time series that need to be comparatively similar may not be equal, and in speech recognition it is shown that different people have different speech speeds. Because voice signals have considerable randomness, even if the same person pronounces the same sound at different times, they cannot have A complete time length. Moreover, the pronunciation speed of different phonemes within the same word is also different.In these complex cases, the distance (or similarity) between two time series cannot be effectively calculated using the traditional Euclidean distance.
2 DTW Method Principle

In time series, the length of two time series that need to be comparatively similar may not be equal, and in speech recognition it is shown that different people have different speech speeds. Also, different phonemes within the same word have different speech speeds, such as someone who drags the "A" sound too long or "i"The hair length is very short. In addition, different time series may only have displacements along the time axis, that is, in the case of restoring displacements, the two time series are identical. In these complex cases, the distance (or similarity) between two time series cannot be effectively calculated using the traditional Euclidean distance.

DTW calculates the similarity between two time series by extending and shortening the time series: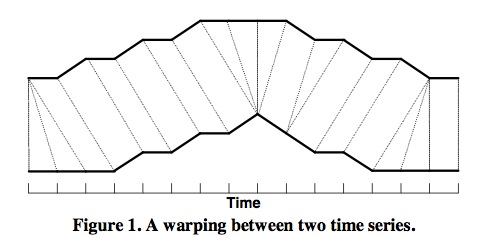

As shown in the figure above, the upper and lower solid lines represent two time series, and the dashed lines between time series represent similar points between two time series. DTW uses the sum of distances between all these similar points, called Warp Path Distance, to measure the similarity between two time series.

2 DTW calculation method:

Make the two time series to calculate similarity X and Y with lengths of |X| and |Y|, respectively.
Routing (Warp Path)
The routed path takes the form W=w1,w2,..., wK, where Max (|X|, |Y|)<=K<=|X|+|Y|.
wk takes the form of (i,j), where I represents the I coordinate in X and j represents the j coordinate in Y.
The rounding path W must start with w1=(1,1) and end with wK=(|X|,|Y|) to ensure that each coordinate in X and Y appears in W.
In addition, the I and j of w(i,j) in W must be monotonically increased to ensure that the dashed lines in Fig. 1 do not intersect. The so-called monotonic increase refers to:


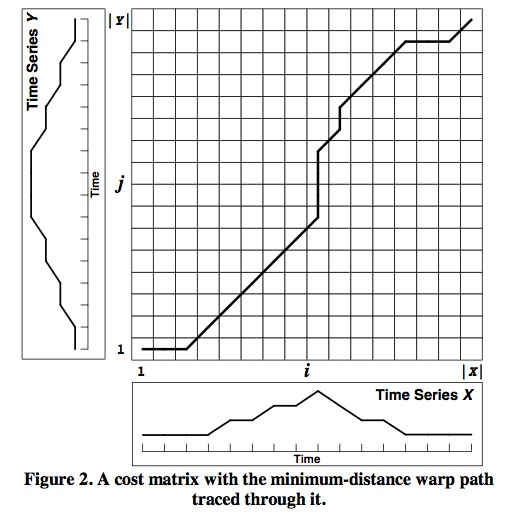
The figure above is Cost Matrix D. D(i,j) represents the integer path distance between two time series of length I and J.

Source Code

clc;
clear;
close all;
waveFile = sprintf('You at the same table.wav');%   Your daughter at the table falls in love with the fairy    Tick    Rainbow
% Read Waveform---Endpoint Detection---Timbre box
    waveFile='You at the same table.wav';
    pivFile = sprintf('You at the same table.piv');
    pivFile=['mfcc' pivFile];
    [y,fs]=audioread(waveFile);  %Read the original file
    figure
    subplot(221)
    plot(y);
    title('Original Graphics');
    
    frame = PointDetect(waveFile);  %Endpoint Detection
    subplot(222)
    plot(frame);
    title('Endpoint Detection');
    
    subplot(223)
    pitch=wave2pitch(frame,fs);   %Calculate pitch
    plot(pitch);
    title('pitch');
function [pitch, pdf, frameEstimated, excitation]=frame2pitch(frame, opt, showPlot)
% frame2acf: PDF (periodicity detection function) of a given frame (primarily for pitch tracking)
%
%	Usage:
%		out=frame2pdf(frame, opt, showPlot);
%			frame: Given frame
%			opt: Options for PDF computation
%				opt.pdf: PDF function to be used
%					'acf' for ACF
%					'amdf' for AMDF
%					'nsdf' for NSDF
%					'acfOverAmdf' for ACF divided by AMDF
%					'hps' for harmonics product sum
%					'ceps' for cepstrum
%				opt.maxShift: no. of shift operations, which is equal to the length of the output vector
%				opt.method: 1 for using the whole frame for shifting
%					2 for using the whole frame for shifting, but normalize the sum by it's overlap area
%					3 for using frame(1:frameSize-maxShift) for shifting
%				opt.siftOrder: order of SIFT (0 for not using SIFT)
%			showPlot: 0 for no plot, 1 for plotting the frame and ACF output
%			out: the returned PDF vector
%
%	Example:
%		waveFile='soo.wav';
%		au=myAudioRead(waveFile);
%		frameSize=256;
%		frameMat=enframe(au.signal, frameSize);
%		frame=frameMat(:, 292);
%		opt=ptOptSet(au.fs, au.nbits, 1);
%		opt.alpha=0;
%		pitch=frame2pitch(frame, opt, 1);
%
%	See also frame2acf, frame2amdf, frame2nsdf.

%	Roger Jang 20020404, 20041013, 20060313

if nargin<1, selfdemo; return; end
if nargin<2||isempty(opt), opt=ptOptSet(8000, 16, 1); end
if nargin<3, showPlot=0; end

%% ====== Preprocessing
%save frame frame
frame=frameZeroMean(frame, opt.zeroMeanPolyOrder);
%frame=frameZeroMean(frame, 0);

frameEstimated=[];
excitation=[];
if opt.siftOrder>0
	[frameEstimated, excitation, coef]=sift(frame, opt.siftOrder);	% Simple inverse filtering tracking
	frame=excitation;
end
frameSize=length(frame);
maxShift=min(frameSize, opt.maxShift);

switch lower(opt.pdf)
	case 'acf'
	%	pdf=frame2acf(frame, maxShift, opt.method);
		pdf=frame2acfMex(frame, maxShift, opt.method);
	%	if opt.method==1
	%		pdfWeight=1+linspace(0, opt.alpha, length(pdf))';
	%		pdf=pdf.*pdfWeight;	% To avoid double pitch error (esp for violin). 20110416
	%	end
	%	if opt.method==2
	%		pdfWeight=1-linspace(0, opt.alpha, length(pdf))';	% alpha is less than 1.
	%		pdf=pdf.*pdfWeight;	% To avoid double pitch error (esp for violin). 20110416
	%	end
		pdfLen=length(pdf);
		pdfWeight=opt.alpha+pdfLen*(1-opt.alpha)./(pdfLen-(0:pdfLen-1)');
		pdf=pdf.*pdfWeight;	% alpha=0==>normalized ACF, alpha=1==>tapering ACF
	case 'amdf'
	%	amdf=frame2amdf(frame, maxShift, opt.method);
		amdf=frame2amdfMex(frame, maxShift, opt.method);
		pdf=max(amdf)*(1-linspace(0,1,length(amdf))')-amdf;
	case 'nsdf'
	%	pdf=frame2nsdf(frame, maxShift, opt.method);
		pdf=frame2nsdfMex(frame, maxShift, opt.method);
	case 'acfoveramdf'
		opt.pdf='acf';
		[acfPitch, acf] =feval(mfilename, frame, opt);
		opt.pdf='amdf';
		[amdfPitch, amdf]=feval(mfilename, frame, opt);
		pdf=0*acf;
		pdf(2:end)=acf(2:end)./amdf(2:end);
	case 'hps'
		[pdf, freq]=frame2hps(frame, opt.fs, opt.zeroPaddedFactor);
	case 'ceps'
		pdf=frame2ceps(frame, opt.fs, opt.zeroPaddedFactor);
	otherwise
		error('Unknown PDF=%s!', opt.pdf);
end

switch lower(opt.pdf)
	case {'acf', 'amdf', 'nsdf', 'amdf4pt', 'acfoveramdf', 'ceps'}
		n1=floor(opt.fs/opt.freqRange(2));		% pdf(1:n1) will not be used
		n2= ceil(opt.fs/opt.freqRange(1));		% pdf(n2:end) will not be used
		if n2>length(pdf), n2=length(pdf); end
		% Update n1 such that pdf(n1)<=pdf(n1+1)
		while n1<n2 & pdf(n1)>pdf(n1+1), n1=n1+1; end
		% Update n2 such that pdf(n2)<=pdf(n2-1)
		while n2>n1 & pdf(n2)>pdf(n2-1), n2=n2-1; end
		pdf2=pdf;
		pdf2(1:n1)=-inf;
		pdf2(n2:end)=-inf;
		[maxValue, maxIndex]=max(pdf2);
		if isinf(maxValue) || maxIndex==n1+1 || maxIndex==n2-1
			pitch=0; maxIndex=nan; maxValue=nan;
		elseif opt.useParabolicFit
			deviation=optimViaParabolicFit(pdf(maxIndex-1:maxIndex+1));
			maxIndex=maxIndex+deviation;
			pitch=freq2pitch(opt.fs/(maxIndex-1));
		else
			pitch=freq2pitch(opt.fs/(maxIndex-1));
		end
	case {'hps'}
		pdf2=pdf;
		pdf2(freq<opt.freqRange(1)|freq>opt.freqRange(2))=-inf;
		[maxValue, maxIndex]=max(pdf2);
	%	if opt.useParabolicFit
	%		deviation=optimViaParabolicFit(pdf(maxIndex-1:maxIndex+1));
	%		maxIndex=maxIndex+deviation;
	%	end
		pitch=freq2pitch(freq(maxIndex));
	otherwise
		error('Unknown PDF=%s!', opt.pdf);
end

if showPlot
	subplot(2,1,1);
	plot(frame, '.-');
	set(gca, 'xlim', [-inf inf]);
	title('Input frame');
	subplot(2,1,2);
	plot(1:length(pdf), pdf, '.-', 1:length(pdf2), pdf2, '.r');
	line(maxIndex, maxValue, 'marker', '^', 'color', 'k');
	set(gca, 'xlim', [-inf inf]);
	title(sprintf('%s vector (opt.method = %d)', opt.pdf, opt.method));
end

% ====== Self demo
function selfdemo
mObj=mFileParse(which(mfilename));
strEval(mObj.example);

3. Operation results