TOPSIS (technology for order preference by similarity to an ideal solution) was first proposed by C.L.Hwang and K.Yoon in 1981. TOPSIS is a method of ranking according to the proximity between a limited number of evaluation objects and idealized objectives. It is to evaluate the relative advantages and disadvantages of existing objects. TOPSIS method is a sort method which approximates to the ideal solution. This method only requires each utility function to be monotonically increasing (or decreasing). TOPSIS method is a commonly used and effective method in multi-objective decision analysis, also known as the good and bad solution distance method.

        The basic process is to unify the original data matrix with the index type (general forward processing) to obtain the forward matrix, then standardize the forward matrix to eliminate the influence of each index dimension, find the optimal scheme and the worst scheme in the limited scheme, and then calculate the distance between each evaluation object and the optimal scheme and the worst scheme respectively, The relative proximity between each evaluation object and the optimal scheme is obtained as the basis for evaluation. This method has no strict restrictions on the data distribution and sample size, and the data calculation is simple and easy.

Step 1: forward the original matrix

Similar to the analytic hierarchy process we mentioned earlier, it needs some indicators to judge.

The four most common indicators:​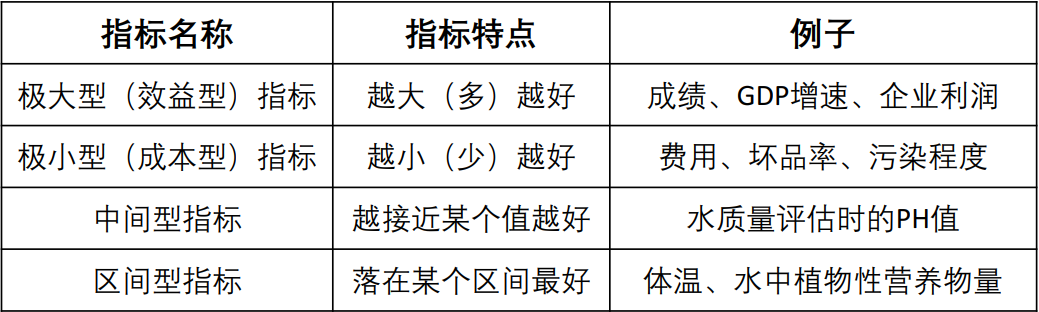

(the so-called forward transformation of the original matrix is to transform all indicator types into very large indicators.)

Formula for converting very small indicators to very large indicators:​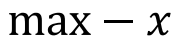

(if all elements are positive, you can also use)

Intermediate indicators:

The index value should not be too large or too small. It is best to take a specific value (such as PH value of water quality assessment)

{a} If it is a group of intermediate index series and the best value is best, the forward formula is as follows: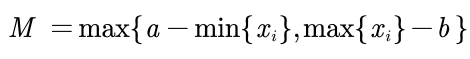

 

 

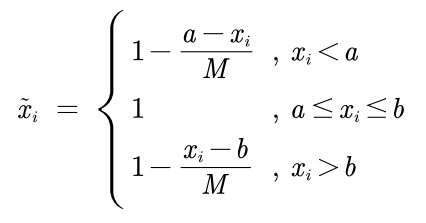
Step 2: standardization of forward matrix (the purpose of standardization is to eliminate the influence of different index dimensions.)

Assuming that there are n objects to be evaluated and m evaluation indexes (which have been normalized), the forward matrix is as follows: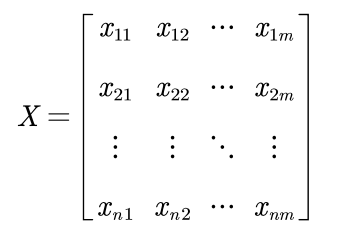

Then, the standardized matrix is recorded as Z, and each element in Z: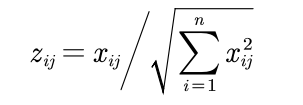

 

It should be noted here that there are many standardization methods, the main purpose of which is to remove the influence of dimension. We may see more standardization methods in the future, for example: (the mean value of x-x) /The standard deviation of X; in most cases, there is no great restriction on which standardized method to choose. Here we use a standardized method used more in previous papers.

Step 3: calculate the score and normalize it

  Suppose there are n objects to be evaluated and the standardized matrix of m evaluation indicators: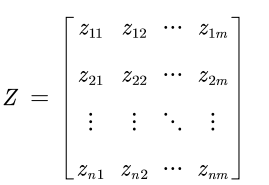

  Define maximum: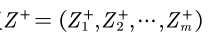

 

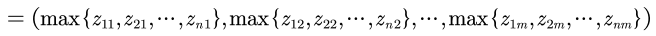
Define minimum value: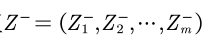 

 

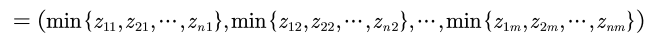
Define the distance between the i(i=1,2,..., n) evaluation object and the maximum value: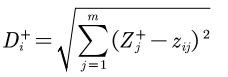

Define the distance between the i(i=1,2,..., n) evaluation object and the minimum value: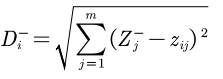 

Then, we can calculate the non normalized score of the i(i=1,2,..., n) evaluation object: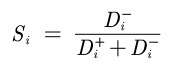

Obviously, 0 ≤ S, ≤ 1, and the larger S, the smaller D +, that is, the closer to the maximum.  

We can normalize the score: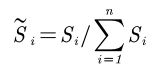, in that case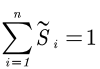(Note: score normalization does not affect sorting)

The code is as follows:

First import your X
clear;clc
load data.mat
 Step 2: determine whether to forward
[n,m] = size(X);
disp(['share' num2str(n) 'Evaluation objects, ' num2str(m) 'Evaluation index'])
Judge = input(['this' num2str(m) 'Whether indicators need to be processed forward, please enter 1 instead of 0:  ']);

if Judge == 1
    Position = input('Please enter the column of the indicator to be processed forward. For example, if columns 2, 3 and 6 need to be processed, you need to enter[2,3,6]:  '); %[2,3,4]
    disp('Please enter the indicator type of these columns to be processed (1: very small, 2: intermediate, 3: interval) ')
    Type = input('For example, if column 2 is very small, column 3 is interval type, and column 6 is intermediate type, enter[1,3,2]:   '); %[2,1,3]
    % be careful, Position and Type Are two row vectors of the same dimension
    for i = 1 : size(Position,2)  %These columns need to be processed separately, so we need to know the total number of times to be processed, that is, the number of cycles
        X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));
    % Positivization It is a function defined by ourselves. Its function is to forward. It receives three parameters in total
    % The first parameter is the column of vectors to forward X(:,Position(i))   Review the knowledge of the previous lecture, X(:,n)Means take the second n All elements of the column
    % The second parameter is the indicator type of the corresponding column (1: very small, 2: intermediate, 3: interval)
    % The third parameter tells the function which column in the original matrix we are dealing with
    % The function has a return value, which returns the index after forward. We can directly assign it to the column vector we originally want to process
    end
    disp('Forward matrix X =  ')
    disp(X)
end

disp('Please enter whether to increase the weight vector. You need to enter 1 instead of 0')
Judge = input('Please enter whether to increase the weight: ');
if Judge == 1
    disp(['If you have three indicators, you need to enter three weights, for example, they are 0.25,0.25,0.5, Then you need to enter[0.25,0.25,0.5]']);
    weigh = input(['You need to enter' num2str(m) 'Weights.' 'Please enter this as a line vector' num2str(m) 'Weights: ']);
    OK = 0;  % It is used to judge whether the user's input format is correct
    while OK == 0
        if abs(sum(weigh) - 1)<0.000001 && size(weigh,1) == 1 && size(weigh,2) == m   % Note that the operation of floating-point numbers is inaccurate.
             OK =1;
        else
            weigh = input('Your input is wrong, please re-enter the weight line vector: ');
        end
    end
else
    weigh = ones(1,m) ./ m ; %If you do not need to add weights, the default weights are the same, that is, they are all 1/m
end

Step 3: standardize the forward matrix
Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);
disp('Standardized matrix Z = ')
disp(Z)

Step 4: calculate the distance from the maximum value and the minimum value, and calculate the score
D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ] .* repmat(weigh,n,1) ,2) .^ 0.5;   % D+ Distance vector from maximum
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ] .* repmat(weigh,n,1) ,2) .^ 0.5;   % D- Distance vector from minimum
S = D_N ./ (D_P+D_N);    % Non normalized score
disp('The final score is:')
stand_S = S / sum(S)
[sorted_S,index] = sort(stand_S ,'descend')

inter2MAX.m
function [posit_x] = Inter2Max(x,a,b)
    r_x = size(x,1);  % row of x
    M = max([a-min(x),max(x)-b]);
    posit_x = zeros(r_x,1);   %zeros Function usage: zeros(3)  zeros(3,1)  ones(3)
    % initialization posit_x The purpose of all 0 initialization is to save processing time
    for i = 1: r_x
        if x(i) < a
           posit_x(i) = 1-(a-x(i))/M;
        elseif x(i) > b
           posit_x(i) = 1-(x(i)-b)/M;
        else
           posit_x(i) = 1;
        end
    end
end

Mid2Max.m
function [posit_x] = Mid2Max(x,best)
    M = max(abs(x-best));
    posit_x = 1 - abs(x-best) / M;
end

Min2Max.m
function [posit_x] = Min2Max(x)
    posit_x = max(x) - x;
     %posit_x = 1 ./ x;    %If x All are greater than 0, which can also be forward
end

% function [Output variable] = Function name((input variable)
% The middle part of the function is the function body
% At the end of the function end ending
% There can be multiple output variables and input variables, separated by commas
% function [a,b,c]=test(d,e,f)
%     a=d+e;
%     b=e+f;
%     c=f+d;
% end
% Custom functions should be placed in a separate m Files cannot be placed directly in the main function (different from most other languages)

Positivization.m
function [posit_x] = Positivization(x,type,i)
% There are three input variables:
% x: The original column vector corresponding to the indicator that needs forward processing
% type:  Type of indicator (1: very small, 2: intermediate, 3: interval)
% i: Which column in the original matrix is being processed
% Output variable posit_x Represents: the forward column vector
    if type == 1  %Very small
        disp(['The first' num2str(i) 'Columns are very small and are being normalized'] )
        posit_x = Min2Max(x);  %call Min2Max Function to forward
        disp(['The first' num2str(i) 'Column miniaturization forward processing completed'] )
        disp('~~~~~~~~~~~~~~~~~~~~Dividing line~~~~~~~~~~~~~~~~~~~~')
    elseif type == 2  %Intermediate type
        disp(['The first' num2str(i) 'Column is intermediate'] )
        best = input('Please enter the best value: ');
        posit_x = Mid2Max(x,best);
        disp(['The first' num2str(i) 'Column intermediate type forward processing completed'] )
        disp('~~~~~~~~~~~~~~~~~~~~Dividing line~~~~~~~~~~~~~~~~~~~~')
    elseif type == 3  %Interval type
        disp(['The first' num2str(i) 'Column is interval type'] )
        a = input('Please enter the lower bound of the interval: ');
        b = input('Please enter the upper bound of the interval: ');
        posit_x = Inter2Max(x,a,b);
        disp(['The first' num2str(i) 'Column interval type forward processing completed'] )
        disp('~~~~~~~~~~~~~~~~~~~~Dividing line~~~~~~~~~~~~~~~~~~~~')
    else
        disp('There is no indicator of this type, please check Type Is there any value in the vector other than 1, 2 and 3')
    end
end