preface

Why did I talk about functions once before and I have to talk about them again now? The first reason is that I said too little before. The second reason is that functions are very important! Very important! Very important! Say something important three times. After all, I started to write a quick start, which is inevitably missing and not detailed enough. Of course, I still post the quick start tutorial here: matlab quick start tutorial

(1) Ordinary function

Note: in MATLAB, functions are defined in separate files. The file name should be the same as the function name.
We create a file named mymax:

function max = mymax(n1, n2, n3, n4, n5)
%This function is to find the maximum value
% Enter five numbers
max =  n1;
if(n2 > max)
    max = n2;
end
if(n3 > max)
   max = n3;
end
if(n4 > max)
    max = n4;
end
if(n5 > max)
    max = n5;
end

We can view our internal description of this function by entering the following command:

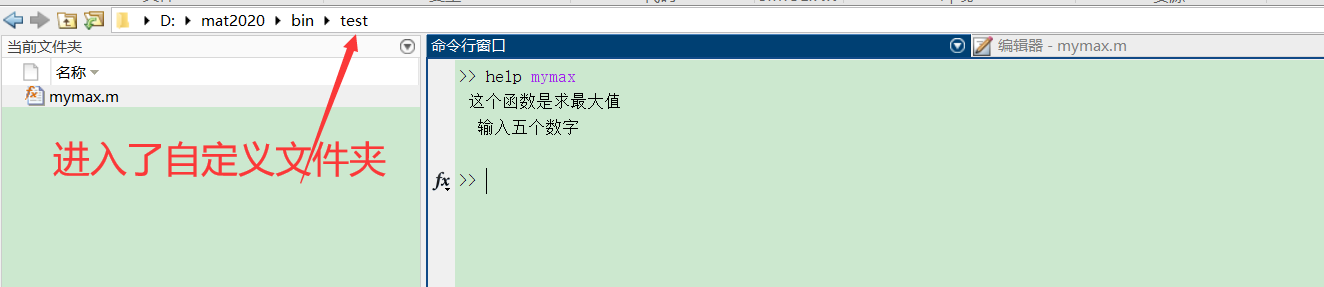
help mymax

Another note: for both large and small projects, create a separate folder and write and execute code in this folder. Otherwise, an error will be reported and the function cannot be found.
For example, I:

Continuing below, calling a function is to pass parameters, because we also define five numbers in the function, and we need to correspond to them one by one. Let me enter five numbers at random:

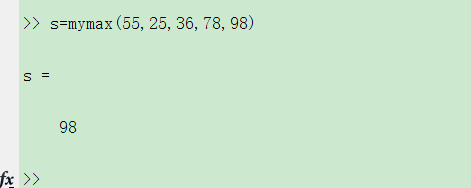
 s=mymax(55,25,36,78,98)

Return result:

(2) Anonymous function

Syntax format:

f = @(arglist)expression

Don't you understand? It doesn't matter. Let's take an example. I created a script named: niming m. So I type niming on the command line to return the result.
The following example is: write an anonymous function power, which will require two numbers as input and return the second number to the power of the first number

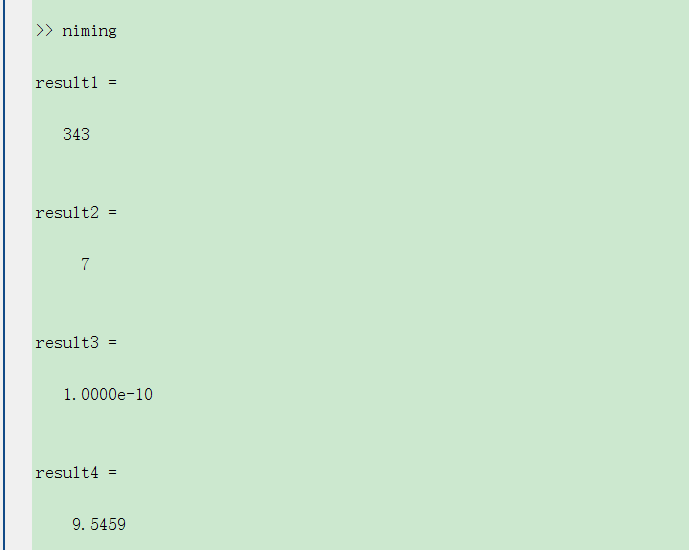
power = @(x, n) x.^n;
result1 = power(7, 3)
result2 = power(49, 0.5)
result3 = power(10, -10)
result4 = power (4.5, 1.5)

Look at the returned results:

(3) Main function and sub function

Take an example to understand, as follows:
We write a quadratic function to calculate the root of a quadratic equation of one variable. The function will require three inputs, quadratic coefficients, linear cooperation, efficient and constant terms, and it will return the root. Function file rectangular M will include the main quadratic function and sub function disc to calculate the discrimination.
code:

function [x1,x2] = quadratic(a,b,c)
% It takes 3 input arguments
d = disc(a,b,c); 
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end % end of quadratic

function dis = disc(a,b,c) 
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end % end of sub-function

It's a solution to a quadratic equation in one variable. There's no need to say too much. Is to transfer the following disc function to the above d. The main function and the sub function are related. So I enter in the command line window:

s=quadratic(1,2,3)

Return as follows:

(4) Nested function

The syntax format is:

function x = A(p1, p2)
...
B(p2)
   function y = B(p3)
   ...
   end
...
end

For example, the application of nested functions in solving the upper bound of integrals

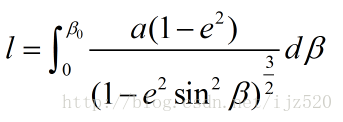
code:

function sol=example1(a,e,l)
    function f=fun1(beta)
        f=a.*(1-e.^2)./(1-e.^2*sin(beta).^2).^(3/2);
    end
    function g=fun2(beta0)
        g=quadl(@fun1,0,beta0)-l;
    end
sol=fzero(@fun2,3);
end

Enter an example as follows:

s=example1(20,0.6,6)

return:

(5) Private function

A private function is a main function, which can only see a limited set of other functions. If you do not want to publicly execute a function, you can create a private function. Private functions reside in a subfolder with a special name. They are visible only in the parent folder function.
Let's take solving a quadratic equation of one variable as an example:
Create a file named disc M file:

function dis = disc(a,b,c) 
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end % end of sub-function

And then create the quadric3 M file:

function [x1,x2] = quadratic3(a,b,c)
% It takes 3 input arguments
d = disc(a,b,c); 
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end % end of quadratic3

So I enter on the command line:

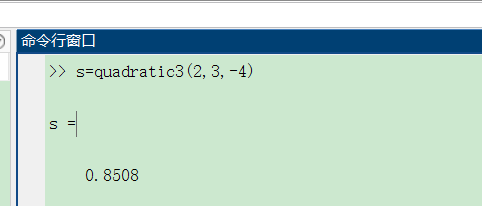
s=quadratic3(2,3,-4)

return:

(6) Global variable

The so-called global variable means that global variables can be shared by more than one function. For this, you need to declare variables as global, which can be used in all functions. That is, use TLTAL to make it public.

The new file name is: average M code is as follows

function avg = average(nums)
global TOTAL
avg = sum(nums)/TOTAL;
end

Run after command line or script input:

global TOTAL;
TOTAL = 10;
n = [34, 45, 25, 45, 33, 19, 40, 34, 38, 42];
av = average(n)

return:

Of course, it is convenient for lazy people to operate. I still put the code file in github and download it myself.

https://github.com/89461561511656/matlab