1, Introduction to orthogonal Latin square scrambling and two-dimensional Arnold scrambling
0 Introduction
With the rapid development of communication technology, more and more fields need to transmit digital image signals, so the security of information transmission is becoming more and more important. There are two protection technologies commonly used in digital image communication: digital watermarking technology and image encryption technology. The former protection technology is not suitable for the transmission of confidential images because it does not change the visibility of images. The latter technology changes the visibility of the image through encryption operation, so that the original image becomes indistinguishable, and the original image can only be obtained through the corresponding decryption algorithm. With the development of communication technology, image encryption technology has been more and more widely used because of its good confidentiality.
A random sequence generator is needed in the encryption algorithm. Because the discrete chaotic system is easy to implement, and the chaotic system is extremely sensitive to parameters and initial conditions, taking it as the key, the system has excellent cryptographic characteristics. At the same time, its irregularity in the two-dimensional phase plane makes it more suitable for image encryption.
According to the storage characteristics of image data, an image encryption algorithm is designed by using discrete chaotic dynamic system. All keys are generated by discrete chaotic mapping, so the algorithm does not affect the efficiency and speed of encryption / decryption due to the increase of key setting. Due to the use of chaotic mapping, it increases the difficulty of decoding and improves the security. The simulation results show that the algorithm can effectively encrypt / decrypt the number of digital images.
1 Orthogonal Latin square scrambling
1.1 basic concepts
Definition 1 consists of elements 1, 2, 3,..., n to form an n × Square matrix of n (aij) n × n. Such a square matrix is called an n-order Latin square.
Definition 2 let A = (aij) n × n, B= (bij) n × N is two n × Latin square of N, if square matrix ((aij, bij)) n × If n2 even pairs (aij, bij) in n are different from each other, i, j=1, 2,..., N, then A and B are called mutually orthogonal Latin squares, or A and B are called n-order orthogonal Latin squares.
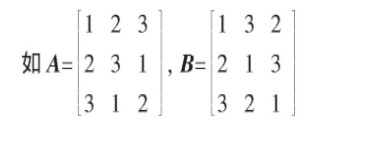
Then it consists of A and B 3 × Even pair square matrix of 3

There are no same elements, so A and B are third-order orthogonal Latin squares.
1.2 related theorems
Theorem 1 the number of n-order Latin squares orthogonal to each other does not exceed n-1, that is, if A1, A2,..., Ak are n-order Latin squares orthogonal to each other, then k ≤ n-1.
Theorem 2 let n ≥ 3 and n=p α, p is a prime, α Is a positive integer, then there are n-1 orthogonal Latin squares of order n A1, A2,..., An-1, and let
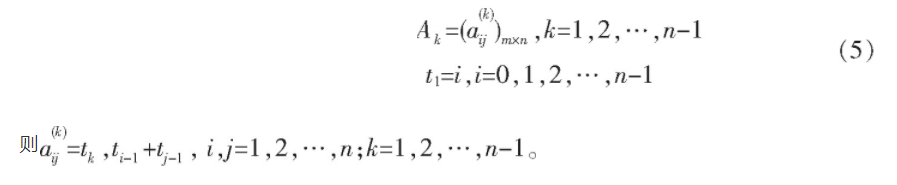
Theorem 3 if A1, A2,..., Am are pairwise orthogonal Latin square groups, and let
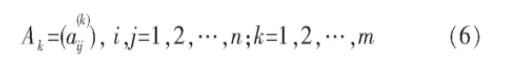
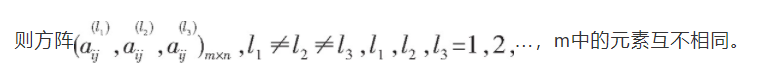
1.3 digital image scrambling based on orthogonal Latin square
Image scrambling originated from some cryptographic algorithms used in the early stage of cryptography. Its function is to rearrange the position of pixels in the image and transform the original image into a disordered new image. To restore the original image, it must ensure that the transformation between the original image and the transformed image is 1-1 mapping (bijection), and the orthogonal Latin square has this property. The specific methods are:

According to Theorem 3, for images in three-dimensional space, the purpose of digital image scrambling can also be achieved by using orthogonal Latin squares. Because the orthogonal Latin square group contains n-1 mutually orthogonal Latin squares, there are n (n-1) kinds of image scrambling methods. For three-dimensional images, there are n (n-1) (n-2).
1.4 new image encryption algorithm
The main idea of the algorithm proposed in this paper is: according to the Logistic map, using the key x0, μ Generate chaotic sequence xk, generate gray scrambling matrix G * from xk, encrypt the original image with matrix G *, and then apply scrambling based on orthogonal Latin square to complete the double encryption of the image. The complete scrambling and restoration algorithm is shown in Figure 1.
The algorithm uses XOR operation to change the pixel value because XOR operation is mathematically reversible and can realize the inverse operation of the algorithm. The steps are as follows:
(1) According to the Logistic mapping, the key is used μ, x0. Generate a set of chaotic sequences xk, and take m from XR (r > 0) × N elements constitute M × Matrix B, B (i, j) ∈ [0, 1] of n. Transform B (i, j) according to equation (7) to generate encryption matrix C, C (i, j) ∈ [0, 255].
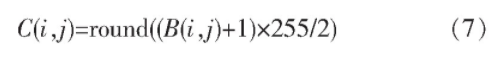
(2) The original image matrix is A, and the pixel value (i, j) of each pixel in A is XOR with C (i, j) to obtain the primary encrypted image M.
(3) The image M is subjected to orthogonal Latin square scrambling transformation to obtain the final encrypted image I *. The decryption process is just the reverse process of encryption hiding.
(4) The image I * is transformed by inverse orthogonal Latin square to obtain the image M.
(5) According to the one-dimensional Logistic function, parameters and initial values, the one-dimensional random sequence is obtained to form the encryption matrix C.
(6) The encryption matrix C performs XOR operation with the image M to obtain the original image matrix A.

Figure 1 encryption algorithm model
2 Arnold scrambling
2.1 Arnold transform
The point (x, y) on the N*N image is transformed into (x ', y') by the following transformation, as shown in formula (1), which is called Arnold transformation Through the transformation formula, it can be found that the essence of the transformation is the transformation of the position of the points, and this transformation ensures that the points before and after the transformation maintain a one-to-one correspondence.
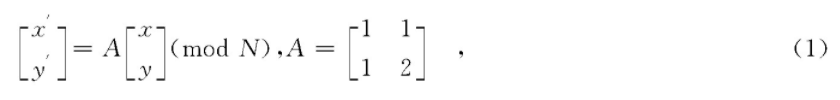
If the output of one transformation is used as the input of the next transformation, it is an iterative transformation, as shown in equation (2) When the scrambling effect of one transform is poor, iterative transform is often needed to obtain better scrambling effect.
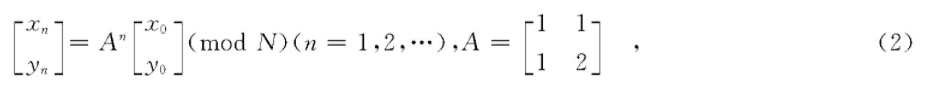
2.2 image encryption and decryption based on Arnold transform
Image encryption, also known as image scrambling, is the confusion and diffusion of image pixels, so that the encrypted image can not obtain effective information visually Spatial encryption is a common method, which is divided into spatial scrambling and sequence encryption Spatial scrambling is to transform the pixel coordinates to make them chaotic, and restore the original pixel coordinates during decryption Image encryption can be used not only as an independent information hiding method, but also as the preprocessing of image watermark in digital watermarking technology.
The encrypted image can be a gray image or a color image. If it is a gray image, the gray value of each point needs to be brought to the new coordinate point. If it is a color image, the RGB value of each point needs to be brought to the new coordinate point The image encrypted in this paper is a color image. Therefore, firstly, the RGB value at the original point (x, y) is saved, then the position of the point (x, y) is changed to (x ', y') by Arnold transform, and the RGB value at the original point (x, y) is brought to (x ', y') We use 256 * 256 color image as the original image, as shown in Figure 1a. We use equation (1) to perform Arnold transformation on the original image under the platform of Visual Studio 2008, and the transformed effect is shown in Figure 1b
It can be seen from Figure 1 that more information will still be left after one Arnold transformation of the image. Therefore, Arnold transformation continues to be used on this basis. After five transformations (see Figure 2b), it is difficult to obtain any valuable information visually, which plays the role of image encryption visually At the same time, the number of transformations can often be used as the key, so as to improve the security to a certain extent.

Fig. 1 original diagram and results of one-time Arnold transformation

Fig. 2 results of the 2nd and 5th Arnold transform
However, the encryption at this time is not completely reliable. If Arnold transformation is known as the encryption method, the original image can be decrypted after several transformations by the violent solution method Therefore, in general, we often need to add keys (ku, kv) to Arnold transform to improve security. The formula is as follows:
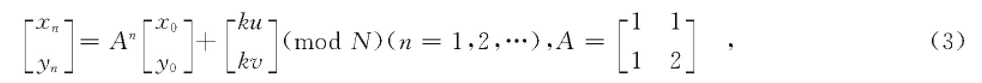
When the image needs to be decrypted, it is decrypted according to the one-to-one correspondence between the pixel points in the encrypted image and the pixel points in the original image. Therefore, the process of image decryption is: calculate the coordinates (x ', y') of the pixel points in the new image according to Arnold transformation according to the coordinates (x, y) of the pixel points in the original image, obtain the RGB value of the new pixel points (x ', y') and return the value to (x, y) According to the transformation times used in the encryption process, when decrypting, repeat the above process for the corresponding times to restore the original image (see Figure 3).
2.3 image encryption based on 3D Arnold transform
The image scrambling mentioned above achieves the goal by disturbing the pixel position, and the color component value of the image remains unchanged Therefore, in order to improve the encryption effect, we can encrypt the image by changing the value of RGB color component on the premise that the pixel position is disordered The following three-dimensional Arnold transform (such as equation 4) is used to change the RGB component value.

We take the Arnold transformed image as the original image, and on this basis, we use the above formula to disturb the RGB of each pixel, and obtain the results as shown in Fig. 4 Through the combination of the two encryption methods, the security of the encrypted image is further improved The value in equation 4 can be changed accordingly, and the number of transformations can be used as a key to improve security.

Fig. 3 the result of the fifth Arnold transform and the restored encrypted image

Fig. 4 encrypted image after RGB scrambling as a result of the first Arnold transform
2, Partial source code
function varargout = ladingfang(varargin)
% LADINGFANG M-file for ladingfang.fig
% LADINGFANG, by itself, creates a new LADINGFANG or raises the existing
% singleton*.
%
% H = LADINGFANG returns the handle to a new LADINGFANG or the handle to
% the existing singleton*.
%
% LADINGFANG('CALLBACK',hObject,eventData,handles,...) calls the local
% function named CALLBACK in LADINGFANG.M with the given input arguments.
%
% LADINGFANG('Property','Value',...) creates a new LADINGFANG or raises the
% existing singleton*. Starting from the left, property value pairs are
% applied to the GUI before ladingfang_OpeningFunction gets called. An
% unrecognized property name or invalid value makes property application
% stop. All inputs are passed to ladingfang_OpeningFcn via varargin.
%
% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one
% instance to run (singleton)".
%
% See also: GUIDE, GUIDATA, GUIHANDLES
% Edit the above text to modify the response to help ladingfang
% Last Modified by GUIDE v2.5 05-Jan-2005 22:18:40
% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name', mfilename, ...
'gui_Singleton', gui_Singleton, ...
'gui_OpeningFcn', @ladingfang_OpeningFcn, ...
'gui_OutputFcn', @ladingfang_OutputFcn, ...
'gui_LayoutFcn', [] , ...
'gui_Callback', []);
if nargin & isstr(varargin{1})
gui_State.gui_Callback = str2func(varargin{1});
end
if nargout
[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
gui_mainfcn(gui_State, varargin{:});
end
% End initialization code - DO NOT EDIT
% --- Executes just before ladingfang is made visible.
function ladingfang_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% varargin command line arguments to ladingfang (see VARARGIN)
% Choose default command line output for ladingfang
handles.output = hObject;
% Update handles structure
guidata(hObject, handles);
% This sets up the initial plot - only do when we are invisible
% so window can get raised using ladingfang.
if strcmp(get(hObject,'Visible'),'off')
% plot(rand(5));
end
global h1 h2
h1=handles.axes1;
h2=handles.axes2;
%-----------------Initialize interface properties
set(handles.edit1,'string','1');
set(handles.edit2,'string','2');
set(handles.edit3,'string','125');
set(handles.pushbutton2,'Visible','off');
G=imread('LENA256.BMP');
set(gcf,'CurrentAxes',h1);
imshow(G);
title('Original image');
set(h2,'Visible','off');
% UIWAIT makes ladingfang wait for user response (see UIRESUME)
% uiwait(handles.figure1);
% --- Outputs from this function are returned to the command line.
function varargout = ladingfang_OutputFcn(hObject, eventdata, handles)
% varargout cell array for returning output args (see VARARGOUT);
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% Get default command line output from handles structure
varargout{1} = handles.output;
%%%%%%%%%%%%%%%%%%%%%%%%%%%% Encryption function %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function pushbutton1_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton1 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
axes(handles.axes1);
cla;
global h1 h2
%------------Update and obtain the properties of each object
Times = str2num(get(handles.edit1, 'string'));
X= str2num(get(handles.edit2, 'string'));
Y= str2num(get(handles.edit3, 'string'));
popup_sel_index = get(handles.popupmenu1, 'Value');
switch popup_sel_index
case 1
G=imread('lena256.bmp');
set(gcf,'CurrentAxes',h1);
imshow(G);
title('Original image');
%-----Verify the validity of the input data
N = str2double(get(handles.edit1,'String'));
Errstr = '';
Errstr = 'The number of transformations must be a positive integer!';
end
if ~isempty(Errstr)
errordlg(Errstr);
return
end
D(1) =str2double(get(handles.edit2,'String'));
D(2) =str2double(get(handles.edit3,'String'));
Errstr = '';
if isnan(D(1)) | ~(floor(D(1)) == D(1)) | (D(1) < 1)| (D(1)>255)
Errstr = 'Parameter 1 must be a positive integer from 1 to 255!';
end
if ~isempty(Errstr)
errordlg(Errstr);
return
end
Errstr = '';
if isnan(D(2)) | ~(floor(D(2)) == D(2)) | (D(2) < 1)| (D(1)>255)
Errstr = 'Parameter 2 must be a positive integer from 1 to 255!';
end
if ~isempty(Errstr)
errordlg(Errstr);
return
end
if D(1) == D(2)
Errstr = 'Parameter 1 and parameter 2 must be different!';
end
if ~isempty(Errstr)
errordlg(Errstr);
return
end
%-----------End of verification
%-----------Some controls are disabled during calculation
mousefrm(0,'watch');
set(handles.popupmenu1,'enable','off');
set(handles.popupmenu2,'enable','off');
set(handles.edit1,'enable','off');
set(handles.edit2,'enable','off');
set(handles.edit3,'enable','off');
set(handles.pushbutton1,'enable','off');
set(handles.pushbutton2,'enable','off');
%----------------------------------------
set(gcf,'CurrentAxes',h2);
I=G;
[u,v]=zhengjiaodui(X,Y);
%----------Restore control availability
set(handles.popupmenu1,'enable','on');
set(handles.popupmenu2,'enable','on');
set(handles.edit1,'enable','on');
set(handles.edit2,'enable','on');
set(handles.edit3,'enable','on');
set(handles.pushbutton1,'enable','on');
set(handles.pushbutton2,'enable','on');
mousefrm(0,'arrow');
%--------------------------------------
case 2
G=imread('LENA256.BMP');
set(gcf,'CurrentAxes',h1);
imshow(G);
title('Original image');
%-----Verify the validity of the input data
N = str2double(get(handles.edit1,'String'));
Errstr = '';
if isnan(N) | ~(floor(N) == N) | (N <= 0)
Errstr = 'The number of transformations must be a positive integer!';
end
if ~isempty(Errstr)
errordlg(Errstr);
return
end
D(1) =str2double(get(handles.edit2,'String'));
D(2) =str2double(get(handles.edit3,'String'));
Errstr = '';
if isnan(D(1)) | ~(floor(D(1)) == D(1))
Errstr = 'Parameter 1 must be an integer!';
end
if ~isempty(Errstr)
errordlg(Errstr);
return
end
Errstr = '';
if isnan(D(2)) | ~(floor(D(2)) == D(2))
Errstr = 'Parameter 2 must be an integer!';
end
if ~isempty(Errstr)
errordlg(Errstr);
return
end
%-----------End of verification
mousefrm(0,'watch');
set(gcf,'CurrentAxes',h2);
positiontrans(G,Times,X,Y);
title('After encryption');
mousefrm(0,'arrow');
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%% Decryption function %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function pushbutton2_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton2 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
axes(handles.axes1);
cla;
global h1 h2
Times = str2num(get(handles.edit1, 'string'));
X= str2num(get(handles.edit2, 'string'));
Y= str2num(get(handles.edit3, 'string'));
Times = str2num(get(handles.edit1, 'string'));
UNCODE=imread('code.bmp');
set(gcf,'CurrentAxes',h1);
imshow(UNCODE);
title('Before decryption');
%-----Verify the validity of the input data
N = str2double(get(handles.edit1,'String'));
Errstr = '';
if isnan(N) | ~(floor(N) == N) | (N <= 0)
Errstr = 'The number of transformations must be a positive integer!';
end
if ~isempty(Errstr)
errordlg(Errstr);
return
end
D(1) =str2double(get(handles.edit2,'String'));
D(2) =str2double(get(handles.edit3,'String'));
Errstr = '';
if isnan(D(1)) | ~(floor(D(1)) == D(1)) | (D(1) < 1)| (D(1)>255)
Errstr = 'Parameter 1 must be a positive integer from 1 to 255!';
end
if ~isempty(Errstr)
errordlg(Errstr);
return
end
Errstr = '';
if isnan(D(2)) | ~(floor(D(2)) == D(2)) | (D(2) < 1)| (D(1)>255)
Errstr = 'Parameter 2 must be a positive integer from 1 to 255!';
end
if ~isempty(Errstr)
errordlg(Errstr);
return
end
if D(1) == D(2)
Errstr = 'Parameter 1 and parameter 2 must be different!';
end
if ~isempty(Errstr)
errordlg(Errstr);
return
end
3, Operation results
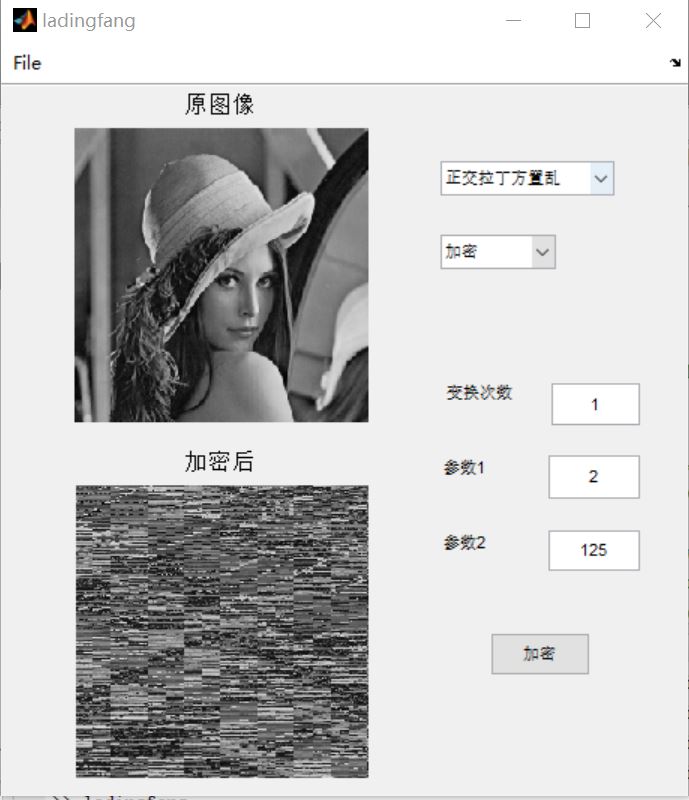
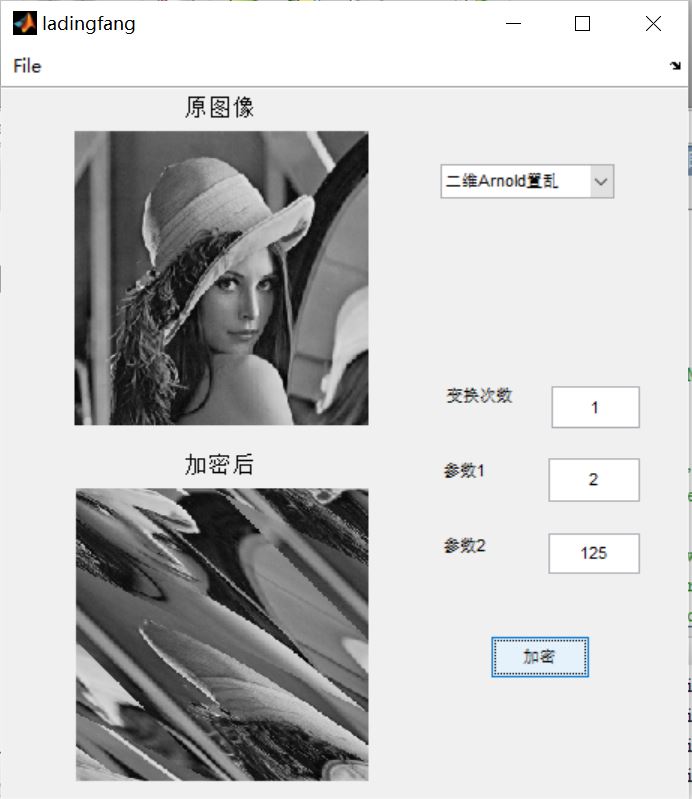
4, matlab version and references
1 matlab version
2014a
2 references
[1] Cai Limei MATLAB image processing -- theory, algorithm and example analysis [M] Tsinghua University Press, 2020
[2] Yang Dan, Zhao Haibin, long Zhe Detailed explanation of MATLAB image processing example [M] Tsinghua University Press, 2013
[3] Zhou pin MATLAB image processing and graphical user interface design [M] Tsinghua University Press, 2013
[4] Liu Chenglong Proficient in MATLAB image processing [M] Tsinghua University Press, 2015