1, Flower pollination algorithm

Flower Pollination Algorithm (FPA) was proposed by Yang, a scholar at Cambridge University in 2012. Its basic idea comes from the simulation of natural flower self pollination and cross pollination. It is a new meta heuristic swarm intelligent random optimization technology. In order to simplify the calculation, it is assumed that each plant has only one flower and each flower has only one gamete. We can think that each gamete is a candidate solution in the solution space.

Through his research on flower pollination, Yang abstracted the following four rules:

1) Biological cross pollination is considered as the global detection behavior of the algorithm, and the pollinator realizes global pollination through Levy flight mechanism;

2) Abiotic self pollination is regarded as the local mining behavior of the algorithm, or local pollination;

3) The constancy of flowers can be regarded as the probability of reproduction, which is directly proportional to the similarity of two pollinated flowers;

4) The global and local pollination of flowers are regulated by the conversion probability p ∈ [0,1]. Due to the influence of physical proximity and wind, the conversion probability p is a very important parameter in the whole pollination activity. The experimental study on this parameter in reference [1] shows that P = 0.05 8 is more conducive to algorithm optimization.

Direct up steps (taking multivariate function optimization as an example):

Objective function: Min g = f (x1, X2, X3, X4......... XD)

Setting parameters: N (number of candidate solutions), iter (maximum number of iterations), p (conversion probability), lamda (Levy flight parameter)

Initialize the flower and randomly set an NXd matrix;

Calculate fitness, i.e. function value;

Obtain the optimal solution and the location of the optimal solution;

A cycle 1:1: iter

Cycle B

        if rand < p

Global pollination;

        else

Local pollination;

        end if

Update the flowers and fitness of the new generation (function variables and function values);

B cycle end

Obtain the optimal solution and optimal solution location of the new generation;

A cycle end

Global update formula: xi(t+1) = xi(t) + L(xi(t) - xbest(t)) l follows Levy distribution. For details, you can search cuckoo algorithm.

Local renewal formula: xi(t+1) = xi(t) + m(xj(t) - xk(t)) m is a random number uniformly distributed on [0,1]. xj and xk are two different individuals

2, Flower pollination algorithm based on t-distribution perturbation strategy and mutation strategy

(1) Chaotic map initializing individual position

(2) global search based on t-distributed perturbation strategy

(3) Local search based on mutation strategy

(4) algorithm implementation

 

2, Demo code

%__________________________________________
% fobj = @YourCostFunction
% dim = number of your variables
% Max_iteration = maximum number of generations
% SearchAgents_no = number of search agents
% lb=[lb1,lb2,...,lbn] where lbn is the lower bound of variable n
% ub=[ub1,ub2,...,ubn] where ubn is the upper bound of variable n
% If all the variables have equal lower bound you can just
% define lb and ub as two single number numbers

% To run ALO: [Best_score,Best_pos,cg_curve]=ALO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj)

% The Whale Optimization Algorithm
function [Leader_score,Leader_pos,Convergence_curve]=WOA(SearchAgents_no,Max_iter,lb,ub,dim,fobj,handles,value)

% initialize position vector and score for the leader
Leader_pos=zeros(1,dim);
Leader_score=inf; %change this to -inf for maximization problems


%Initialize the positions of search agents
Positions=initialization(SearchAgents_no,dim,ub,lb);

Convergence_curve=zeros(1,Max_iter);

t=0;% Loop counter

% Main loop
while t<Max_iter
    for i=1:size(Positions,1)
        
        % Return back the search agents that go beyond the boundaries of the search space
        Flag4ub=Positions(i,:)>ub;
        Flag4lb=Positions(i,:)<lb;
        Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
        
        % Calculate objective function for each search agent
        fitness=fobj(Positions(i,:));
        All_fitness(1,i)=fitness;
        
        % Update the leader
        if fitness<Leader_score % Change this to > for maximization problem
            Leader_score=fitness; % Update alpha
            Leader_pos=Positions(i,:);
        end
        
    end
    
    a=2-t*((2)/Max_iter); % a decreases linearly fron 2 to 0 in Eq. (2.3)
    
    % a2 linearly dicreases from -1 to -2 to calculate t in Eq. (3.12)
    a2=-1+t*((-1)/Max_iter);
    
    % Update the Position of search agents 
    for i=1:size(Positions,1)
        r1=rand(); % r1 is a random number in [0,1]
        r2=rand(); % r2 is a random number in [0,1]
        
        A=2*a*r1-a;  % Eq. (2.3) in the paper
        C=2*r2;      % Eq. (2.4) in the paper
        
        
        b=1;               %  parameters in Eq. (2.5)
        l=(a2-1)*rand+1;   %  parameters in Eq. (2.5)
        
        p = rand();        % p in Eq. (2.6)
        
        for j=1:size(Positions,2)
            
            if p<0.5   
                if abs(A)>=1
                    rand_leader_index = floor(SearchAgents_no*rand()+1);
                    X_rand = Positions(rand_leader_index, :);
                    D_X_rand=abs(C*X_rand(j)-Positions(i,j)); % Eq. (2.7)
                    Positions(i,j)=X_rand(j)-A*D_X_rand;      % Eq. (2.8)
                    
                elseif abs(A)<1
                    D_Leader=abs(C*Leader_pos(j)-Positions(i,j)); % Eq. (2.1)
                    Positions(i,j)=Leader_pos(j)-A*D_Leader;      % Eq. (2.2)
                end
                
            elseif p>=0.5
              
                distance2Leader=abs(Leader_pos(j)-Positions(i,j));
                % Eq. (2.5)
                Positions(i,j)=distance2Leader*exp(b.*l).*cos(l.*2*pi)+Leader_pos(j);
                
            end
            
        end
    end
    
    t=t+1;
    Convergence_curve(t)=Leader_score;
    
    if t>2
        line([t-1 t], [Convergence_curve(t-1) Convergence_curve(t)],'Color','b')
        xlabel('Iteration');
        ylabel('Best score obtained so far');        
        drawnow
    end
 
    
    set(handles.itertext,'String', ['The current iteration is ', num2str(t)])
    set(handles.optimumtext,'String', ['The current optimal value is ', num2str(Leader_score)])
    if value==1
        hold on
        scatter(t*ones(1,SearchAgents_no),All_fitness,'.','k')
    end
    
    
    
    
end

4, Simulation results

Table 1 basic information of test function

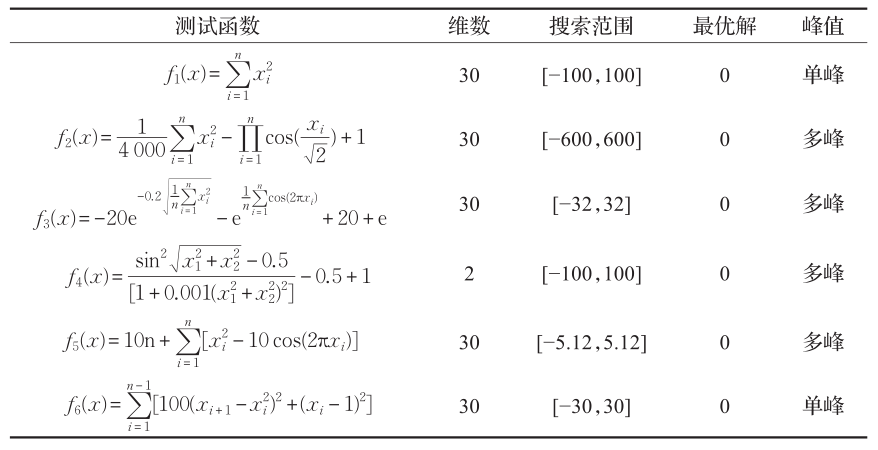
In order to verify the performance of the tMFPA algorithm proposed in this paper, each algorithm in the simulation experiment runs independently for 30 times, and the maximum number of iterations is set to 2000 times, taking 30 dimensions as an example.
The results are as follows: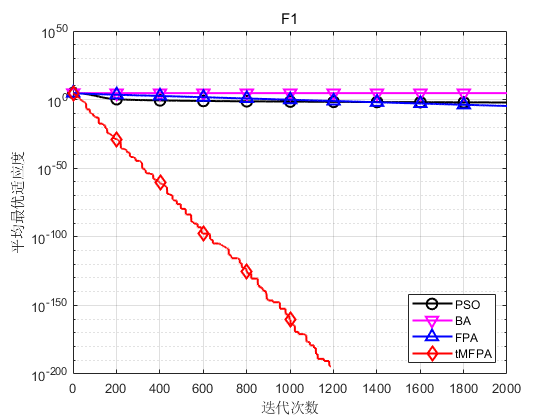

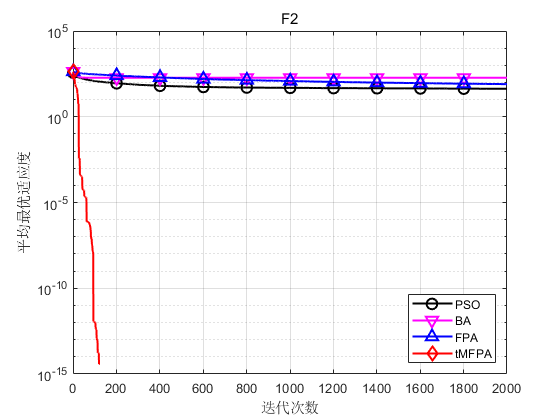
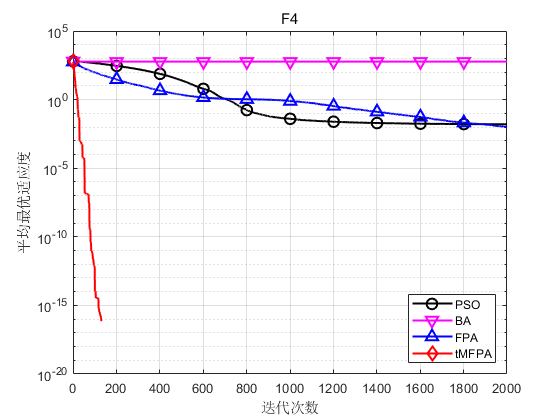
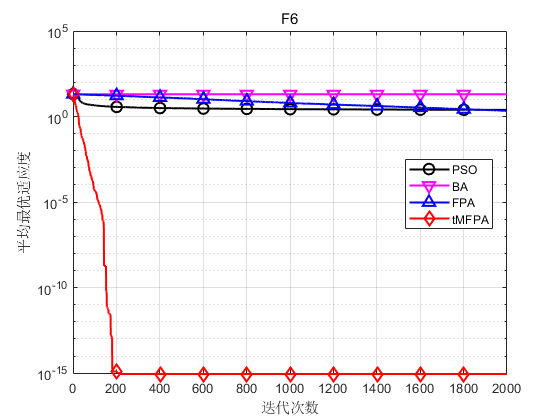
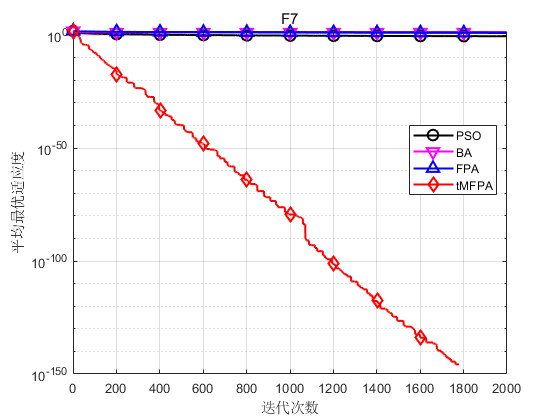
The results show that tMFPA has better optimization accuracy and convergence speed than FPA and other heuristic intelligent algorithms.  

5, References and codes private bloggers

[1] Ning Jieqiong, he Qing   Flower pollination algorithm based on t-distribution perturbation strategy and mutation strategy [J]. Small microcomputer system, 2021, 42 (1): 64-70