Design idea:
<(teaching-06) maximum number of addition and subtraction methods within 20 (optimized version 20220122 vs Python addition and subtraction method within 20) >The code can randomly generate up to addition questions and addition questions within x. A Xia tried to modify the code to make the list questions and quantity of "5 on / off" and "10 on / off".
Main solutions:
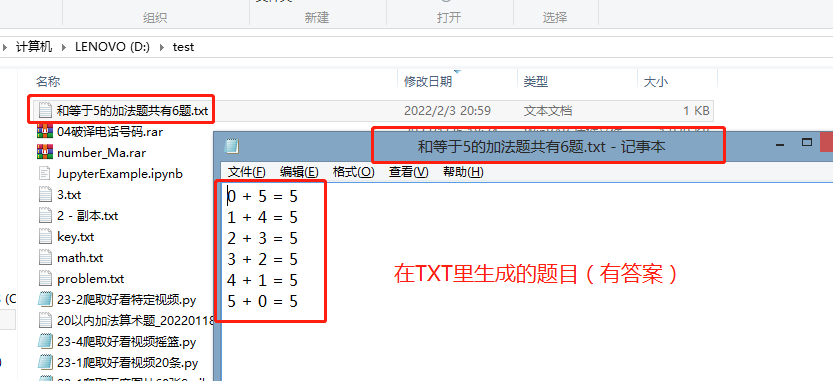
1. There are several addition questions with sum equal to 5: 0 + 5 = 5 , 1 + 4 = 5... (opening and closing of 5, opening and closing of 6, opening and closing of 10)
2. There are several subtraction questions with a difference equal to 5 (set the subtracted number to 10): 10-5=5 9-4=5 ……()
usage method:
1. Save the PY code in 'add subtract equals 5' Within py '

2. py code
# -*- coding: utf-8 -*-
"""
@author: Ma Qingxin
@file: Asha modification exercise
How many questions are there in addition questions with sum equal to 5.py
How many subtraction questions with a difference equal to 5(Set subtracted).py
@time: 2022/2/3 20:15
# Special note
1.There are two number addition questions with an answer equal to 5. There are several questions in total (within 5))?
2.How many questions are there for the two digit subtraction questions with an answer equal to 5?(Set subtracted)
"""
import random
from re import X
from tkinter import Y
#Set questions:
choice=int(input('-----------------------------------\n'
'You need X Integer addition or integer subtraction within?\n'
'1.Add 2.Subtraction (please enter serial number)\n'
'------------------------------------\n'))
if choice==1: #addition
plusAnswer = int(input('Please enter the answer of addition z((≥0)): \n'))# Enter the number of answers to the addition question, such as adding. List the total number of questions with the answer of 5
regNum = int(input('Please enter the number of formulas to be generated:\n'))# Enter the required quantity
# Generate a list from 0 to the arithmetic maximum sum. Because the range function package does not include the right, if you want to include the arithmetic maximum sum, you must + 1
# The range function starts from 0, so that the list elements are consistent with the list index, reducing the difficulty of the algorithm
numList = [x for x in range(0,plusAnswer+1)]# Establish an integer list. Assume that summax = 20, summax + 1 equals 21, but the actual range is 1-20. Ensure that the list index is consistent with the list elements
# The resultList list is used to save the compliance arithmetic expression of the last demand quantity
resultList = []# List of stored results
# Cycle from the second element of the list to the last element of the list
for x in numList[0:]:# 0 equals the number 1
# Cycle from the x-th element of the list to the last element of the list
for y in numList[x:]:
# In the first addition, xy is equal and X + y < 20. At the beginning of the list element, there are two equal elements. Because the addition exchange law will produce repetition, it is distinguished separately
if x+y ==plusAnswer and y!=0:
tempStr = str(x) + ' + ' + str(y) + ' = ' #Addition type 1 x+y = (x=y)
resultList.append((tempStr, (x+y)))# For questions with answers, such as 2 + 2 = 4, lines 70 and 72, select 0 or 1 to print the results with or without answers
tempStr = str(y) + ' + ' + str(x) + ' = ' #Addition type 1 x+y = (x=y)
resultList.append((tempStr, (y+x)))# Questions with answers, such as 2 + 2 = 4, line 70 and
selectList = []# Selection list
if regNum > len(resultList):#If (quantity of input formula) is greater than (quantity of result list)#If the number of input questions is greater than the actual demand, shuffle the cards,
print(f'Your demand is greater than the maximum formula generation quantity! The maximum number of generated formulas is{len(resultList)}') # Add the statistical value of the maximum non repeating formula. If the number of questions entered is greater than the number of lists in which the results are stored, add LEN to the list
i = len(resultList)# The number of i is equal to the number of lists in which the results are stored
for _ in resultList:# The value is in the list of cyclic storage results
# selectList = random.sample(resultList,i)
selectList.append(_) #To select the list, you need to add the contents of the circular storage result list
selectList.sort() #In positive order from small to large, 0 + 5 = 5, 1 + 4 = 5
# selectList.sort(reverse=True) #Flashback from large to small 5 + 0 = 5 4 + 1 = 5
# for _ in selectList:
# # Optional printing with and without answers 8
# print(_[0])# Without answer 5
# # print(f'{_[0]}{_[1]}')# With answers
# else:#If the number of input questions is less than the actual demand, the code will be automatically selected at random and will not be sorted,
# i = regNum
# selectList = random.sample(resultList,i)
# for _ in selectList:
# # You can print with or without answers
# print(_[0])# No answer
# # print(f'{_[0]}{_[1]}')# With answer 2
print(f'The number of questions that generate non repeated addition formulas{len(selectList)}')# Select the number of lists
print(f'The limited number of maximum unrepeatable addition formulas{len(resultList)}')# Number of result lists
# Save as TXT file (in the default open folder, manually copy to Word 1)
str_title = 'Sum equals%d The addition questions are common%d topic.txt' % (plusAnswer, len(resultList)) # Save file name 60
with open(str_title,'w') as f:# Open TXT file
for a in selectList:# #Loop through the contents of the answer 878
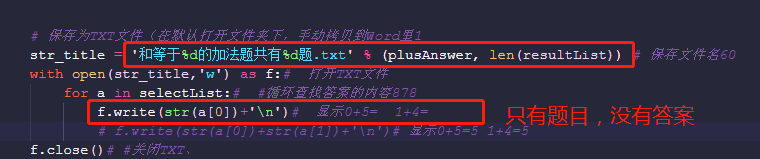
# f.write(str(a[0])+'\n')# Display 0 + 5 = 1 + 4=
f.write(str(a[0])+str(a[1])+'\n')# Display 0 + 5 = 5 1 + 4 = 5
f.close()# #Turn off TXT
elif choice==2: # subtraction
subAnswer = int(input('Please enter the answer you want to subtract: '))# Enter the number of answers you want for the subtraction question, such as 5. For example, how many questions are there for the question with the answer of 5
sumMax=int(input('Please enter the number of subtracted (maximum): '))# For example, 10-5 = 5, 9-4 = 5, input the first number X10, 9 of the subtraction question
regNum = int(input('Please enter the number of formulas to be generated: '))# Enter the required quantity
# Generate a list from 0 to the arithmetic maximum sum. Because the range function package does not include the right, if you want to include the arithmetic maximum sum, you must + 1
# The range function starts from 0, so that the list elements are consistent with the list index, reducing the difficulty of the algorithm
numList = [x for x in range(0,sumMax+1)]# Establish an integer list with a value range of 5-10
# The resultList list is used to save the compliance arithmetic expression of the last demand quantity
resultList = []# List of stored results
# Cycle from the second element of the list to the last element of the list
for x in numList[0:]:# 0 equals the number 1
# Cycle from the x-th element of the list to the last element of the list
for y in numList[x:]:
# The first subtraction, xy is not equal, x > y
if x - y == subAnswer and y!=x:# The first condition of y-x is x+y < 20, and X is not equal to y (equal to 0)
tempStr = str(x) + ' - ' + str(y) + ' = '#Subtraction type 1 y-x=
resultList.append((tempStr, (x-y)))# Questions with answers, such as 3-2 = 1,
elif y - x ==subAnswer: #Subtraction conditions include y+x less than 20 and Y - x > 0
tempStr = str(y) + ' - ' + str(x) + ' = '#Subtraction type 2 y-x = (second condition of y-x Y-X > 0)
resultList.append((tempStr, (y-x)))# Questions with answers, such as 2 + 2 = 4,
selectList = []# Selection list
if regNum > len(resultList):#If (quantity of input formula) is greater than (quantity of result list)#If the number of input questions is greater than the actual demand, shuffle the cards,
print(f'Your demand is greater than the maximum formula generation quantity! The maximum number of generated formulas is{len(resultList)}') # Add the statistical value of the maximum non repeating formula. If the number of questions entered is greater than the number of lists in which the results are stored, add LEN to the list
i = len(resultList)# The number of i is equal to the number of lists in which the results are stored
for _ in resultList:# The value is in the list of cyclic storage results
# selectList = random.sample(resultList,i)
selectList.append(_) #To select the list, you need to add the contents of the circular storage result list
# At this time, it is arranged in positive order from small to large, 5 - 0 = 5, 6 - 1 = 5
sorted(selectList)#Positive order from small to large 5 - 0 = 5 6 - 1 = 5
# reversed(selectList)#Positive order from small to large 5 - 0 = 5 6 - 1 = 5
for _ in selectList:
# Optional printing with and without answers 8
# print(_[0])# No answer
print(f'{_[0]}{_[1]}')# With answers
else:#If the number of input questions is less than the actual demand, the code will be automatically selected at random and will not be sorted,
i = regNum
selectList = random.sample(resultList,i)
for _ in selectList:
# You can print with or without answers
# print(_[0])# No answer
print(f'{_[0]}{_[1]}')# With answer 2
# Verify the number of generated formulas 70
print(f'The number of questions that generate non repeated subtraction formulas{len(selectList)}')# Select the number of lists
print(f'The maximum number of non repeating subtractions{len(resultList)}')# Number of result lists
# Save as TXT file (in the default open folder, manually copy to Word 1)
str_title = 'Difference equals%d Subtraction (subtraction)%d)share%d topic.txt' % (subAnswer, sumMax,len(resultList))
with open(str_title,'w') as f:# Open TXT file
for a in selectList:# #Cycle through the contents of the answer 8
# f.write(str(a[0])+'\n')# Display 10-5 = 9-5=
f.write(str(a[0])+str(a[1])+'\n')# Display 10-5 = 5 9-5 = 5
f.close()# #Turn off TXT
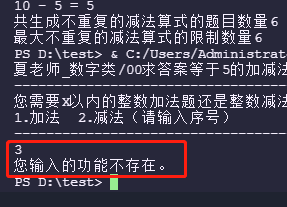
else:
print('The function you entered does not exist.')
3. Select 1 addition question to run
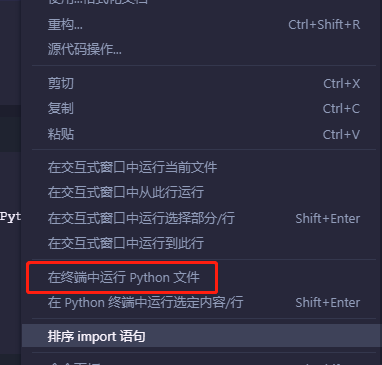
4. Choose addition or subtraction
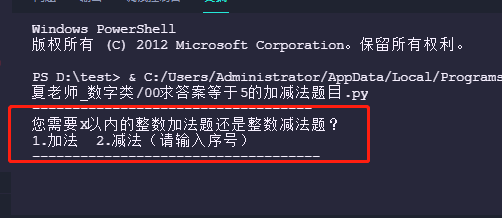
5. Select the addition question and enter 1 + enter

6. The sum of addition is equal to 5 , enter
h 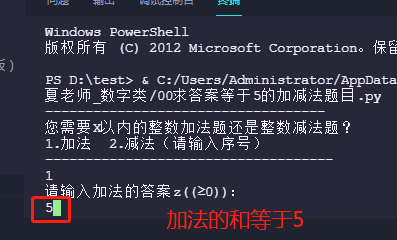
7. Enter the desired number of questions (three digits) at will, but only about 6 questions will be retained in the end

8. In the end, it is equal to 5, generating 6 non repeated addition questions and 6 maximum non repeated addition questions,

9. Generated code in TXT format
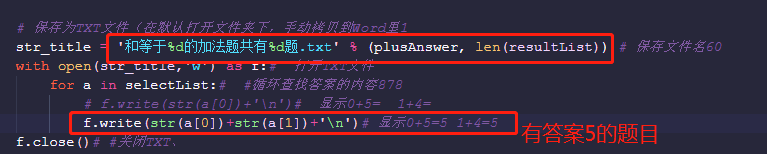
10. Questions in TXT (another question + answer 5)
11. Questions in TXT (only questions, no answers 5)
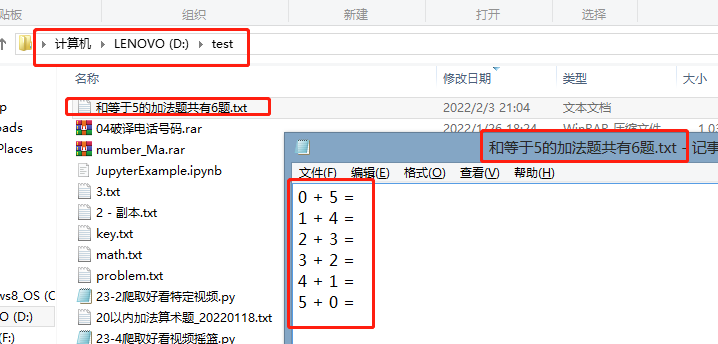
12. Choose 2 subtraction questions to run


13. List questions with a difference of 5
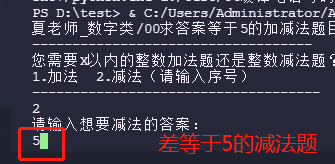
14. Set the range of subtraction: for example, 6-1 = 5, 7-2 = 5... Choose the largest subtraction. Here is the maximum number of subtraction questions within 10. The final answer is equal to 5

15. The number of questions is still entered casually. Anyway, only the actual number of questions will be generated in the end

The number of questions with subtraction = 5 within 16.10 is 6
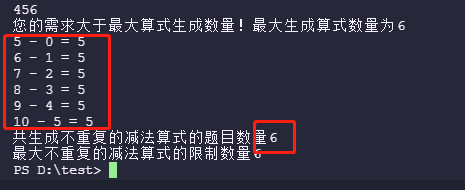
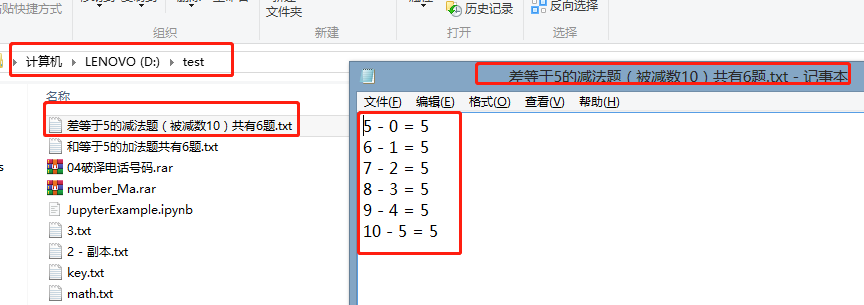
17. Subtraction TXT # style 1: there are questions and answers 5
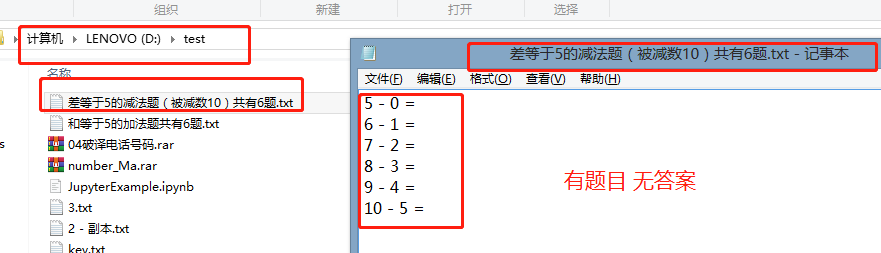
18. Subtraction TXT# style 2: there are questions but no answers

19. If you enter numbers or Chinese characters other than 1 and 2, this option is not displayed.

Long term objectives:
This code design is mainly to prepare for the problem type of division and combination of mathematics in large class within 10. Through fine-tuning the code content, we can further interpret and understand the content of Mr. Ma's source code, so as to provide the basis for subsequent design. Thank you, Mr. Ma.