1, Introduction

1 concept of particle swarm optimization algorithm
Particle swarm optimization (PSO) is an evolutionary computing technology. From the study of predation behavior of birds. The basic idea of particle swarm optimization algorithm is to find the optimal solution through the cooperation and information sharing among individuals in the group
The advantage of PSO is that it is simple and easy to implement, and there is no adjustment of many parameters. At present, it has been widely used in function optimization, neural network training, fuzzy system control and other application fields of genetic algorithm.

2 particle swarm optimization analysis
2.1 basic ideas
Particle swarm optimization (PSO) simulates birds in a flock of birds by designing a massless particle. The particle has only two attributes: speed and position. Speed represents the speed of movement and position represents the direction of movement. Each particle searches for the optimal solution separately in the search space, records it as the current individual extreme value, shares the individual extreme value with other particles in the whole particle swarm, and finds the optimal individual extreme value as the current global optimal solution of the whole particle swarm, All particles in the particle swarm adjust their speed and position according to the current individual extreme value found by themselves and the current global optimal solution shared by the whole particle swarm. The following dynamic diagram vividly shows the process of PSO algorithm:

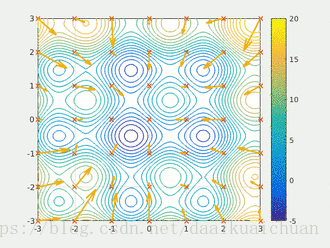
2 update rules
PSO is initialized as a group of random particles (random solutions). Then the optimal solution is found through iteration. In each iteration, the particle updates itself by tracking two "extreme values" (pbest, gbest). After finding these two optimal values, the particle updates its speed and position through the following formula.

The first part of formula (1) is called [memory item], which represents the influence of the last speed and direction; The second part of formula (1) is called [self cognitive item], which is a vector from the current point to the best point of the particle itself, indicating that the action of the particle comes from its own experience; The third part of formula (1) is called [group cognition item], which is a vector from the current point to the best point of the population, reflecting the cooperation and knowledge sharing among particles. Particles determine the next movement through their own experience and the best experience of their companions. Based on the above two formulas, the standard form of PSO is formed.

Formulas (2) and (3) are considered as standard PSO algorithms.
3 PSO algorithm flow and pseudo code

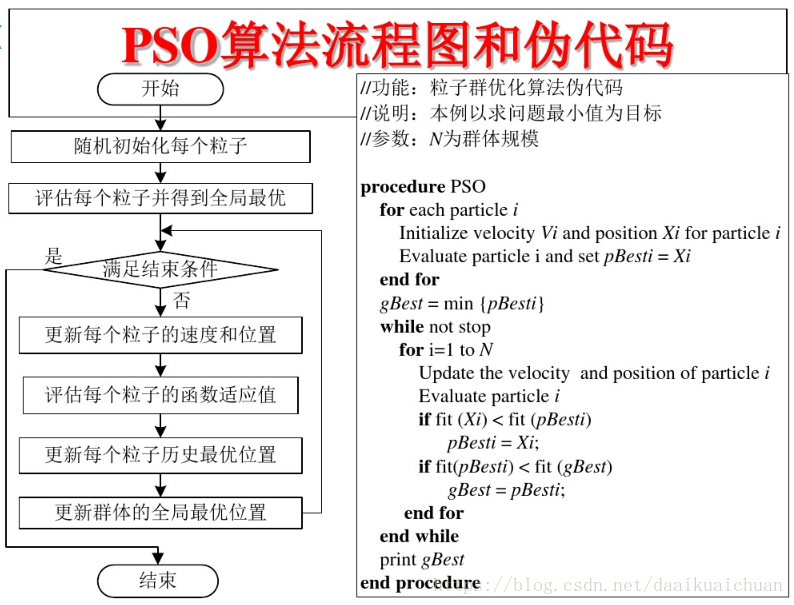
2, Source code

%_________________________________________________________________________%
% be based on Tent Improved particle swarm optimization algorithm based on chaotic mapping             %
%_________________________________________________________________________%

% usage method
%__________________________________________
% fobj = @YourCostFunction        Set fitness function
% dim = number of your variables   Set dimension
% Max_iteration = maximum number of generations Set the maximum number of iterations
% SearchAgents_no = number of search agents   Population number
% lb=[lb1,lb2,...,lbn] where lbn is the lower bound of variable n  Lower boundary of variable
% ub=[ub1,ub2,...,ubn] where ubn is the upper bound of variable n   Upper boundary of variable
clear all
clc
close all
SearchAgents_no=10; % Population number
Function_name='F4'; % Name of the test function that can be from F1 to F23 (Table 1,2,3 in the paper) Set fitness function
Vmax=5;%Upper speed limit
Vmin=-5;%Lower speed limit
Max_iteration=50;% Evolution times
a=0.5;%Chaos coefficient
c1 = 1.49445;%Individual learning rate
c2 = 1.49445;%Group learning rate
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);  %Setting boundaries and optimizing functions
%lb%Particle minimum
%ub%Particle maximum
%dim%Particle dimension
[Best_pos_tent,pso_curve_tent,Best_score_tent]=psoNew(SearchAgents_no,Max_iteration,lb,ub,dim,fobj,Vmax,Vmin,a,c1,c2); %tent Chaotic particle swarm optimization
[Best_pos,pso_curve,Best_score]=pso(SearchAgents_no,Max_iteration,lb,ub,dim,fobj,Vmax,Vmin,c1,c2); %Elementary particle swarm optimization

figure('Position',[269   240   660   290])
%Draw search space
subplot(1,2,1);
func_plot(Function_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])

%Draw objective space
subplot(1,2,2);
plot(pso_curve_tent,'Color','r')
hold on;
plot(pso_curve,'Color','b')
title('Objective space')
xlabel('Iteration');
ylabel('Best score obtained so far');

axis tight
grid on
box on
 
%
display(['The best solution obtained by Tent Chaotic strategy PSO is : ', num2str(Best_pos_tent)]);
display(['The best optimal value of the objective funciton found by Tent Chaotic strategy PSO is : ', num2str(Best_score_tent)]);
display(['The best solution obtained by PSO is : ', num2str(Best_pos)]);
display(['The best optimal value of the objective funciton found by Tent Chaotic strategy PSO is : ', num2str(Best_score)]);

3, Operation results

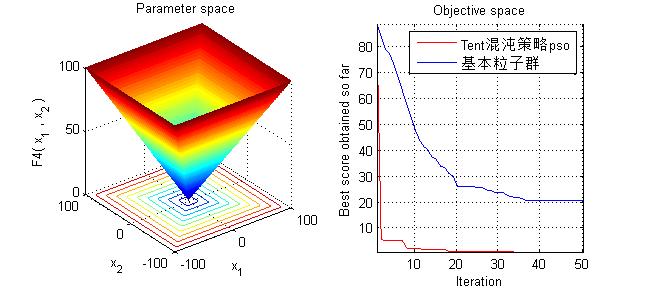
4, Remarks

Version: 2014a