1, Introduction
1 overview of genetic algorithm
Genetic Algorithm (GA) is a part of evolutionary computation. It is a computational model that simulates the biological evolution process of Darwin's genetic selection and natural elimination. It is a method to search the optimal solution by simulating the natural evolution process. The algorithm is simple, universal, robust and suitable for parallel processing.
2 characteristics and application of genetic algorithm
Genetic algorithm is a kind of robust search algorithm that can be used for complex system optimization. Compared with the traditional optimization algorithm, it has the following characteristics:
(1) Take the code of decision variable as the operation object. Traditional optimization algorithms often directly use the actual value of decision variables itself for optimization calculation, but genetic algorithm uses some form of coding of decision variables as the operation object. This coding method of decision variables enables us to learn from the concepts of chromosome and gene in biology in optimization calculation, imitate the genetic and evolutionary incentives of organisms in nature, and easily apply genetic operators.
(2) Directly take fitness as search information. The traditional optimization algorithm not only needs to use the value of the objective function, but also the search process is often constrained by the continuity of the objective function. It may also need to meet the requirement that "the derivative of the objective function must exist" to determine the search direction. Genetic algorithm only uses the fitness function value transformed from the objective function value to determine the further search range, without other auxiliary information such as the derivative value of the objective function. Directly using the objective function value or individual fitness value can also focus the search range into the search space with higher fitness, so as to improve the search efficiency.
(3) Using the search information of multiple points has implicit parallelism. The traditional optimization algorithm is often an iterative search process starting from an initial point in the solution space. The search information provided by a single point is not much, so the search efficiency is not high, and it may fall into local optimal solution and stop; Genetic algorithm starts the search process of the optimal solution from the initial population composed of many individuals, rather than from a single individual. The, selection, crossover, mutation and other operations on the initial population produce a new generation of population, including a lot of population information. This information can avoid searching some unnecessary points, so as to avoid falling into local optimization and gradually approach the global optimal solution.
(4) Use probabilistic search instead of deterministic rules. Traditional optimization algorithms often use deterministic search methods. The transfer from one search point to another has a certain transfer direction and transfer relationship. This certainty may make the search less than the optimal store, which limits the application scope of the algorithm. Genetic algorithm is an adaptive search technology. Its selection, crossover, mutation and other operations are carried out in a probabilistic way, which increases the flexibility of the search process, and can converge to the optimal solution with a large probability. It has a good ability of global optimization. However, crossover probability, mutation probability and other parameters will also affect the search results and search efficiency of the algorithm, so how to select the parameters of genetic algorithm is a more important problem in its application.
To sum up, because the overall search strategy and optimization search mode of genetic algorithm do not rely on gradient information or other auxiliary knowledge, and only need to solve the objective function and corresponding fitness function affecting the search direction, genetic algorithm provides a general framework for solving complex system problems. It depends on various kinds of optimization problems and has strong robustness to various fields of optimization and control
, robotics, image processing (image restoration, image edge feature extraction...), artificial life, genetic programming, machine learning.
3 basic flow and implementation technology of genetic algorithm
Simple genetic algorithms (SGA) only uses three genetic operators: selection operator, crossover operator and mutation operator. The evolution process is simple and is the basis of other genetic algorithms.
3.1 basic flow of genetic algorithm
Generating a number of initial groups encoded by a certain length (the length is related to the accuracy of the problem to be solved) in a random manner;
Each individual is evaluated by fitness function. Individuals with high fitness value are selected to participate in genetic operation, and individuals with low fitness are eliminated;
A new generation of population is formed by the collection of individuals through genetic operation (replication, crossover and mutation) until the stopping criterion is met (evolutionary algebra gen > =?);
The best realized individual in the offspring is taken as the execution result of genetic algorithm.
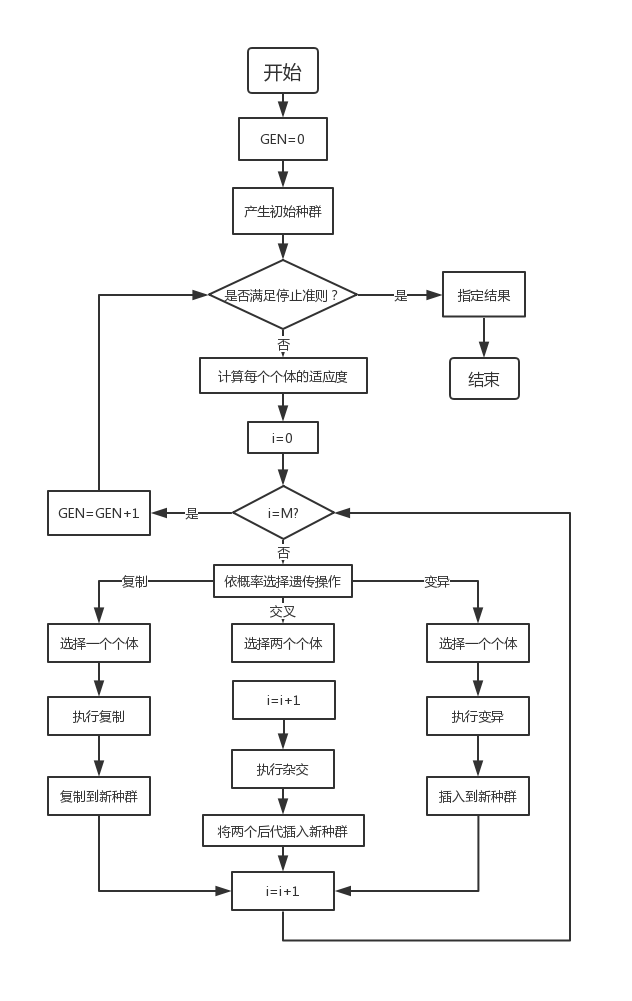
Where GEN is the current algebra; M is the population size, and i represents the population number.
3.2 implementation technology of genetic algorithm
Basic genetic algorithm (SGA) consists of coding, fitness function, genetic operators (selection, crossover, mutation) and operating parameters.
3.2.1 coding
(1) Binary coding
The length of binary coded string is related to the accuracy of the problem. It is necessary to ensure that every individual in the solution space can be encoded.
Advantages: the operation of encoding and decoding is simple, and the inheritance and crossover are easy to realize
Disadvantages: large length
(2) Other coding methods
Gray code, floating point code, symbol code, multi parameter code, etc
3.2.2 fitness function
The fitness function should effectively reflect the gap between each chromosome and the chromosome of the optimal solution of the problem.
3.2.3 selection operator

3.2.4 crossover operator
Cross operation refers to the exchange of some genes between two paired chromosomes in some way, so as to form two new individuals; Crossover operation is an important feature that distinguishes genetic algorithm from other evolutionary algorithms. It is the main method to generate new individuals. Before crossing, individuals in the group need to be paired. Generally, the principle of random pairing is adopted.
Common crossing methods:
Single point intersection
Double point crossing (multi-point crossing, the more crossing points, the greater the possibility of individual structure damage, and multi-point crossing is generally not adopted)
Uniform crossing
Arithmetic Crossover
3.2.5 mutation operator
Mutation operation in genetic algorithm refers to replacing the gene value of some loci in the individual chromosome coding string with other alleles of the locus, so as to form a new individual.
In terms of the ability to generate new individuals in the operation process of genetic algorithm, crossover operation is the main method to generate new individuals, which determines the global search ability of genetic algorithm; Mutation operation is only an auxiliary method to generate new individuals, but it is also an essential operation step, which determines the local search ability of genetic algorithm. The combination of crossover operator and mutation operator completes the global search and local search of the search space, so that the genetic algorithm can complete the optimization process of the optimization problem with good search performance.
3.2.6 operating parameters

4 basic principle of genetic algorithm
4.1 mode theorem

4.2 building block assumptions
Patterns with low order, short definition length and fitness value higher than the average fitness value of the population are called gene blocks or building blocks.
Building block hypothesis: individual gene blocks can be spliced together through the action of genetic operators such as selection, crossover and mutation to form individual coding strings with higher fitness.
The building block hypothesis illustrates the basic idea of solving various problems with genetic algorithm, that is, better solutions can be produced by directly splicing the building blocks together.
2, Source code
function varargout = gaGui(varargin)
% GAGUI M-file for gaGui.fig
% GAGUI, by itself, creates a new GAGUI or raises the existing
% singleton*.
%
% H = GAGUI returns the handle to a new GAGUI or the handle to
% the existing singleton*.
%
% GAGUI('CALLBACK',hObject,eventData,handles,...) calls the local
% function named CALLBACK in GAGUI.M with the given input arguments.
%
% GAGUI('Property','Value',...) creates a new GAGUI or raises the
% existing singleton*. Starting from the left, property value pairs are
% applied to the GUI before gaGui_OpeningFunction gets called. An
% unrecognized property name or invalid value makes property application
% stop. All inputs are passed to gaGui_OpeningFcn via varargin.
%
% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one
% instance to run (singleton)".
%
% See also: GUIDE, GUIDATA, GUIHANDLES
% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name', mfilename, ...
'gui_Singleton', gui_Singleton, ...
'gui_OpeningFcn', @gaGui_OpeningFcn, ...
'gui_OutputFcn', @gaGui_OutputFcn, ...
'gui_LayoutFcn', [] , ...
'gui_Callback', []);
if nargin && ischar(varargin{1})
gui_State.gui_Callback = str2func(varargin{1});
end
if nargout
[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
gui_mainfcn(gui_State, varargin{:});
end
% End initialization code - DO NOT EDIT
% --- Executes just before gaGui is made visible.
function gaGui_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% varargin command line arguments to gaGui (see VARARGIN)
% Choose default command line output for gaGui
handles.output = hObject;
% Update handles structure
guidata(hObject, handles);
% UIWAIT makes gaGui wait for user response (see UIRESUME)
% uiwait(handles.figure1);
% --- Outputs from this function are returned to the command line.
function varargout = gaGui_OutputFcn(hObject, eventdata, handles)
% varargout cell array for returning output args (see VARARGOUT);
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% Get default command line output from handles structure
varargout{1} = handles.output;
function EditCityNumber_Callback(hObject, eventdata, handles)
% hObject handle to EditCityNumber (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% Hints: get(hObject,'String') returns contents of EditCityNumber as text
% str2double(get(hObject,'String')) returns contents of EditCityNumber as a double
% --- Executes during object creation, after setting all properties.
function EditCityNumber_CreateFcn(hObject, eventdata, handles)
% hObject handle to EditCityNumber (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles empty - handles not created until after all CreateFcns called
% Hint: edit controls usually have a white background on Windows.
% See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
function edit3_Callback(hObject, eventdata, handles)
% hObject handle to edit3 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% Hints: get(hObject,'String') returns contents of edit3 as text
% str2double(get(hObject,'String')) returns contents of edit3 as a double
% --- Executes during object creation, after setting all properties.
function edit3_CreateFcn(hObject, eventdata, handles)
% hObject handle to edit3 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles empty - handles not created until after all CreateFcns called
% Hint: edit controls usually have a white background on Windows.
% See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
function editInitialGroup_Callback(hObject, eventdata, handles)
% hObject handle to editInitialGroup (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% Hints: get(hObject,'String') returns contents of editInitialGroup as text
% str2double(get(hObject,'String')) returns contents of editInitialGroup as a double
% --- Executes during object creation, after setting all properties.
function editInitialGroup_CreateFcn(hObject, eventdata, handles)
% hObject handle to editInitialGroup (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles empty - handles not created until after all CreateFcns called
% Hint: edit controls usually have a white background on Windows.
% See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
function EditCrossOver_Callback(hObject, eventdata, handles)
% hObject handle to EditCrossOver (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% Hints: get(hObject,'String') returns contents of EditCrossOver as text
% str2double(get(hObject,'String')) returns contents of EditCrossOver as a double
% --- Executes during object creation, after setting all properties.
function EditCrossOver_CreateFcn(hObject, eventdata, handles)
% hObject handle to EditCrossOver (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles empty - handles not created until after all CreateFcns called
% Hint: edit controls usually have a white background on Windows.
% See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
function edit6_Callback(hObject, eventdata, handles)
% hObject handle to edit6 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% Hints: get(hObject,'String') returns contents of edit6 as text
% str2double(get(hObject,'String')) returns contents of edit6 as a double
% --- Executes during object creation, after setting all properties.
function edit6_CreateFcn(hObject, eventdata, handles)
% hObject handle to edit6 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles empty - handles not created until after all CreateFcns called
% Hint: edit controls usually have a white background on Windows.
% See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
% --- Executes on button press in GenerateInitialCitiesButton.
function GenerateInitialCitiesButton_Callback(hObject, eventdata, handles)
% hObject handle to GenerateInitialCitiesButton (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
str1=char(get(handles.EditCityNumber,'string'));
global N
N=str2num(str1);
%Generate random city
global cities;
if(~isempty(cities))
cla;
end
cities=round(100*rand(N,2));
axes(handles.CityMap);
for k=1:N
if(k~=1)
hold on
end
plot(cities(k,1),cities(k,2),'bo');
end
3, Operation results
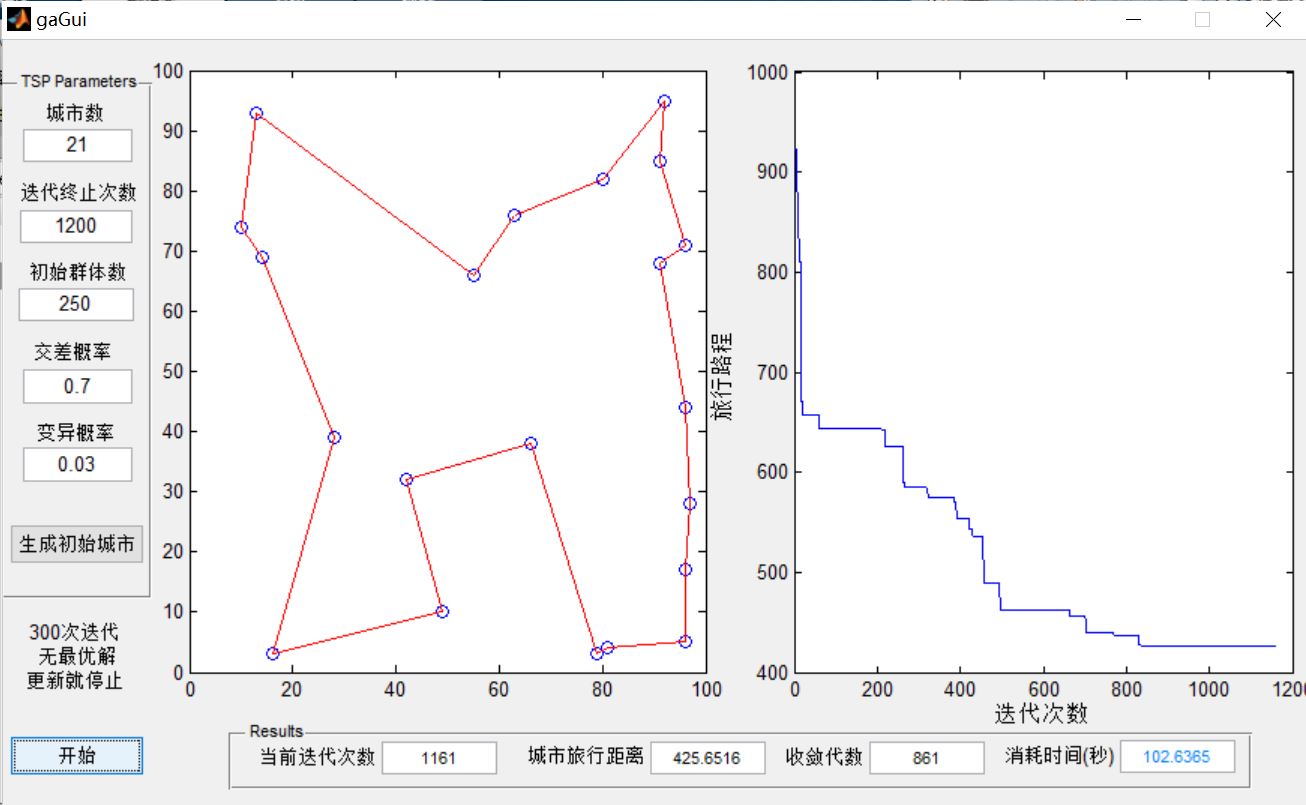
4, Remarks
edition; 2014a