1, Case description

Three classic images (lena, pepper and barbara) are added with Gaussian noise, multiplicative noise and salt and pepper noise respectively. Gaussian white noise: the mean value is 0 and the variance is 0.05. Salt and pepper noise: noise density 0.10. Multiplicative noise: here is the noise with uniformly distributed mean value of 0 and variance of 0.10. (1) Use mean filter and median filter to test, get and analyze the denoising effect; (2) Use Gaussian low-pass filter and Butterworth filter to test, get and analyze the denoising effect; (3) Use PCA to test, get and analyze the denoising effect; (4) The wavelet transform can be used for testing, such as' db 'wavelet and' sym 'wavelet, or you can choose some wavelet functions to get the denoising effect and analyze it; (5) Choose some methods by yourself, get the denoising effect and analyze it.

2, Introduction to image denoising and filtering

1 image denoising
1.1 definition of image noise
Noise is an important factor that interferes with the visual effect of image. Image denoising refers to the process of reducing noise in image. There are three kinds of noise classification: additive noise, multiplicative noise and quantization noise. We use f(x,y) to represent the image, g(x,y) to represent the image signal, and n(x,y) to represent the noise.
Image denoising refers to the process of reducing noise in digital images. The digital image in reality is often affected by the noise interference of imaging equipment and external environment in the process of digitization and transmission, which is called noisy image or noisy image. Denoising is an important content in image processing research. In the process of image acquisition, transmission, transmission, reception, replication and output, noise is often generated, among which salt and pepper noise is a common noise, which belongs to additive noise.

1.2 image noise source
(1) During image acquisition
In the process of image acquisition by image sensor CCD and CMOS, various noises will be introduced due to the influence of sensor material properties, working environment, electronic components and circuit structure.
(2) In the process of image signal transmission
Due to the imperfection of transmission media and recording equipment, digital images are often polluted by a variety of noise in the process of transmission and recording.

1.3 noise classification
Noise can be classified in different forms according to different classification standards:
Based on the causes: internal noise, external noise.
Based on the relationship between noise and signal:
Additive noise: additive noise is not related to image signal strength. This kind of image g with noise can be regarded as the sum of ideal noiseless image f and noise n:
g = f + n；
Multiplicative voice: multiplicative noise is related to the image signal and often changes with the change of the image signal. The noise generated by the change of the carrier carrying each pixel information is modulated by the information itself. In some cases, for example, the signal change is small and the noise is small. For the convenience of analysis and processing, multiplicative noise is often regarded as additive noise, and it is always assumed that signal and noise are statistically independent of each other.
g = f + f*n
According to the probability density function based on Statistics:
It is more important, mainly because the introduction of mathematical model is helpful to remove noise by mathematical means. In different scenes, the application methods of noise are different. Because under certain external conditions, the probability density function (statistical result) of the image original image under noise (when there is no noise) obeys a certain distribution function, it is classified as the corresponding noise. The noise classification based on the statistical probability density function and its elimination method will be described in detail below.

1.4 classification of image denoising algorithms
(1) Spatial domain filtering
Spatial filtering is to directly perform data operation on the original image and process the gray value of pixels. Common spatial domain image denoising algorithms include neighborhood average method, median filter, low-pass filter and so on.
(2) Transform domain filtering
Image transform domain denoising method is to transform the image, convert the image from spatial domain to transform domain, process the transform coefficients in the transform domain, and then inverse transform the image from transform domain to spatial domain to remove the image voice. There are many methods to transform images from spatial domain to transform domain, such as Fourier transform, Walsh Hadamard transform, cosine transform, K-L transform and wavelet transform. Fourier transform and wavelet transform are common transform methods for image denoising.
(3) Partial differential equation
Partial differential equation is an image processing method rising in recent years. It is mainly aimed at low-level image processing and has achieved good results. Partial differential equation has the characteristics of anisotropy. When applied in image denoising, it can remove the noise and maintain the edge well. The application of partial differential equations can be divided into two categories: one is the basic iterative format, which makes the image approach the desired effect gradually through the update over time. The representative of this algorithm is Perona and Malik's equation, and the follow-up work after its improvement. This method has a large selection space in determining the diffusion coefficient. It has the function of backward diffusion while forward diffusion. Therefore, it has the ability to smooth the image and sharpen the edge. Partial differential equations have achieved good results in image processing with low noise density, but the denoising effect is not good when processing images with high noise density, and the processing time is much higher.
(4) Variational method
Another image denoising method using mathematics is to determine the energy function of the image based on the idea of variational method, and make the image reach a smooth state by minimizing the energy function. Now the fully variational TV model, which is widely used, is this kind. The key of this kind of method is to find an appropriate energy equation to ensure the stability of evolution and obtain ideal results.
Morphological noise filter can be used to filter noise by combining opening and closing. Firstly, the noisy image can be opened, and the structure element matrix can be selected to be larger than the noise size. Therefore, the result of opening operation is to remove the background noise; Then close the image obtained in the previous step to remove the noise on the image. Therefore, it can be seen that the applicable image type of this method is that the object size in the image is relatively large and there are no small details, so the denoising effect of this kind of image will be better.

2-value filtering
(1) Concept:

(2) Principle explanation:

3 mean filtering
Mean filtering refers to the pixel value of any point, which is the mean of the surrounding N \times M pixel values. For example, in the following figure, the pixel value of the red dot is the sum of the pixel values of the surrounding blue background area, divided by 25, 25=5\times5 is the size of the blue area.

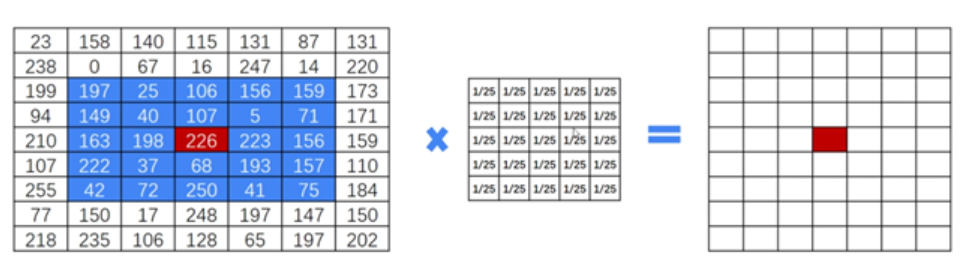
The detailed calculation method of mean filtering is shown in the figure below:

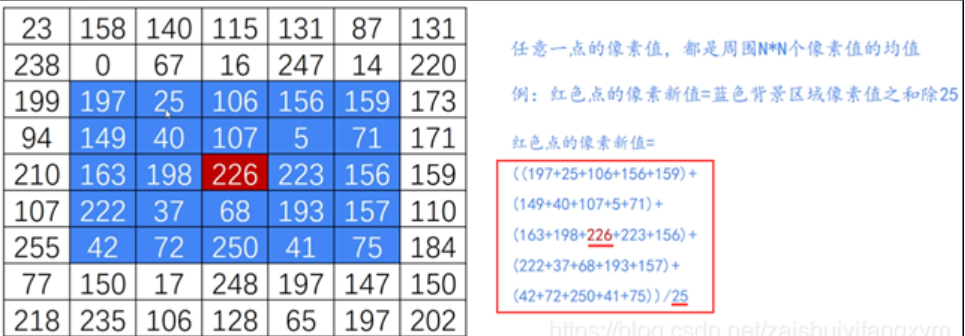
The matrix of 5\times5 is called kernel. For the pixels in the original image, the kernel is used to process and obtain the result image, as shown in the following figure:


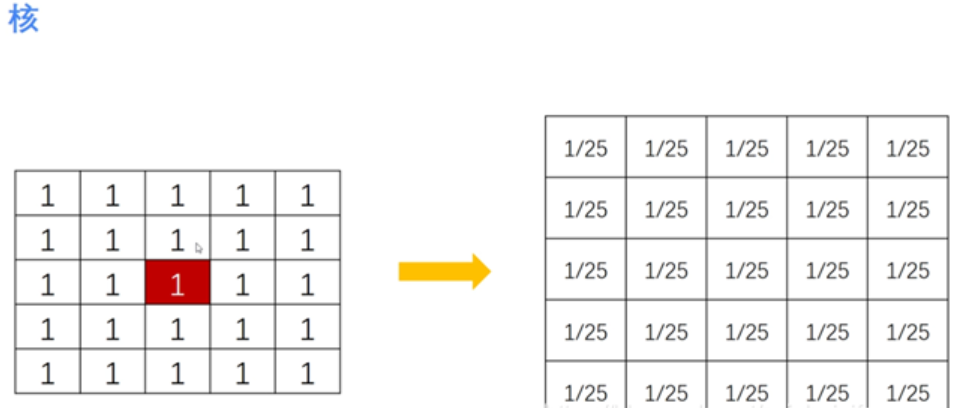
Extracting 1 / 25 can convert the core into the following form:

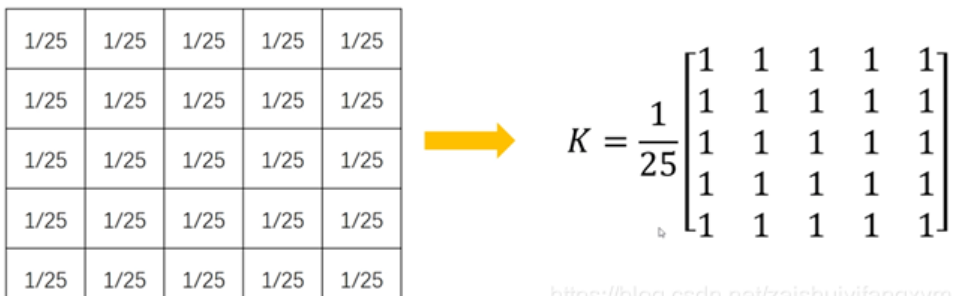
4 Lee filtering

3, Partial source code

function varargout = main(varargin)
% MAIN MATLAB code for main.fig
%      MAIN, by itself, creates a new MAIN or raises the existing
%      singleton*.
%
%      H = MAIN returns the handle to a new MAIN or the handle to
%      the existing singleton*.
%
%      MAIN('CALLBACK',hObject,eventData,handles,...) calls the local
%      function named CALLBACK in MAIN.M with the given input arguments.
%
%      MAIN('Property','Value',...) creates a new MAIN or raises the
%      existing singleton*.  Starting from the left, property value pairs are
%      applied to the GUI before main_OpeningFcn gets called.  An
%      unrecognized property name or invalid value makes property application
%      stop.  All inputs are passed to main_OpeningFcn via varargin.
%
%      *See GUI Options on GUIDE's Tools menu.  Choose "GUI allows only one
%      instance to run (singleton)".
%
% See also: GUIDE, GUIDATA, GUIHANDLES

% Edit the above text to modify the response to help main

% Last Modified by GUIDE v2.5 17-Jan-2022 10:47:23

% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name',       mfilename, ...
                   'gui_Singleton',  gui_Singleton, ...
                   'gui_OpeningFcn', @main_OpeningFcn, ...
                   'gui_OutputFcn',  @main_OutputFcn, ...
                   'gui_LayoutFcn',  [] , ...
                   'gui_Callback',   []);
if nargin && ischar(varargin{1})
    gui_State.gui_Callback = str2func(varargin{1});
end

if nargout
    [varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
    gui_mainfcn(gui_State, varargin{:});
end
% End initialization code - DO NOT EDIT


% --- Executes just before main is made visible.
function main_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject    handle to figure
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
% varargin   command line arguments to main (see VARARGIN)

% Choose default command line output for main
handles.output = hObject;

% Update handles structure
guidata(hObject, handles);

% UIWAIT makes main wait for user response (see UIRESUME)
% uiwait(handles.figure1);


% --- Outputs from this function are returned to the command line.
function varargout = main_OutputFcn(hObject, eventdata, handles) 
% varargout  cell array for returning output args (see VARARGOUT);
% hObject    handle to figure
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)

% Get default command line output from handles structure
varargout{1} = handles.output;


% --- Executes on button press in pushbutton1.
function pushbutton1_Callback(hObject, eventdata, handles)
% hObject    handle to pushbutton1 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
global I I1
[filename,pathname] = uigetfile({'*.png';'*.jpg';'*.bmp'},'Select Picture');
str = [pathname,filename];
I1 = imread(str);
if (strcmpi(filename,'lena_gaussian.png')==1||strcmpi(filename,'lena_salt-pepper.png')==1||strcmpi(filename,'lena_speckle.png')==1)
    I=imread('lena.png');
elseif (strcmpi(filename,'barbara_gaussian.png')==1||strcmpi(filename,'barbara_salt-pepper.png')==1||strcmpi(filename,'barbara_speckle.png')==1)
    I=imread('barbara.png');
elseif (strcmpi(filename,'peppers256_gaussian.png')==1||strcmpi(filename,'peppers256_salt-pepper.png')==1||strcmpi(filename,'peppers256_speckle.png')==1)
    I=imread('peppers256.png');
else
        msgbox('Please enter the specified noise image','confirm','error');
end
axes(handles.axes1),imshow(I),title('Original drawing');
PSNR1=psnr(I1,I);
t1 = sprintf('%s%f%s','Noisy image,PSNR=',PSNR1, 'dB');
axes(handles.axes2),imshow(I1),title(t1);

% --- Executes on button press in pushbutton2.
function pushbutton2_Callback(hObject, eventdata, handles)
% hObject    handle to pushbutton2 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
global I I1
I2=average_filtering(I1); 
I3=median_filtering(I1); 
I4=gaussian_lowpass_filtering(I1); 
I5=butterworth_lowpass_filtering(I1); 
I6=PCA_filtering(I1); 
I7=wavelet_transform_filtering(I1); 
I8=wiener_filtering(I1); 

PSNR2=psnr(I2,I);
t2 = sprintf('%s%f%s','Mean filtered image,PSNR=',PSNR2, 'dB');
axes(handles.axes3),imshow(I2),title(t2);
PSNR3=psnr(I3,I);
t3 = sprintf('%s%f%s','Median filtered image,PSNR=',PSNR3, 'dB');
axes(handles.axes4),imshow(I3),title(t3);
PSNR4=psnr(I4,I);
t4 = sprintf('%s%f%s','Gaussian low pass filtered image,PSNR=',PSNR4, 'dB');
axes(handles.axes5),imshow(I4),title(t4);
PSNR5=psnr(I5,I);
t5 = sprintf('%s%f%s','Butterworth filtered image,PSNR=',PSNR5, 'dB');
axes(handles.axes6),imshow(I5),title(t5);
PSNR6=psnr(I6,I);
t6 = sprintf('%s%f%s','PCA Filtered image,PSNR=',PSNR6, 'dB');
axes(handles.axes7),imshow(I6),title(t6);
PSNR7=psnr(I7,I);
t7 = sprintf('%s%f%s','Image after wavelet transform,PSNR=',PSNR7, 'dB');
axes(handles.axes8),imshow(I7),title(t7);
PSNR8=psnr(I8,I);
t8 = sprintf('%s%f%s','Wiener filtered image,PSNR=',PSNR8, 'dB');
axes(handles.axes9),imshow(I8),title(t8);

        

4, Operation results

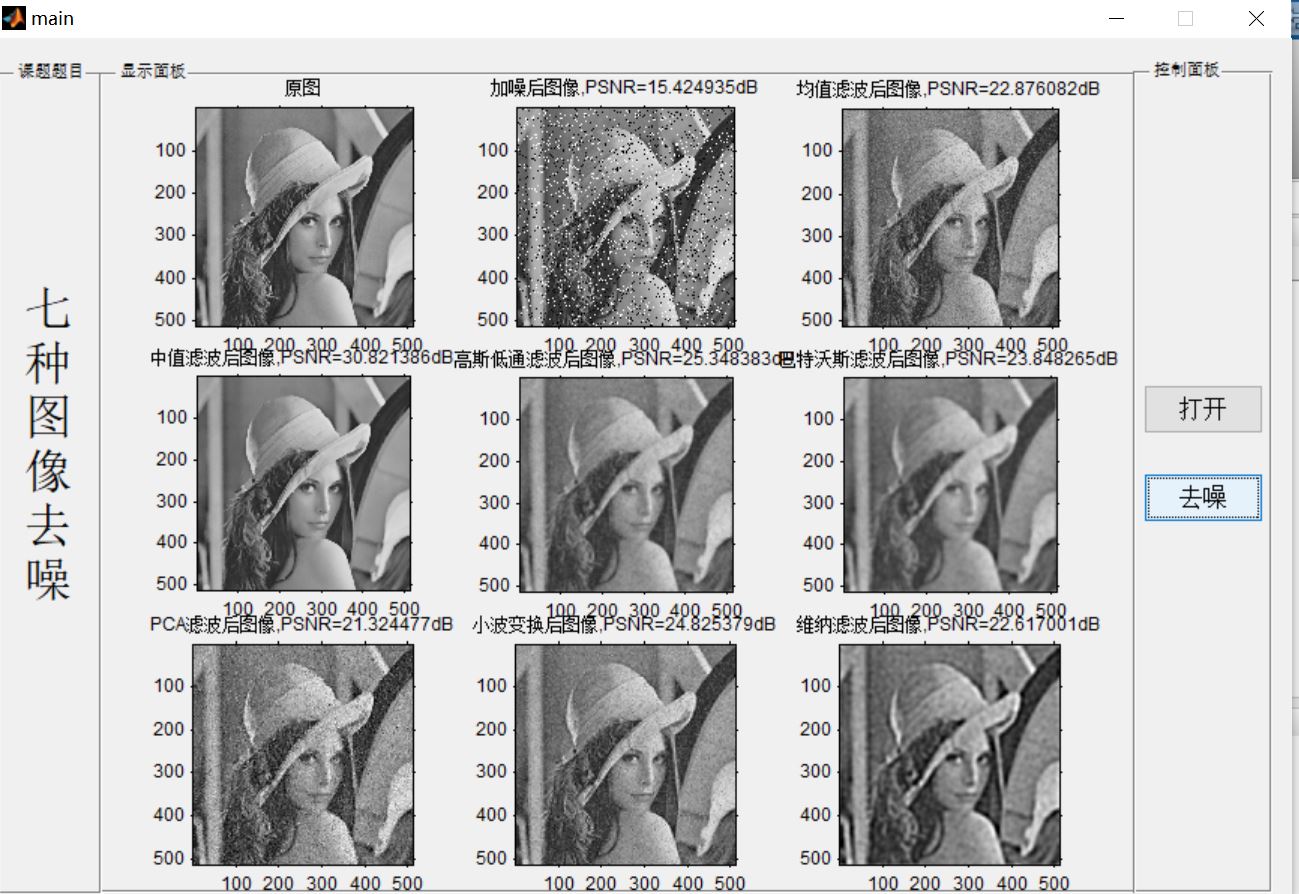
5, matlab version and references

1 matlab version
2014a

2 references
[1] Cai Limei MATLAB image processing -- theory, algorithm and example analysis [M] Tsinghua University Press, 2020
[2] Yang Dan, Zhao Haibin, long Zhe Detailed explanation of MATLAB image processing example [M] Tsinghua University Press, 2013
[3] Zhou pin MATLAB image processing and graphical user interface design [M] Tsinghua University Press, 2013
[4] Liu Chenglong Proficient in MATLAB image processing [M] Tsinghua University Press, 2015
[5]Implementation principle of traditional image denoising algorithm based on matlab