1, Introduction
Particle swarm optimization (PSO) is a numerical optimization algorithm based on swarm intelligence. It was proposed by social psychologist James Kennedy and electrical engineer Russell Eberhart in 1995. Since the birth of PSO, it has been improved in many aspects. This part will introduce the basic principle and process of particle swarm optimization algorithm.
1.1 particle swarm optimization
Particle swarm optimization (PSO) is a population intelligent algorithm, which is inspired by the learning of birds or fish swarm. It is used to solve nonlinear, nonconvex or combinatorial optimization problems in many scientific and engineering fields.

1.1.1 algorithm idea
Many birds are social and form different groups for various reasons. Birds may be of different sizes, appear in different seasons, and may even be composed of different species that can cooperate well in the group. More eyes and ears mean more opportunities to find food and predators in time. Birds are always good for the survival of their members in many ways:
Foraging: sociobiologist E.O.Wilson says that, at least in theory, individual members of a group can benefit from the discoveries and previous experience of other members in the search for food [1]. If the food source of a flock of birds is the same, some species of birds will gather together in a non competitive way. In this way, more birds can take advantage of other birds' discovery of food location.
Resist predators: birds have many advantages in protecting themselves from predators.
More ears and eyes mean more opportunities to detect predators or any other potential hazards;
A flock of birds may confuse or suppress predators through siege or agile flight;
In groups, mutual warning can reduce the risk of any bird.
Aerodynamics: when birds fly in groups, they often arrange themselves into specific shapes or formations. The number of birds in the flock is different, and each bird produces different airflow when stirring its wings, which will lead to different wind patterns. These formations will make full use of different types, so that birds in flight can use the surrounding air in the most energy-saving way.
The development of particle swarm optimization algorithm needs to simulate some advantages of bird swarm. However, in order to understand an important property of swarm intelligence and particle swarm optimization, it is worth mentioning some disadvantages of bird swarm. When birds flock, they also pose some risks. More ears and eyes mean more wings and mouth, which leads to more noise and movement. In this case, more predators can locate the birds and pose a continuous threat to the birds. A larger group will also need more food, which leads to more food competition, which may eliminate some weaker birds in the group. It should be pointed out here that PSO does not have the disadvantage of simulating the behavior of bird groups. Therefore, it is not allowed to kill any individual in the search process, while in genetic algorithm, some weaker individuals will die. In PSO, all individuals will survive and strive to become stronger throughout the search process. In particle swarm optimization, the improvement of potential solution is the result of cooperation, while in evolutionary algorithm, it is because of competition. This concept makes swarm intelligence different from evolutionary algorithms. In short, in evolutionary algorithms, each iteration has a new population evolution, while in swarm intelligence algorithms, each generation has individuals to make themselves better. The identity of the individual does not change with the iteration. Mataric[2] gives the following flock rules:
Safe roaming: when birds fly, there is no collision with each other or with obstacles;
Dispersion: each bird will keep a minimum distance from other birds;
Aggregation: each bird will also keep a maximum distance from other birds;
Homing: all birds are likely to find food sources or nests.
When designing particle swarm optimization algorithm, these four rules are not used to simulate the group behavior of birds. In the basic particle swarm optimization model developed by Kennedy and Eberhart, the movement of agent does not follow the rules of safe roaming and dispersion. In other words, during the movement of the basic particle swarm optimization algorithm, the agents in the particle swarm optimization algorithm are allowed to be as close to each other as possible. Aggregation and homing are effective in particle swarm optimization model. In particle swarm optimization, the agent must fly in a specific area in order to maintain the maximum distance from any other agent. This is equivalent to that in the whole process, the search always stays within or at the boundary of the search space. The fourth rule, homing, means that any agent in the group can achieve global optimization.
In the development of PSO model, Kennedy and Eberhart put forward five basic principles to judge whether a group of agents is a group:
Proximity principle: the agent group should be able to calculate simple space and time;
Quality principle: the agent group can respond to the quality factors in the environment;
Multi response principle: the agent group should not engage in activities in too narrow channels;
Stability principle: the agent group cannot change its behavior pattern every time the environment changes;
Adaptability principle: when the calculation cost is small, the agent group can change its behavior pattern.
1.1.2 particle swarm optimization process
Considering these five principles, Kennedy and Eberhart developed a PSO model for function optimization. In particle swarm optimization algorithm, random search method is adopted and swarm intelligence is used to solve it. In other words, particle swarm optimization algorithm is a population intelligent search algorithm. This search is done by a set of randomly generated possible solutions. This set of possible solutions is called a group, and each possible solution is called a particle.
In particle swarm optimization algorithm, particle search is affected by two learning methods. Each particle is learning from other particles and learning its own experience in the process of movement. Learning from others can be called social learning, while learning from one's own experience can be called cognitive learning. As a result of social learning, the particle stores the best solution accessed by all particles in the group in its memory, which is called gbest. Through cognitive learning, the particle stores in its memory the best solution it has visited so far, which is called pbest.
The change in the direction and size of any particle is determined by a factor called velocity, which is the rate of change of position relative to time. For PSO, the iteration is time. In this way, for particle swarm optimization algorithm, speed can be defined as the change rate of position relative to iteration. As the iteration counter unit increases, the dimension of velocity v is the same as position x.
For the D-dimensional search space, under the time step T, the ith particle in the population is composed of the D-dimensional vector x i t = (x I 1 T, , x I D t) t X_ I ^ t = {(x {I1} ^ t, \ cdots, X {ID} T) t} xit = (xi1t,..., xiDt) t, and its velocity is represented by another D-dimensional vector V i t = (V I 1 T, , V I D t) t v_ I ^ t = {(V {I1} ^ t, \ cdots, V {ID} T) t} vit = (vi1t,..., viDt) t indicates. The location of the optimal solution visited by the ith particle is p i t = (P I 1 T, , P I D t) t P_ I ^ t = {\ left ({P {I1} ^ t, \ cdots, P {ID} ^ t} \ right) ^ t} pit = (pi1t,..., piDt) t indicates that the index of the optimal particle in the population is "g". The velocity and position of the ith particle are updated respectively by the following formula:
v i d t + 1 = v i d t + c 1 r 1 ( p i d t − x i d t ) + c 2 r 2 ( p g d t − x i d t ) (1) v_{id}^{t + 1} = v_{id}^t + {c_1}{r_1}\left( {p_{id}^t - x_{id}^t} \right) + {c_2}{r_2}\left( {p_{gd}^t - x_{id}^t} \right)\tag 1vidt+1=vidt+c1r1(pidt−xidt)+c2r2(pgdt−xidt)(1)
x i d t + 1 = x i d t + v i d t + 1 (2) x_{id}^{t + 1} = x_{id}^t + v_{id}^{t + 1}\tag 2xidt+1=xidt+vidt+1(2)
Where d=1,2,..., D is the dimension, i=1,2,..., s is the particle index, and S is the population size. The c2 and c2 are simply referred to as the cognitive constants, or the social scaling coefficients, respectively. r1 and r2 are random numbers satisfying uniform distribution [0,1]. The above two formulas update each dimension of each particle separately. The only connection between different dimensions in the problem space is introduced through the objective function, that is, the best positions gbest and pbest found at present [3]. The algorithm flow of PSO is as follows:
1.1.3 interpretation and update equation
The right side of the speed update equation (1) consists of three parts 3:
The velocity v of the previous time can be regarded as a momentum term, which is used to store the previous direction of motion, in order to prevent the particles from changing direction violently.
The second is the cognitive or self part. Through this item, the current position of the particle will move to its own best position, so that the particle will remember its best position throughout the search process, so as to avoid wandering around. It should be noted here that pidt xidt is a vector from xidt to pidt in one direction, so as to attract the current position to the best position of the particle. The order of the two cannot be changed, otherwise the current position will be far away from the best position.
The third is the social part, which is responsible for sharing information through groups. Through this item, the particle moves to the best individual in the group, that is, each individual learns from other individuals in the group. Similarly, both should be pgbt xidt.
It can be seen that the cognitive scale parameter c1 regulates the maximum step size of the particle in its optimal position direction, while the social scale parameter c2 regulates the maximum step size in the global optimal particle direction. Figure 2 shows the typical geometry of particles moving in two-dimensional space.
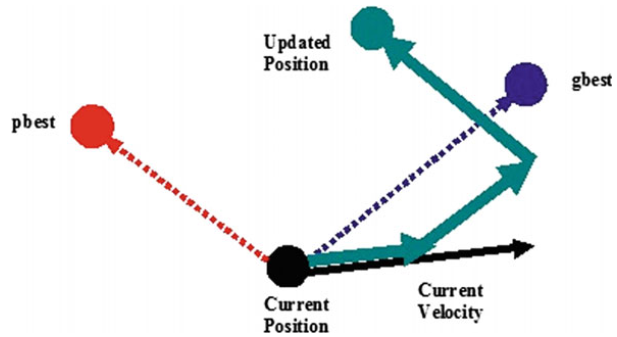
Figure 2 geometric description of particle movement in particle swarm optimization
It can be seen from the renewal equation that Kennedy and Eberhart's PSO design follows the five basic principles of PSO. In the process of particle swarm optimization, a series of time steps are calculated in d-dimensional space. At any time step, the population follows the guiding direction of gbest and pbest, that is, the population responds to quality factors and follows the quality principle. Because there are uniformly distributed random numbers r1 and r2 in the velocity renewal equation, the current position is randomly distributed between pbest and gbest, which proves the diversity of the response principle. In the process of particle swarm optimization, only when the particle swarm receives better information from gbest, the random motion will occur, which proves the stability principle of particle swarm optimization process. The population changes when gbest changes, so it follows the principle of adaptability.
1.2 parameters in particle swarm optimization
The convergence speed and optimization ability of any population-based algorithm are affected by its parameter selection. Generally, because the parameters of these algorithms are highly dependent on the problem parameters, it is impossible to give general suggestions on the parameter setting of these algorithms. However, the existing theoretical and / or experimental studies give a general range of parameter values. Similar to other population-based search algorithms, due to the random factors r1 and r2 in the search process, the parameter adjustment of general PSO has always been a challenging task. The basic version of PSO requires only a few parameters. This chapter only discusses the parameters of the basic version of PSO introduced in [4].
A basic parameter is group size, which is usually set empirically according to the number of decision variables in the problem and the complexity of the problem. Generally, 20-50 particles are recommended.
Another parameter is the scaling factors c1 and c2. As mentioned earlier, these parameters determine the step size of particles in the next iteration. That is, c1 and c2 determine the velocity of the particles. In the basic version of PSO, select c1=c2=2. In this case, the increase of particle s velocity is uncontrolled, which is conducive to faster convergence, but not conducive to better use of the search space. If we make c1 = c2 > 0, the particles will attract the average of pbest and gbest. The setting of c1 > c2 is conducive to multimodal problems, while c2 > c1 is conducive to single-mode problems. In the search process, the smaller the values of c1 and c2, the smoother the particle trajectory, while the larger the values of c1 and c2, the more intense the particle motion and the greater the acceleration. Researchers also proposed adaptive acceleration coefficient [5].
The stopping criterion is not only the parameter of particle swarm optimization algorithm, but also the parameter of any population-based meta heuristic algorithm. Commonly used stopping criteria are usually based on the maximum number of function evaluations or iterations, which is directly proportional to the time spent by the algorithm. A more effective stopping criterion is based on the search ability of the algorithm. If an algorithm does not significantly improve the solution within a certain number of iterations, the search should be stopped.
2, Source code
clc;
clear;
m=5;%Number of workpieces
n=4;%Number of processes
inn=50; %Population size
gnmax=50;%Number of iterations
Vmax = 5;%Maximum speed
Vmin =-5; %Minimum speed
ws=1.2;%Initial weight
we=0.4;%Inertia weight when iterating to the maximum number of times
c1 = 2.05; %c1,c2 It represents the weight of the random acceleration term that pulls the particle to the individual extreme value and the group extreme value, indicating the individual's "cognitive ability" and the group's "social guidance" function respectively
c2 = 2.05; %It is generally set to the same value, and the most common is 2.0,Another common value is 1.49445,It can ensure PSO The algorithm is convergent, but it is easy to fall into local optimization when dealing with multimodal problems
c3 = 0.5; %Innovation factor coefficient
pcmax=1;%Maximum crossover probability
pcmin=0.5;%Minimum crossover probability
pmmax=0.1;%Maximum variation probability
pmmin=0.01;%Minimum variation probability
V=zeros(inn,m*n);
for i= 1:inn
V(i,:)=4*rand(1,m*n)-2; %Initialization speed(-2,2)
end
[chromosome,chromosomea,chromosomeb]=initialization(m,n,inn);%Generate initial population
gachromosomea=chromosomea;%Initialize genetic population
gachromosomeb=chromosomeb;
[timecost,jiqixulie]=tcost(m,n);%Workpiece processing time and machine sequence((on which machine is a process of a workpiece processed)
T=0;
for i=1:m
for j=1:n
T=T+timecost(i,j);
end
end
[f,p,ps]=objf(chromosomea,m,n,jiqixulie,timecost,T);%Return cumulative probability p Fitness function f,ps Is the proportion of fitness, that is, probability
[bestfitness,bestindex] =max(f);
zbesta = chromosomea(bestindex,:); %Group extreme position(Chromosome)
zbestb = chromosomeb(bestindex,:); %Group extreme position (position weight)
gbesta = chromosomea; %Individual extreme position (chromosome)
gbestb = chromosomeb; %Individual extreme position (position weight)
fitnessgbest = f ; %Individual extreme fitness value
fitnesszbest = bestfitness; %Population extreme fitness value
newa=zeros(inn,m*n);
newb=zeros(inn,m*n);
w=zeros(1,gnmax);
V=zeros(inn,m*n);
ymax=zeros(1,gnmax);%Optimal value of each generation
ymean1=zeros(1,gnmax);
ymean2=zeros(1,gnmax);
for gn=1:gnmax
gn
value1=max(chromosomeb(:));%Find the largest element in the particle swarm
value2=min(chromosomeb(:));%Find the smallest element in particle swarm
Vmax = 0.25*(value1-value2);%The maximum speed is set to 0 of the element value range.25 times
Vmin = -0.25*(value1-value2);
%Particle position and velocity updates
for j=1:inn
w(gn)=ws-(ws-we)*(2*gn/gnmax-(gn/gnmax)^2);%Inertia factor
%w(gn)=0.91-gnmax*0.5/gn;
V(j,:)=w(gn)*V(j,:)+c1*rand*(gbestb(j,:)-chromosomeb(j,:))+c2*rand*(zbestb-chromosomeb(j,:));%Update speed
V(j,V(j,:)>Vmax)=Vmax;%Maximum speed limit
V(j,V(j,:)<Vmin)=Vmin;%Minimum speed limit
innovation=20*rand(1,m*n)+10;
chromosomeb(j,:)=chromosomeb(j,:)+0.5*V(j,:)+c3*rand*(innovation-chromosomeb(j,:));%Update particle swarm by formula
chromosomeb(j,chromosomeb(j,:)>30)=30;%Limit maximum range
chromosomeb(j,chromosomeb(j,:)<10)=10;%Limit minimum range
end
for i=1:inn%Particle update corresponds to chromosome update
r=chromosomeb(i,:);
a=[r;chromosome];
b=a';
c=sortrows(b,1);
d=c';
chromosomea(i,:)=d(2,:);
chromosomeb(i,:)=a(1,:);
end
[f,p,ps]=objf(chromosomea,m,n,jiqixulie,timecost,T);%Particle swarm return cumulative probability p Fitness function f,ps Is the proportion of fitness, that is, probability
[fit,p,ps]=objf(gachromosomea,m,n,jiqixulie,timecost,T);%Genetic return cumulative probability p Fitness function f,ps Is the proportion of fitness, that is, probability
%Individual extremum and group extremum update
for j=1:inn
%Individual extremum update
if f(j)>fitnessgbest(j)
gbesta(j,:)=chromosomea(j,:);
gbestb(j,:)=chromosomeb(j,:);
fitnessgbest(j)=f(j);
end
%Population extremum update
if f(j)>fitnesszbest
zbesta=chromosomea(j,:);
zbestb=chromosomeb(j,:);
fitnesszbest=f(j);
end
%If the particle swarm produces a better individual, replace it with the one in the corresponding heredity
if f(j)>fit(j)
gachromosomea(j,:)=chromosomea(j,:);
gachromosomeb(j,:)=chromosomeb(j,:);
end
end
% [f,p,ps]=objf(chromosomea,m,n,jiqixulie,timecost,T);%Return cumulative probability p Fitness function f,ps Is the proportion of fitness, that is, probability
% for i=1:m*n
% x(i)=sum(chromosomeb(:,i))/inn;
% end
% [best,index]=max(f);
% varbest=0;
% for i=1:m*n
% varbest=varbest+(x(i)-chromosomeb(index,i))*(x(i)-chromosomeb(index,i));
% end
% [wrost,index]=max(f);
% varwrost=0;
% for i=1:m*n
% varwrost=varwrost+(x(i)-chromosomeb(index,i))*(x(i)-chromosomeb(index,i));
% end
% fenzi=(max(varwrost,varbest))^0.5;
% fenmu=0;
% for i=1:m*n
% a=sum(chromosomeb(i,:)-x(i));
% fenmu=fenmu+a^0.5;
% end
% F=fenmu/fenzi
% total=0;%Variance of gene loci
% for i=1:m*n
% total=total+var(chromosomeb(:,i));
% end
% total
%Particle swarm variation
for i=1:inn
seln=sel1(p,inn);
a=chromosomeb(seln,:);
b=randi([1,inn],1,2);
newb(i,:)=chromosomeb(seln,:)+rand*(chromosomeb(b(1),:)-chromosomeb(b(2),:));
end
for i=1:inn%Particle swarm update
r=newb(i,:);
a=[r;chromosome];
b=a';
c=sortrows(b,1);
d=c';
newa(i,:)=d(2,:);
newb(i,:)=a(1,:);
end
[fi,p,ps]=objf(newa,m,n,jiqixulie,timecost,T);%Return cumulative probability p Fitness function f,ps Is the proportion of fitness, that is, probability
for i=1:inn
if f(i)<fi(i)%Take the value with larger fitness after variation
chromosomea(i,:)=newa(i,:);
chromosomeb(i,:)=newb(i,:);
end
if fi(i)>fitnessgbest(i)%Individual update
gbesta(i,:)=chromosomea(i,:);
gbestb(i,:)=chromosomeb(i,:);
fitnessgbest(i)=fi(i);
end
if fi(i)>fitnesszbest%Group renewal
zbesta=chromosomea(i,:);
zbestb=chromosomeb(i,:);
fitnesszbest=fi(i);
end
if fi(i)>fit(i)%Genetic renewal
gachromosomea(i,:)=chromosomea(i,:);
gachromosomeb(i,:)=chromosomeb(i,:);
end
end
function pcc=pro(pc)
test(1:100)=0;%take test(0)-test(100)Assign value to 0
l=round(100*pc);
test(1:l)=1;%test(0)-test(pc*100)Is 1, test(100*pc)-test(100)Is 0, where pc Cross probability
n=round(rand*99)+1;
pcc=test(n);
end
3, Operation results
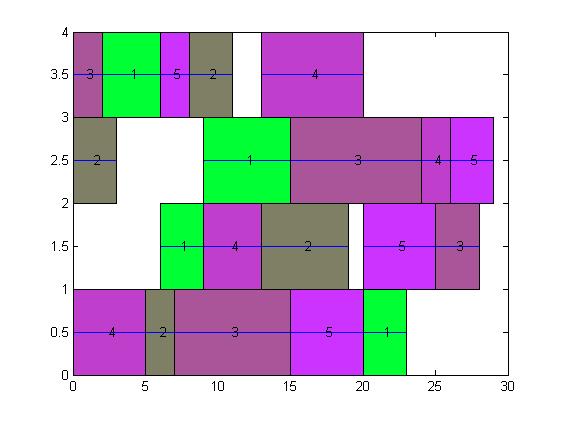
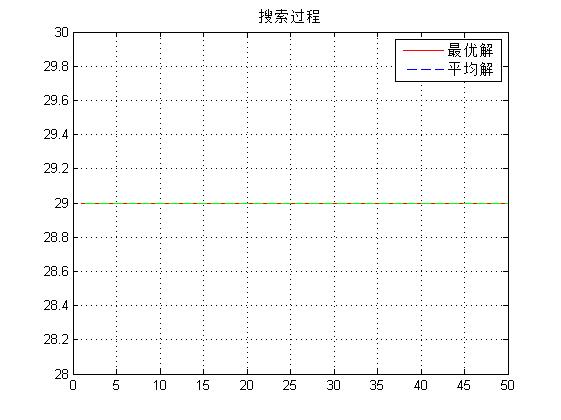
4, Remarks
Complete code or write on behalf of QQ 912100926