1, Introduction to chaotic system

0 Introduction
With the rapid development of communication technology, more and more fields need to transmit digital image signals, so the security of information transmission is becoming more and more important. Two kinds of protection technologies commonly used in digital image communication are digital watermarking technology and image encryption technology. The former protection technology is not suitable for the transmission of confidential images because it does not change the visibility of images. The latter technology changes the visibility of the image through encryption operation, so that the original image becomes indistinguishable, and the original image can only be obtained through the corresponding decryption algorithm. With the development of communication technology, image encryption technology has been more and more widely used because of its good confidentiality.
A random sequence generator is needed in the encryption algorithm. Because the discrete chaotic system is easy to implement, and the chaotic system is extremely sensitive to parameters and initial conditions, taking it as the key, the system has excellent cryptographic characteristics. At the same time, its irregularity in the two-dimensional phase plane makes it more suitable for image encryption.
According to the storage characteristics of image data, an image encryption algorithm is designed by using discrete chaotic dynamic system. All keys are generated by discrete chaotic mapping, so the algorithm does not affect the efficiency and speed of encryption / decryption due to the increase of key setting. Due to the use of chaotic mapping, it increases the difficulty of decoding and improves the security. The simulation results show that the algorithm can effectively encrypt / decrypt the number of digital images.

1 chaotic system
Chaos is a bounded internal random process with time ergodicity. This process is neither periodic nor convergent. Any two similar points will show exponential divergence after several chaotic iterations, so it is difficult to predict the initial values and parameters of chaotic system. In addition, the chaotic orbit is extremely irregular and the system output is similar to random noise. These characteristics make chaotic mapping very suitable for the design of cryptosystems.

Lyapunov exponent is an important criterion to judge the chaotic state of the system. When the Lyapunov exponent is less than zero, the motion state of the system is stable and insensitive to the initial conditions; When Lyapunov exponent is greater than zero, the system state is unstable and sensitive to initial conditions; If the Lyapunov exponent is zero, it corresponds to a critical state. Since the maximum Lyapunov exponent of the system determines the main evolution trend of the system, we can judge whether the system is in a chaotic state by whether the maximum Lyapunov exponent of the time series is greater than zero.

Taking the simple one-dimensional discrete chaotic system Logistic as an example, its dynamic system is:

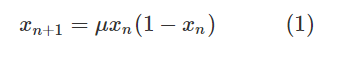
Among them, μ Is the control parameter. The chaotic state is shown in Figure 1.
As can be seen from the figure, in 3< μ< Between 3.5699456 and 3.5699456, the system is in periodic state< μ< At 4 o'clock, the system began to enter a chaotic state.
For Logistic chaotic system, a one-dimensional piecewise linear chaotic system (pwlcm) is proposed. Its dynamic equation is:

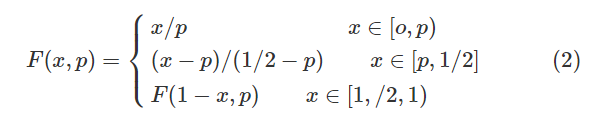
Where, x ∈ I = [0,1], P ∈ (0,1 / 2), P is the control parameter, and F is a piecewise linear chaotic map realized under the limited precision of L-bit. Its chaotic state is shown in Fig. 2.

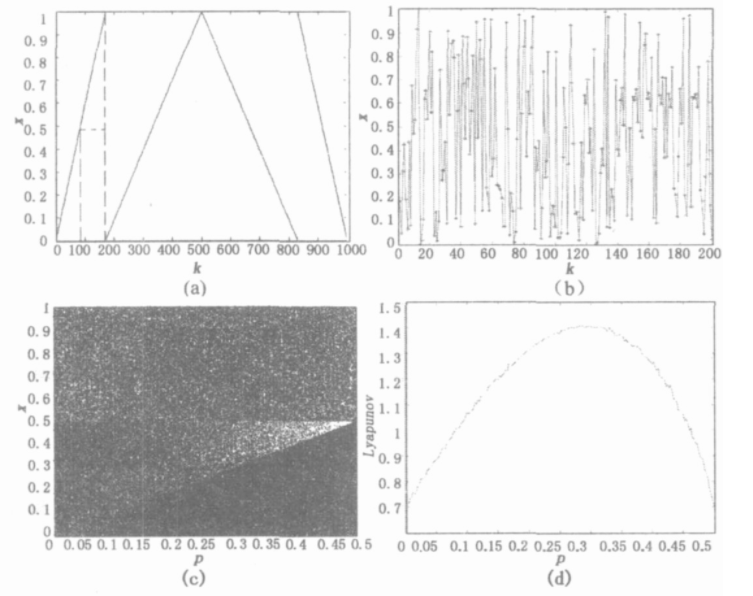
Fig. 2 Pwlcm chaotic state diagram

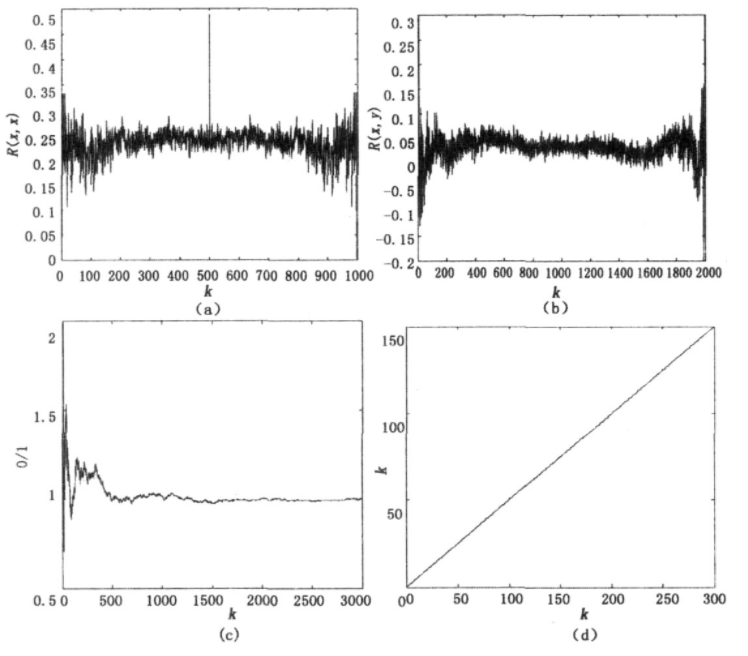
Fig. 3 Comparison of sequence quantization performance

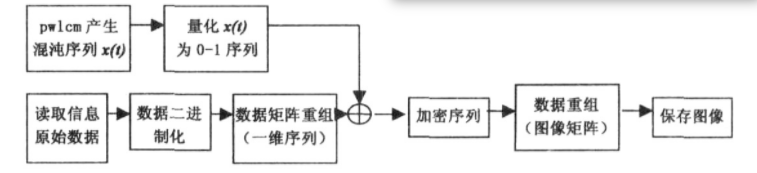
Fig. 4 flow chart of encryption algorithm
As shown in the figure, (a) represents the linear piecewise relationship of Pwlcm; (b) Is the chaotic sequence diagram, which shows that Pwlcm dynamic system is a chaotic dynamic system; © , (d) The periodic multiplication bifurcation and Lyapunov exponent spectrum are respectively. It can be seen that the Lyapunov of Pwlcm system is greater than zero in the whole value range of control parameter p, which has a larger key value space than Logistic system. At the same time, it can be seen from figure (b) that Pwlcm system has uniform invariant distribution and high ergodicity, mixing and certainty, so it can produce strong random sequences, Suitable for encryption system.

2 chaotic quantization
For Pwlcm dynamic system, sequence quantization is carried out in the following way to generate computer standard binary 0-1 sequence stream {Sm (t)}.

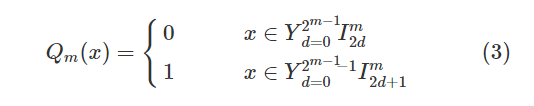
Where m > 0 is any positive integer, Im0, Im1, Im2... Are 2m consecutive bisection intervals of interval [0, 1]. Because the chaotic sequence {x (t)} has good random statistical characteristics [3,4], the generated {Sm(t)} has an equilibrium 0-1 ratio and sum in theory δ- like autocorrelation and other excellent statistical characteristics. The quantization results are shown in Figure 3.
In Figure 3,
(a) Represents the autocorrelation function of 0-1 sequence flow, which shows δ- The autocorrelation characteristic of like shows that the chaotic system is aperiodic under certain calculation accuracy.
(b) Represents the cross-correlation function of two sequence streams with initial value difference of 0.00000015. It can be seen from the figure that the quantized sequence flow has strong randomness. When the initial value difference is very small, the sequence flow is completely irrelevant, which also fully shows its initial value sensitivity.
© Represents the number ratio of 0-1 values of the quantized sequence. It can be seen that after several iterations, the ratio of the system is approximately 1, which fully shows the ergodicity of the chaotic system.
(d) Represents the linear complexity of a random sequence.

From the point of view of cryptography, the linear complexity curve of sequence is a very effective measure to characterize the unpredictability and randomness of sequence. If the linear complexity of n-bit random sequence is expected to be about n/2, it shows that its random performance is good. Here, using the B-M synthesis algorithm, assuming that the chaotic binary sequence is a standard m sequence, the order of the linear shift register with the smallest order of the sequence is calculated, which is the linear complexity of the chaotic sequence. It can be seen from the figure that the random performance of the chaotic sequence is good and can meet the requirements of system encryption.
4 image encryption

Based on the above characteristics, Pwlcm system is applied to image encryption algorithm. The image data to be encrypted is converted into binary data, and the bit by bit XOR calculation is carried out with the quantized chaotic binary sequence, so that the chaotic signal and the encrypted information signal are intertwined to mask the visibility of the information, so as to achieve the purpose of confidentiality.

The decryption process is the same. The decrypting party uses the same initial value and control parameters to generate the same chaotic sequence, XOR bit by bit with the received encrypted signal, and restore the output of the result to obtain the original information signal. The specific encryption process is shown in Figure 4.

Although Pwlcm system has its unique advantages, it can be found that it is easy to crack for the fixed control parameter P. As shown in Fig. 2 (a), for the chaotic sequence generated by formula (2), as long as any two point pairs (x (T), X (T + 1)) and (x (t ′), X (t ′ + 1)) located on the same segment are obtained, the parameter p= (x (t ′) - x (T)) / (x (t ′ + 1) -x (t+1)) can be determined.

In order to prevent the parameter p from being broken, the general way of encrypting the stream cipher one key at a time can be changed, and the method of regularly changing the control parameter p in the encryption process can be adopted to enhance the ability of anti attack.

Figure 5 encryption and decryption simulation
Here, all keys are generated by discrete chaotic mapping, and the system generates the initial value x by random function rand (). P is selected according to the quantized value of X and the value space of P. assuming that the resolution of parameter p is L = 10, the possible different values of P are p1, p2, p3,..., PN, n = 2L, and the selection order of P is in the order of quantized value of X. The simulation results of the algorithm are shown in Figure 5.

In the whole encryption process, the quantization result of the initial value is transformed according to the value range of the control parameter P, and the result is used as the value of P for the iteration of the chaotic process. This paper considers that in the process of reading the original data for binary conversion, a single value is converted to 8-bit binary characters, and the image matrix is finally changed to n × 8, so the p value is changed every n values generated by the chaotic sequence.

According to the simulation result (b), the encrypted image information has been completely disturbed to achieve the effect of confidentiality © It can be seen from the figure that the correct key can be completely reconstructed after the decryption process, and the effect is good. As can be seen from figure (d), even when the initial value is 10-17 different, the encrypted data cannot be reconstructed, which shows that it has strong anti attack ability.

2, Partial source code

function varargout = ChaosEncrypt(varargin)
% CHAOSENCRYPT MATLAB code for ChaosEncrypt.fig
%      CHAOSENCRYPT, by itself, creates a new CHAOSENCRYPT or raises the existing
%      singleton*.
%
%      H = CHAOSENCRYPT returns the handle to a new CHAOSENCRYPT or the handle to
%      the existing singleton*.
%
%      CHAOSENCRYPT('CALLBACK',hObject,eventData,handles,...) calls the local
%      function named CALLBACK in CHAOSENCRYPT.M with the given input arguments.
%
%      CHAOSENCRYPT('Property','Value',...) creates a new CHAOSENCRYPT or raises the
%      existing singleton*.  Starting from the left, property value pairs are
%      applied to the GUI before ChaosEncrypt_OpeningFcn gets called.  An
%      unrecognized property name or invalid value makes property application
%      stop.  All inputs are passed to ChaosEncrypt_OpeningFcn via varargin.
%
%      *See GUI Options on GUIDE's Tools menu.  Choose "GUI allows only one
%      instance to run (singleton)".
%
% See also: GUIDE, GUIDATA, GUIHANDLES

% Edit the above text to modify the response to help ChaosEncrypt

% Last Modified by GUIDE v2.5 25-Feb-2022 23:21:04

% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name',       mfilename, ...
                   'gui_Singleton',  gui_Singleton, ...
                   'gui_OpeningFcn', @ChaosEncrypt_OpeningFcn, ...
                   'gui_OutputFcn',  @ChaosEncrypt_OutputFcn, ...
                   'gui_LayoutFcn',  [] , ...
                   'gui_Callback',   []);
if nargin && ischar(varargin{1})
    gui_State.gui_Callback = str2func(varargin{1});
end

if nargout
    [varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
    gui_mainfcn(gui_State, varargin{:});
end
% End initialization code - DO NOT EDIT


% --- Executes just before ChaosEncrypt is made visible.
function ChaosEncrypt_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject    handle to figure
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
% varargin   command line arguments to ChaosEncrypt (see VARARGIN)

% Choose default command line output for ChaosEncrypt
handles.output = hObject;

% Update handles structure
guidata(hObject, handles);

% UIWAIT makes ChaosEncrypt wait for user response (see UIRESUME)
% uiwait(handles.figure1);


% --- Outputs from this function are returned to the command line.
function varargout = ChaosEncrypt_OutputFcn(hObject, eventdata, handles) 
% varargout  cell array for returning output args (see VARARGOUT);
% hObject    handle to figure
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)

% Get default command line output from handles structure
varargout{1} = handles.output;


% --- Executes on selection change in popupmenu5.
function popupmenu5_Callback(hObject, eventdata, handles)
% hObject    handle to popupmenu5 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)

% Hints: contents = cellstr(get(hObject,'String')) returns popupmenu5 contents as cell array
%        contents{get(hObject,'Value')} returns selected item from popupmenu5


% --- Executes during object creation, after setting all properties.
function popupmenu5_CreateFcn(hObject, eventdata, handles)
% hObject    handle to popupmenu5 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    empty - handles not created until after all CreateFcns called

% Hint: popupmenu controls usually have a white background on Windows.
%       See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
    set(hObject,'BackgroundColor','white');
end


% --- Executes on selection change in popupmenu6.
function popupmenu6_Callback(hObject, eventdata, handles)
% hObject    handle to popupmenu6 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)

% Hints: contents = cellstr(get(hObject,'String')) returns popupmenu6 contents as cell array
%        contents{get(hObject,'Value')} returns selected item from popupmenu6


% --- Executes during object creation, after setting all properties.
function popupmenu6_CreateFcn(hObject, eventdata, handles)
% hObject    handle to popupmenu6 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    empty - handles not created until after all CreateFcns called

% Hint: popupmenu controls usually have a white background on Windows.
%       See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
    set(hObject,'BackgroundColor','white');
end



function scramble_num_edit_Callback(hObject, eventdata, handles)
% hObject    handle to scramble_num_edit (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)

% Hints: get(hObject,'String') returns contents of scramble_num_edit as text
%        str2double(get(hObject,'String')) returns contents of scramble_num_edit as a double


% --- Executes during object creation, after setting all properties.
function scramble_num_edit_CreateFcn(hObject, eventdata, handles)
% hObject    handle to scramble_num_edit (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    empty - handles not created until after all CreateFcns called

% Hint: edit controls usually have a white background on Windows.
%       See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
    set(hObject,'BackgroundColor','white');
end



function Valtrans_num_edit_Callback(hObject, eventdata, handles)
% hObject    handle to Valtrans_num_edit (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)

% Hints: get(hObject,'String') returns contents of Valtrans_num_edit as text
%        str2double(get(hObject,'String')) returns contents of Valtrans_num_edit as a double


% --- Executes during object creation, after setting all properties.
function Valtrans_num_edit_CreateFcn(hObject, eventdata, handles)
% hObject    handle to Valtrans_num_edit (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    empty - handles not created until after all CreateFcns called

% Hint: edit controls usually have a white background on Windows.
%       See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
    set(hObject,'BackgroundColor','white');
end



function SecretKey_edit_Callback(hObject, eventdata, handles)
% hObject    handle to SecretKey_edit (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)

% Hints: get(hObject,'String') returns contents of SecretKey_edit as text
%        str2double(get(hObject,'String')) returns contents of SecretKey_edit as a double


% --- Executes during object creation, after setting all properties.
function SecretKey_edit_CreateFcn(hObject, eventdata, handles)
% hObject    handle to SecretKey_edit (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    empty - handles not created until after all CreateFcns called

% Hint: edit controls usually have a white background on Windows.
%       See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
    set(hObject,'BackgroundColor','white');
end

3, Operation results

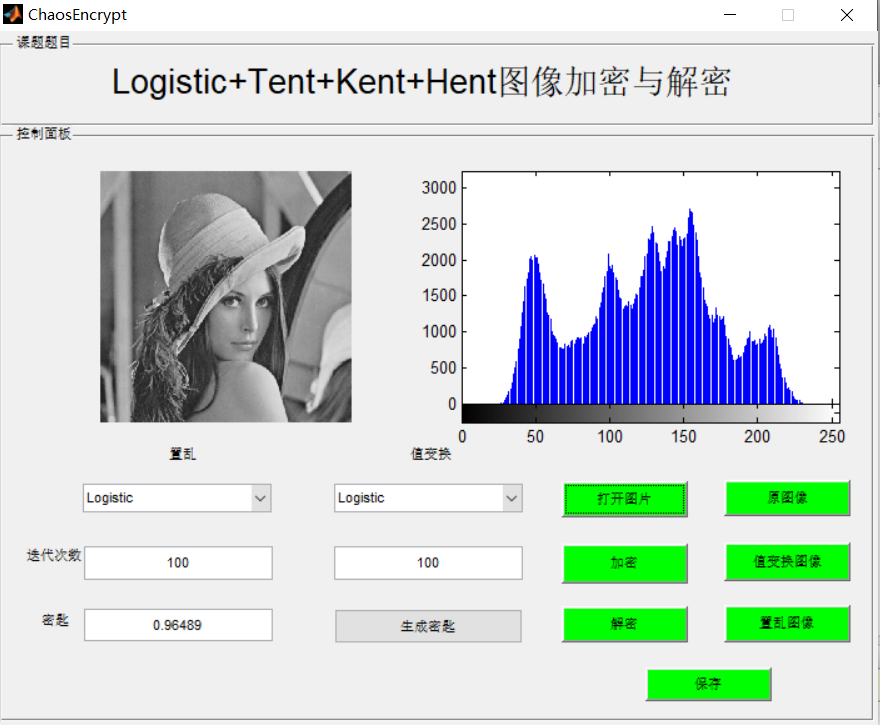
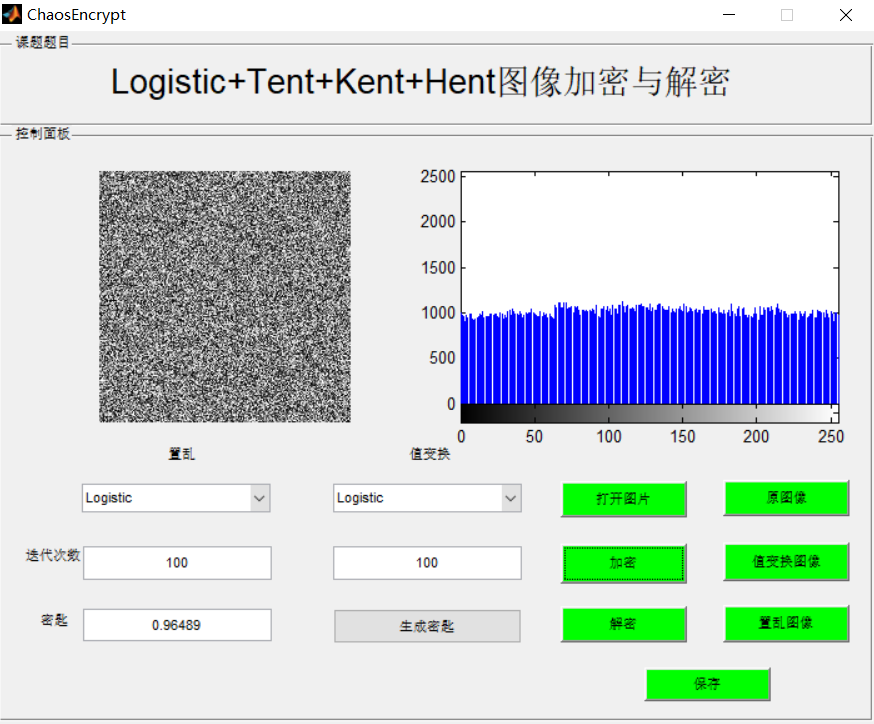
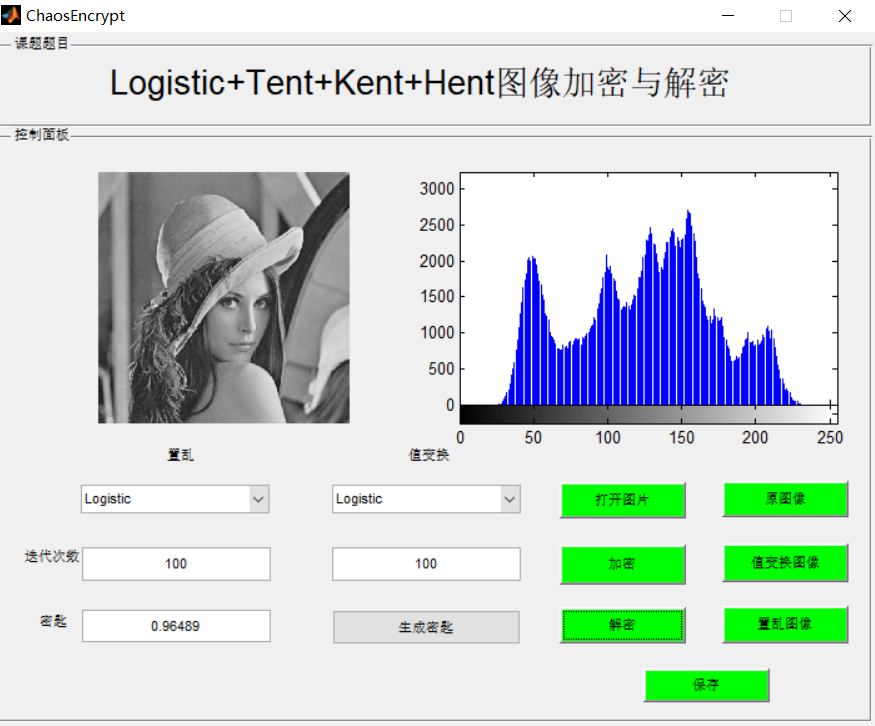
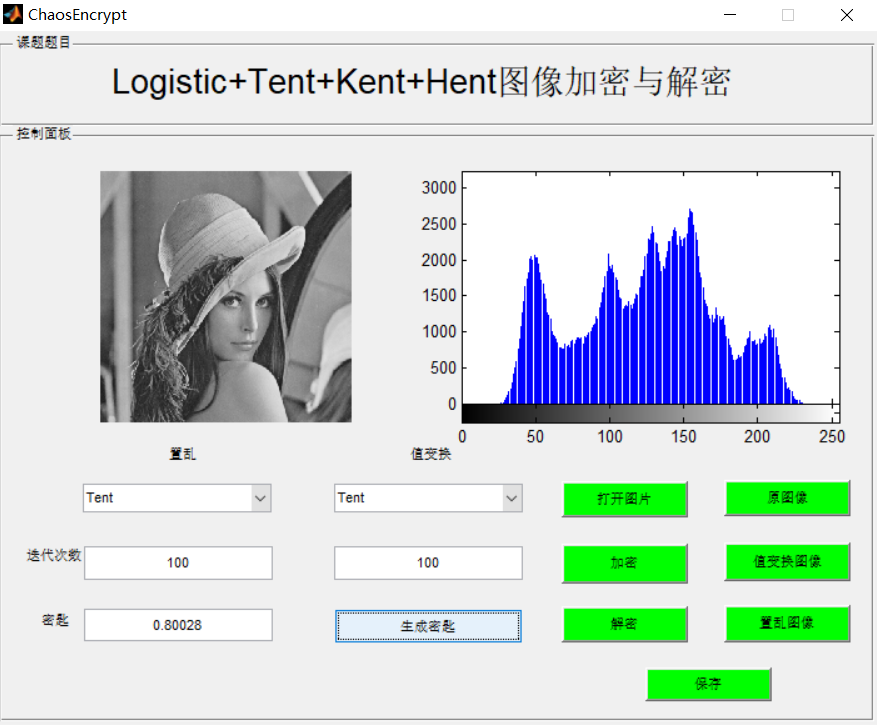
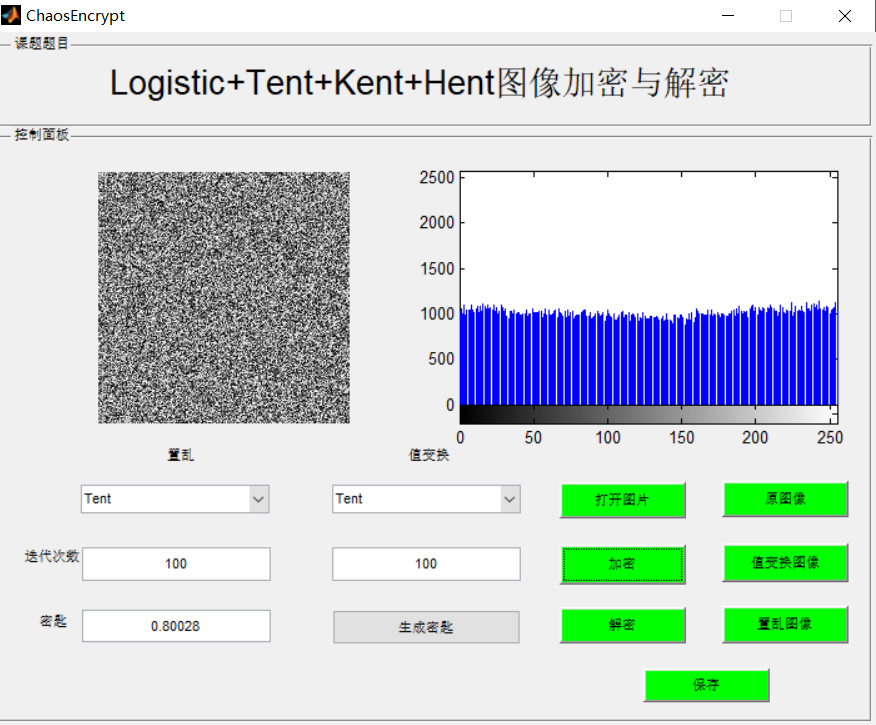
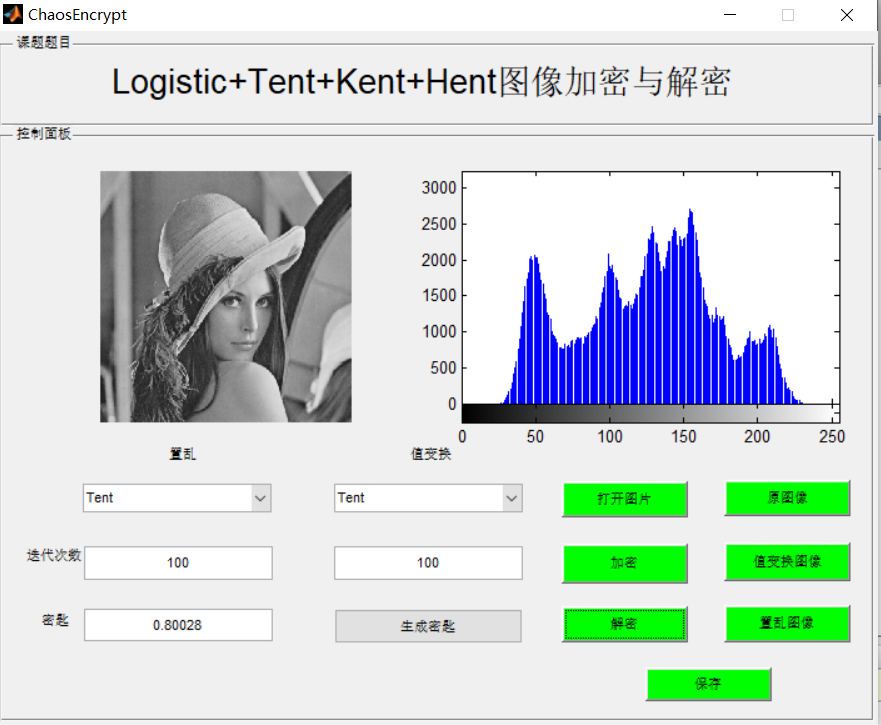
4, matlab version and references

1 matlab version
2014a

2 references
[1] Cai Limei MATLAB image processing -- theory, algorithm and example analysis [M] Tsinghua University Press, 2020
[2] Yang Dan, Zhao Haibin, long Zhe Detailed explanation of MATLAB image processing example [M] Tsinghua University Press, 2013
[3] Zhou pin MATLAB image processing and graphical user interface design [M] Tsinghua University Press, 2013
[4] Liu Chenglong Proficient in MATLAB image processing [M] Tsinghua University Press, 2015