1, Purpose of the experiment:
- 1) Be familiar with and master the principle and implementation process of five basic two-dimensional geometric transformations, including translation, proportion, symmetry, rotation and staggered cutting;
- 2) Be familiar with and master the principle and implementation process of two-dimensional coincidence transformation;
- 3) Master the methods of translation, rotation, scaling and staggered transformation in OpenGL program;
- 4) Be able to design the geometric transformation program according to the learning tutorial to realize the specific geometric transformation.
2, Experimental content
There are six questions, of which the sixth is a bonus question. Please realize the demonstration of the sample according to the given experimental results and the reference programming program
Show the effect, copy the program code and experimental screenshot to the experimental report.
Topic 1:
Design program to realize translation transformation.
- Draw the first square (2 * 2 size) at the center of the window;
- Translate the square right by 2 units and up by 3 units to draw the second square;
- Shift the first square to the right by 2 units to draw the third square;
effect:

code:
#include <GL/glut.h>
void init (void)
{
glClearColor (1.0, 1.0, 1.0, 0.0);
glMatrixMode (GL_PROJECTION);
gluOrtho2D (-5.0, 5.0, -5.0, 5.0); //Set the display range to be X:-5.0~5.0, Y:-5.0~5.0
glMatrixMode (GL_MODELVIEW);
}
void drawSquare(void) //Draw a square with a center at the origin and a side length of 2
{
glBegin (GL_POLYGON); //Vertex assignments need to be counterclockwise
glVertex2f (-1.0f,-1.0f);//Lower left point
glVertex2f (1.0f,-1.0f);//Lower right point
glVertex2f (1.0f, 1.0f);//Upper right point
glVertex2f (-1.0f,1.0f);//Upper left point
glEnd ( );
}
void myDraw (void)
{
glClear (GL_COLOR_BUFFER_BIT); //empty
glLoadIdentity(); //Sets the current matrix as the identity matrix
glPushMatrix();
glColor3f (1.0, 0.0, 0.0);
drawSquare();//Middle red rectangle
glPopMatrix();
glPushMatrix();
glTranslatef(2.0f,3.0f,0.0f);
glColor3f (0.0, 1.0, 0.0);
drawSquare(); //Green rectangle above
glPopMatrix();
glPushMatrix();
glTranslatef(2.0,0.0,0.0);
glColor3f (0.0, 0.0, 1.0);
drawSquare();//Right blue rectangle
glFlush ( );
}
void main (int argc, char** argv){
glutInit (&argc, argv);
glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB);
glutInitWindowPosition (0, 0);
glutInitWindowSize (600, 600);
glutCreateWindow ("Example of geometric transformation function synthesis");
init();
glutDisplayFunc (myDraw);
glutMainLoop ( );
}
Topic 2:
Design program to realize rotation transformation.
- Draw the first square (2 * 2 size) at the center of the window;
- Translate the square 2 units to the right, 3 units up, and rotate it 30 degrees clockwise
Degrees, draw the second square; - Translate the first square 2 units to the left, 3 units to the down, and rotate 30 degrees counterclockwise to draw the third square;
effect:

code:
#include <GL/glut.h>
void init (void){
glClearColor (1.0, 1.0, 1.0, 0.0);
glMatrixMode (GL_PROJECTION);
gluOrtho2D (-5.0, 5.0, -5.0, 5.0); //Set the display range to be X:-5.0~5.0, Y:-5.0~5.0
glMatrixMode (GL_MODELVIEW);
}
void drawSquare(void) //Draw a square with a center at the origin and a side length of 2
{
glBegin (GL_POLYGON); //Vertex assignments need to be counterclockwise
glVertex2f (-1.0f,-1.0f);//Lower left point
glVertex2f (1.0f,-1.0f);//Lower right point
glVertex2f (1.0f, 1.0f);//Upper right point
glVertex2f (-1.0f,1.0f);//Upper left point
glEnd ( );
}
void myDraw (void){
glClear (GL_COLOR_BUFFER_BIT); //empty
glLoadIdentity(); //Sets the current matrix as the identity matrix
glPushMatrix();
glColor3f (1.0, 0.0, 0.0);
drawSquare();//Middle red rectangle
glPopMatrix();
glPushMatrix();
glTranslatef(2.0f,3.0f,0.0f);
glRotatef(-30.0,0.0,0.0,1.0);
glColor3f (0.0, 1.0, 0.0);
drawSquare(); //Green rectangle above
glPopMatrix();
glPushMatrix();
glTranslatef(-2.0,-3.0,0.0);
glRotatef(30.0,0.0,0.0,1.0);
glColor3f (0.0, 0.0, 1.0);
drawSquare();//Right blue rectangle
glFlush ( );
}
void main (int argc, char** argv){
glutInit (&argc, argv);
glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB);
glutInitWindowPosition (0, 0);
glutInitWindowSize (600, 600);
glutCreateWindow ("Example of geometric transformation function synthesis");
init();
glutDisplayFunc (myDraw);
glutMainLoop ( );
}
Topic 3:
Design program to realize scale transformation.
-
Draw the first square (2 * 2 size) at the center of the window;
-
Translate the square 2 units to the right and 3 units up, keep the X and Z directions unchanged, enlarge the Y direction to 1.5 times the original, and draw the second square;
-
Translate the first square 2 units to the left and 3 units to the down, keep the Z direction unchanged, reduce the X direction to 0.5 times the original, and enlarge the Y direction to 1.5 times the original, and draw the third square;
effect:

code:
#include <GL/glut.h>
void init (void){
glClearColor (1.0, 1.0, 1.0, 0.0);
glMatrixMode (GL_PROJECTION);
gluOrtho2D (-5.0, 5.0, -5.0, 5.0); //Set the display range to be X:-5.0~5.0, Y:-5.0~5.0
glMatrixMode (GL_MODELVIEW);
}
void drawSquare(void) //Draw a square with a center at the origin and a side length of 2
{
glBegin (GL_POLYGON); //Vertex assignments need to be counterclockwise
glVertex2f (-1.0f,-1.0f);//Lower left point
glVertex2f (1.0f,-1.0f);//Lower right point
glVertex2f (1.0f, 1.0f);//Upper right point
glVertex2f (-1.0f,1.0f);//Upper left point
glEnd ( );
}
void myDraw (void){
glClear (GL_COLOR_BUFFER_BIT); //empty
glLoadIdentity(); //Sets the current matrix as the identity matrix
glPushMatrix();
glColor3f (1.0, 0.0, 0.0);
drawSquare();//Middle red rectangle
glPopMatrix();
glPushMatrix();
glTranslatef(2.0f,3.0f,0.0f);
glScalef(1.0,1.5,1.0);
glColor3f (0.0, 1.0, 0.0);
drawSquare(); //Green rectangle above
glPopMatrix();
glPushMatrix();
glTranslatef(-2.0,-3.0,0.0);
glScalef(0.5,1.5,1.0);
glColor3f (0.0, 0.0, 1.0);
drawSquare();//Right blue rectangle
glFlush ( );
}
void main (int argc, char** argv){
glutInit (&argc, argv);
glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB);
glutInitWindowPosition (0, 0);
glutInitWindowSize (600, 600);
glutCreateWindow ("Example of geometric transformation function synthesis");
init();
glutDisplayFunc (myDraw);
glutMainLoop ( );
}
Topic 4:
Using rotation transformation, the program is designed to realize three diamond displays. The radius of the short axis of the diamond is set to 1 and the radius of the long axis is set to 2. (Note: different transformation patterns will be obtained if the transformation order is different)
effect:
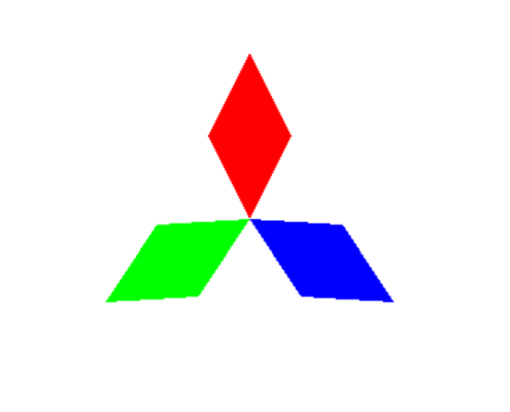
code:
#include <GL/glut.h>
void init (void){
glClearColor (1.0, 1.0, 1.0, 0.0);
glMatrixMode (GL_PROJECTION);
gluOrtho2D (-5.0, 5.0, -5.0, 5.0); //Set the display range to be X:-5.0~5.0, Y:-5.0~5.0
glMatrixMode (GL_MODELVIEW);
}
void drawSquare(void) //Draw a square with a center at the origin and a side length of 2
{
glBegin (GL_POLYGON); //Vertex assignments need to be counterclockwise
glVertex2f (0.0f,2.0f);
glVertex2f (0.5f,1.0f);
glVertex2f (0.0f,0.0f);//The major axis radius is set to 2
glVertex2f (-0.5f,1.0f);//The minor axis radius is set to 1
glVertex2f (0.0f,2.0f);
glEnd ( );
}
void myDraw (void){
glClear (GL_COLOR_BUFFER_BIT); //empty
glLoadIdentity(); //Sets the current matrix as the identity matrix
glPushMatrix();
glColor3f (1.0, 0.0, 0.0);
drawSquare();//Middle red rectangle
glPopMatrix();
glPushMatrix();
glRotatef(120.0,0.0,0.0,1.0);
glPushMatrix();
glColor3f (0.0, 1.0, 0.0);
drawSquare(); //Left green rectangle
glPopMatrix();
glRotatef(120.0,0.0,0.0,1.0);
glColor3f (0.0, 0.0, 1.0);
drawSquare();//Right blue rectangle
glFlush ( );
}
void main (int argc, char** argv){
glutInit (&argc, argv);
glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB);
glutInitWindowPosition (0, 0);
glutInitWindowSize (600, 600);
glutCreateWindow ("Rhombic compound transformation");
init();
glutDisplayFunc (myDraw);
glutMainLoop ( );
}
Topic 5:
Painted head monster (the size of each rectangle is 2 * 2)
be careful:
- The sharp mouth is obtained by scaling and translating the rectangle, not drawing a diamond.
- Pendant can add a little step-by-step amplification effect.
effect:
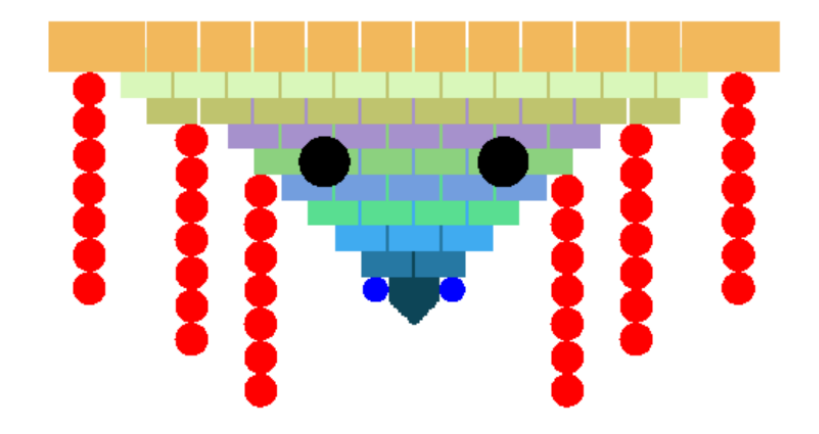
code:
#include <GL/glut.h>
#include <math.h>
float R1 = 1;
float R2 = 0.65;
float R3 = 0.5;
int i;
int j;
void init (void)
{
glClearColor (1.0, 1.0, 1.0, 0.0);
glMatrixMode (GL_PROJECTION);
gluOrtho2D (-18.0, 18.0, -18.0, 18.0); //Set the display range to be X:-5.0~5.0, Y:-5.0~5.0
glMatrixMode (GL_MODELVIEW);
}
void drawSquare(void) //Draw a square with a center at the origin and a side length of 2
{
glBegin (GL_POLYGON); //Vertex assignments need to be counterclockwise
glVertex2f (-1.0f,-1.0f);//Lower left point
glVertex2f (1.0f,-1.0f);//Lower right point
glVertex2f (1.0f, 1.0f);//Upper right point
glVertex2f (-1.0f,1.0f);//Upper left point
glEnd ( );
}
void drawCicle1(float R1 ){
int n=3600;
float PI=3.1415926f; //Define π
glBegin(GL_POLYGON);//Define drawing mode
for (i=1;i<n;i++){
glVertex2f(R1*cos(2*PI*i/n)+2.5,R1*sin(2*PI*i/n)-2.5); //Set point coordinates, a total of 3600 points, used to draw convex polygons
}
glEnd();
glBegin(GL_POLYGON);
for (i = 1; i < n; i++){
glVertex2f(R1*cos(2*PI*i/n)-4.5,R1*sin(2*PI*i/n)-2.5); //Set point coordinates, a total of 3600 points, used to draw convex polygons
}
glEnd();
}
void drawCicle2(float R2 ){
int n=3600;
float PI=3.1415926f; //Define π
for(j = 0;j<7;j++){
glBegin(GL_POLYGON);//Define drawing mode
for (i = 1; i < n; i++){
glVertex2f(R2*cos(2*PI*i/n)-7,R2*sin(2*PI*i/n)-3.65-j*1.3); //Set point coordinates, a total of 3600 points, used to draw convex polygons
}
glEnd();
}
for(j = 0;j<7;j++){
glBegin(GL_POLYGON);//Define drawing mode
for (i = 1; i < n; i++){
glVertex2f(R2*cos(2*PI*i/n)+5,R2*sin(2*PI*i/n)-3.65-j*1.3); //Set point coordinates, a total of 3600 points, used to draw convex polygons
}
glEnd();
}
for(j = 0;j<7;j++){
glBegin(GL_POLYGON);//Define drawing mode
for (i = 1; i < n; i++){
glVertex2f(R2*cos(2*PI*i/n)-9.7,R2*sin(2*PI*i/n)-1.65-j*1.3); //Set point coordinates, a total of 3600 points, used to draw convex polygons
}
glEnd();
}
for(j = 0;j<7;j++){
glBegin(GL_POLYGON);//Define drawing mode
for (i = 1; i < n; i++){
glVertex2f(R2*cos(2*PI*i/n)+7.7,R2*sin(2*PI*i/n)-1.65-j*1.3); //Set point coordinates, a total of 3600 points, used to draw convex polygons
}
glEnd();
}
for(j = 0;j<7;j++){
glBegin(GL_POLYGON);//Define drawing mode
for (i = 1; i < n; i++){
glVertex2f(R2*cos(2*PI*i/n)-13.7,R2*sin(2*PI*i/n)+0.35-j*1.3); //Set point coordinates, a total of 3600 points, used to draw convex polygons
}
glEnd();
}
for(j = 0;j<7;j++){
glBegin(GL_POLYGON);//Define drawing mode
for (i = 1; i < n; i++){
glVertex2f(R2*cos(2*PI*i/n)+11.7,R2*sin(2*PI*i/n)+0.35-j*1.3); //Set point coordinates, a total of 3600 points, used to draw convex polygons
}
glEnd();
}
}
void drawCicle3(float R3 ){
int n=3600;
float PI=3.1415926f; //Define π
glBegin(GL_POLYGON);//Define drawing mode
for (i = 1; i < n; i++){
glVertex2f(R3*cos(2*PI*i/n)-2.5,R3*sin(2*PI*i/n)-7.5); //Set point coordinates, a total of 3600 points, used to draw convex polygons
}
glEnd();
glBegin(GL_POLYGON);
for (i = 1; i < n; i++){
glVertex2f(R3*cos(2*PI*i/n)+0.5,R3*sin(2*PI*i/n)-7.5); //Set point coordinates, a total of 3600 points, used to draw convex polygons
}
glEnd();
}
void myDraw (void)//Draw a rectangle first and then a circle
{
int i, j;
float r = 0.05;
float g = 0.27;
float b = 0.34;
int x = -1, y = -7;
glClear(GL_COLOR_BUFFER_BIT); //empty
glLoadIdentity(); //Sets the current matrix as the identity matrix
//Middle rectangle
glPushMatrix();
glColor3f(1.0, 1.0, 0.0);
drawSquare(); //Yellow rectangle
glPopMatrix();
//Triangular mouth
for (i = 1; i < 10; i++) {
glPushMatrix();
glTranslatef(-1 + i * 0.0025, -7 - i * 0.2, 0.0);
glColor3f(r, g, b);
glScalef(1 - 0.1 * i, 1 - 0.1 * i, 1);
drawSquare();
glPopMatrix();
}
//face
for (i = 0; i < 10; i++) {
for (j = -i; j <= i; j += 2) {
glPushMatrix();
glTranslatef(x + j + 0.05 * j, y + i, 0.0);
glColor3f(r, g, b);
drawSquare();
glPopMatrix();
}
if(i==7){
glPushMatrix();
glTranslatef(-10 - 0.3-0.15, y + i, 0.0);
glColor3f(r, g, b);
drawSquare();
glPopMatrix();
glPushMatrix();
glTranslatef(8 + 0.3+0.15, y + i, 0.0);
glColor3f(r, g, b);
drawSquare();
glPopMatrix();
}
if(i == 8){
glPushMatrix();
glTranslatef(-11-0.5, y + i, 0.0);
glColor3f(r, g, b);
drawSquare();
glPopMatrix();
glPushMatrix();
glTranslatef(9 +0.5, y + i, 0.0);
glColor3f(r, g, b);
drawSquare();
glPopMatrix();
}
if (i == 9) {
glPushMatrix();
glTranslatef(-12-0.5, y + i, 0.0);
glColor3f(r, g, b);
drawSquare();
glPopMatrix();
glPushMatrix();
glTranslatef(10 +0.5, y + i, 0.0);
glColor3f(r, g, b);
drawSquare();
glPopMatrix();
glPushMatrix();
glTranslatef(-14 - 0.3, y + i, 0.0);
glColor3f(r, g, b);
drawSquare();
glPopMatrix();
glPushMatrix();
glTranslatef(12 + 0.3, y + i, 0.0);
glColor3f(r, g, b);
drawSquare();
glPopMatrix();
}
r += 0.1;
g += 0.2;
b += 0.3;
if (r > 1.0)
r -= 0.23f;
if (g > 1.0)
g -= 0.45f;
if (b > 1.0)
b -= 0.67f;
}
//eye
glColor4f(0, 0, 0, 0); //define color
glBegin(GL_POLYGON);//Define drawing mode
drawCicle1(R1);
//Beard
glColor4f(1, 0, 0, 0); //define color
glBegin(GL_POLYGON);//Define drawing mode
drawCicle2(R2);
glFlush ( );
//nose
glColor4f(0, 0, 1, 0); //define color
glBegin(GL_POLYGON);//Define drawing mode
drawCicle3(R3);
glFlush ( );
}
void main (int argc, char** argv)
{
glutInit (&argc, argv);
glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB);
glutInitWindowPosition (0, 0);
glutInitWindowSize (600, 600);
glutCreateWindow ("Head monster");
init();
glutDisplayFunc (myDraw);
glutMainLoop ( );
}
Topic 6: bonus question
Include but not limited to the following pictures, and realize their shape through compound transformation

Blogger's effect:
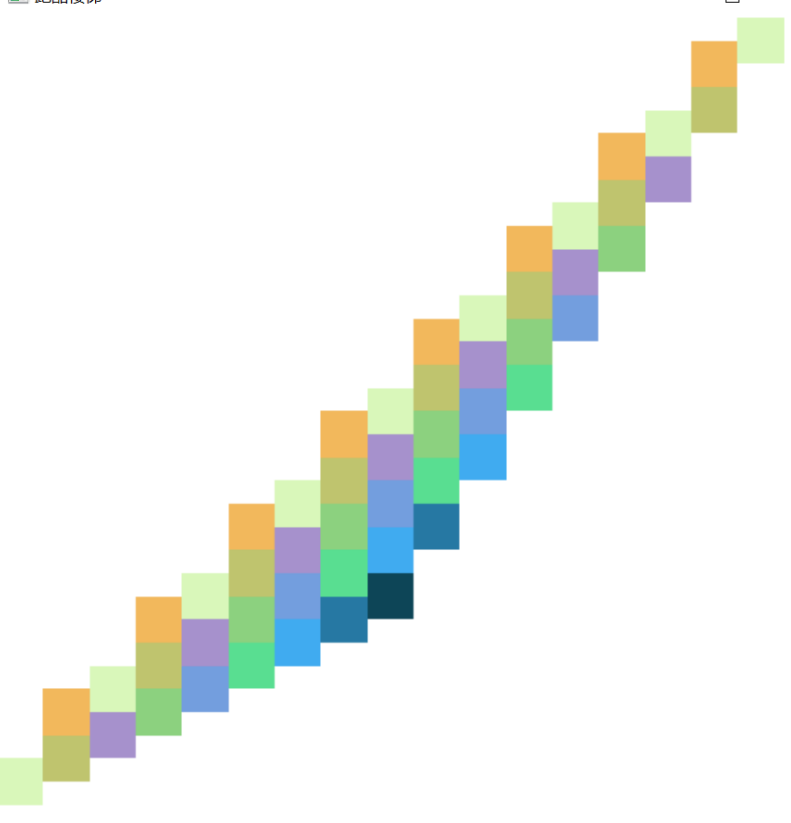
code:
#include <GL/glut.h>
#include <math.h>
float R1 = 1;
float R2 = 0.65;
float R3 = 0.5;
int i;
int j;
void init (void)
{
glClearColor (1.0, 1.0, 1.0, 0.0);
glMatrixMode (GL_PROJECTION);
gluOrtho2D (-18.0, 18.0, -18.0, 18.0); //Set the display range to be X:-5.0~5.0, Y:-5.0~5.0
glMatrixMode (GL_MODELVIEW);
}
void drawSquare(void) //Draw a square with a center at the origin and a side length of 2
{
glBegin (GL_POLYGON); //Vertex assignments need to be counterclockwise
glVertex2f (-1.0f,-1.0f);//Lower left point
glVertex2f (1.0f,-1.0f);//Lower right point
glVertex2f (1.0f, 1.0f);//Upper right point
glVertex2f (-1.0f,1.0f);//Upper left point
glEnd ( );
}
void myDraw (void)
{
int i, j;
float r = 0.05;
float g = 0.27;
float b = 0.34;
int x = -1, y = -7;
glClear(GL_COLOR_BUFFER_BIT); //empty
glLoadIdentity(); //Sets the current matrix as the identity matrix
//Middle rectangle
glPushMatrix();
glColor3f(1.0, 1.0, 0.0);
drawSquare();
glPopMatrix();
for (i = 0; i < 10; i++) {
for (j = -i; j <= i; j += 2) {
glPushMatrix();
glTranslatef(x + j + 1 * j, y + i +j*2, 0.0);
glColor3f(r, g, b);
drawSquare();
glPopMatrix();
}
r += 0.1;
g += 0.2;
b += 0.3;
if (r > 1.0)
r -= 0.23f;
if (g > 1.0)
g -= 0.45f;
if (b > 1.0)
b -= 0.67f;
}
glFlush ( );
}
void main (int argc, char** argv)
{
glutInit (&argc, argv);
glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB);
glutInitWindowPosition (0, 0);
glutInitWindowSize (600, 600);
glutCreateWindow ("Parkour stairs");
init();
glutDisplayFunc (myDraw);
glutMainLoop ( );
}
3, Description of main functions:
1,glMatrixMode():
-
In fact, this function is to declare what to do next, that is, to tell the computer that I want to operate the "what" before I want to do the next step
Parameter in "()" of glMatrixMode: GL_PROJECTION,GL_MODELVIEW and GL_TEXTURE. -
GL_ Project: projection is to operate the projection correlation, that is, to project the object onto a plane, just like our photography, to project the 3D object onto 2
On the plane of dimension. In this way, the following statements can be perspective related functions, such as glFrustum() or gluPerspective(); -
GL_MODELVIEW: the operation of the model scene. The following statement describes a model-based adaptation to set parameters. The following is used as
Functions such as gluLookAt(); -
GL_ Context: refers to the operation of texture related;
Incidentally, many operations in OpenGL are based on matrix operations, such as displacement, rotation and scaling. Therefore, the specification here is that glMatrixMode is used to specify which matrix is the current matrix, and its parameters represent the target of the operation,
- GL_ Project is an operation on the projection matrix,
- GL_MODELVIEW is the operation of model scene matrix,
- GL_ Text is the subsequent operation on the texture matrix.
2,glLoadIdentity():
Set the current matrix as the identity matrix before the transformation.
Model and view transformation mainly involves three functions:
- glTranslate(): translation transform function.
- glTranslatef(GLfloat x,GLfloat y,GLfloat z); Function function:
- Translate x units in the positive direction of the X axis (x is the signed number), y units in the positive direction of the Y axis (y is the signed number), and Z units in the positive direction of the Z axis (z is the signed number)
- Here, x, y and Z are set corresponding to the window display range given by the glOrtho2D() function.
For example, if the range of x given here is [- 5, 5], then the value of x cannot be greater than 5 or less than - 5, otherwise the object will move out of the viewing window and enter the invisible area.
- glRotate(): rotate the transform function.
- glRotatef(GLfloat angle,GLfloat x,GLfloat y,GLfloat z);
- First explain the rotation direction, make the vector from (0,0,0) to (x,y,z), hold the vector with your right hand, point your thumb to the positive direction of the vector, and the direction around your four fingers is the direction of rotation;
- For example:
glRotatef (xrot , 1.0f, 0.0f, 0.0f); // Rotate glRotatef (yrot) around the X axis,
0.0f, 1.0f, 0.0f); // Rotate about Y axis
-
Function function: rotate the angle counterclockwise with the straight line from point (0,0,0) to point (x,y,z) as the axis;
-
glScale(): scale function.
-
glScalef(GLfloat sx, GLfloat sy, GLfloat sz);
-
Function function: the model is scaled along the x, y and z axes, and the scaling ratios are sx, sy and sz respectively. sx, sy and sz are all numbers greater than 0.
-
If the size remains unchanged in a certain direction, the corresponding scaling factor needs to be set to 1, not 0.
3. glPushMatrix() and glPopMatrix(): matrix stack operation functions.
- It is the stack operation problem in the data structure, first in and last out.
- The glPushMatrix function copies the current state and puts it on the stack,
- The glPopMatrix function takes the state from the stack.
During matrix operation, we may need to copy and save a matrix first, and then restore it after a period of time.
- When we need to save, we call the glPushMatrix function, which is equivalent to putting the matrix (equivalent to a plate) on the stack.
- When you need to restore the last save, call the glPopMatrix function, which is equivalent to removing the matrix from the stack.
- First pile up the plates and then take them out.
- After you make some changes such as moving or rotating, use glPushMatrix();
OpenGL will save the transformed position and angle. - Then you can make a second move or rotation transformation, and then use glPopMatrix();
OpenGL restores the position and angle just saved. - For example:
glLoadIdentity(); glTranslatef(1,0,0);//Move right (1,0,0) glPushMatrix();//Save the current location glTranslatef(0,1,0)// Now it's (1,1,0) glPopMatrix();//So now it's back to (1,0,0) glPushMatrix();//Copy and save the matrix state before it, including all transformation states such as translation, rotation, scale and color.
1. The glPushMatrix() function needs to be placed before the drawing function (here is drawSqure()), and it is useless after that, because the previously set matrix state is lost.
2. OpenGL specifies that the capacity of the stack can accommodate at least 32 matrices. In some OpenGL implementations, the capacity of the stack actually exceeds 32.
Therefore, there is no need to worry about the capacity of the matrix.
4. glOrtho2D(): it is responsible for what kind of visual body is used to intercept the image and set the coordinate range of the display window.
"I am deeply afraid that I am not a beautiful jade, so I dare not think about it hard. But I am half convinced that I am a beautiful jade, and I am not willing to be mediocre with the rubble. So I gradually get away from the world and alienate the world. As a result, I let resentment and shame increase my cowardly self-esteem. -" records of the mountains and the moon "