summary

The Minimum Edit Distance (MED) was proposed by Vladimir Levenshtein, a Russian scientist, in 1965, hence the name Levenshtein Distance.

Levenshtein Distance is an index used to measure the similarity of two sequences in the fields of information theory, linguistics and computer science. Generally speaking, editing distance refers to two words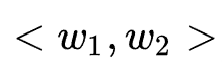Between, by one of the words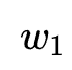Convert to another wordThe minimum number of single character editing operations required.

 

There are only three single character editing operations defined here:

• Insertion
• Delete (Deletion)
• Substitution

For example, the minimum single character editing operations required to convert the words "kitten" and "siting" from "kitten" to "siting" are:

1.kitten → sitten (substitution of "s" for "k")
2.sitten → sittin (substitution of "i" for "e")
3.sittin → sitting (insertion of "g" at the end)

Therefore, the editing distance between the words "kitten" and "sitting" is 3.

Formal definition

We will use two strings 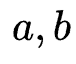   The Levenshtein Distance of is expressed as  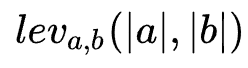, where  and    Respectively corresponding  The length of the. So, here are two strings    Levenshtein Distance, i.e    It can be described in the following mathematical language:

 

 

 

 

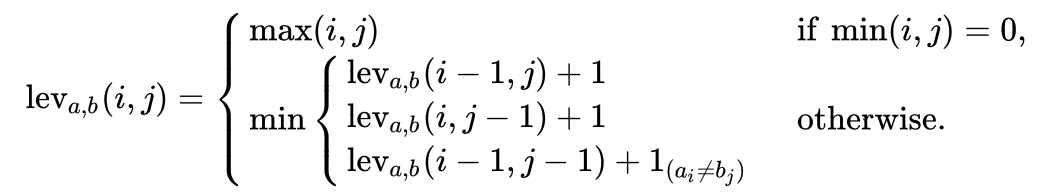
• definition  

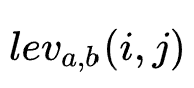•   refer to  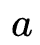  Middle front    Characters and    Middle front    The distance between characters. For ease of understanding, hereCan be seen asThe length of the. The first character index of the string here starts from 1 (in fact, 0 needs to be filled in front of the string when calculating on the table), so the final editing distance is    Distance at:  

   

   

   

   

• When 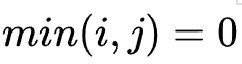   Corresponding to the string 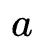 Middle front    Characters and strings  Middle front    Characters, at this time    A value of 0 indicates that one of the strings a and b is an empty string, so the conversion from a to b only needs to be performedOne single character editing operation is enough, so the editing distance between them is  , i.e    The largest of.

   

   

   

• When 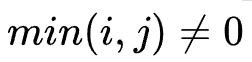   When I was young, 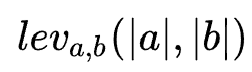 Is the minimum of the following three cases:
  1.  Indicates deletion  
  2.  Indicates insertion  
  3.  Represents substitution  

   

   

   

   

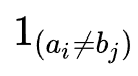•   Is an indicator function that indicates when  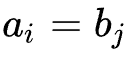  Take 0 when; When    When, its value is 1.

   

   

   

   

Process example

with 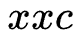   and 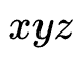   As an example, establish a matrix and record the calculated distance through the matrix: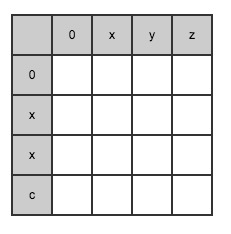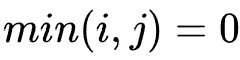

 

 

 

 

WhenWhen,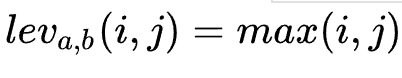, initialize the first row and first column of the matrix according to this:

First line( index = 0)initialization:
min(0, 0) = 0 ->  lev_{a, b}(0, 0) = max(0, 0) = 0
min(0, 1) = 0 ->  lev_{a, b}(0, 1) = max(0, 1) = 1
min(0, 2) = 0 ->  lev_{a, b}(0, 2) = max(0, 2) = 2
min(0, 3) = 0 ->  lev_{a, b}(0, 3) = max(0, 3) = 3

First column( index = 0)initialization:
min(0, 0) = 0 ->  lev_{a, b}(0, 0) = max(0, 0) = 0
min(1, 0) = 0 ->  lev_{a, b}(1, 0) = max(1, 0) = 1
min(2, 0) = 0 ->  lev_{a, b}(2, 0) = max(2, 0) = 2
min(3, 0) = 0 ->  lev_{a, b}(3, 0) = max(3, 0) = 3

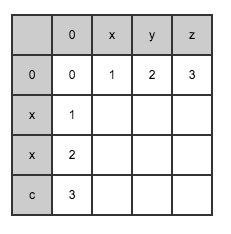
You can continue to derive the second line according to the above formula:

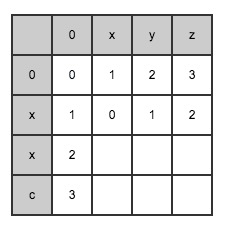
The second line (index = 1) is derived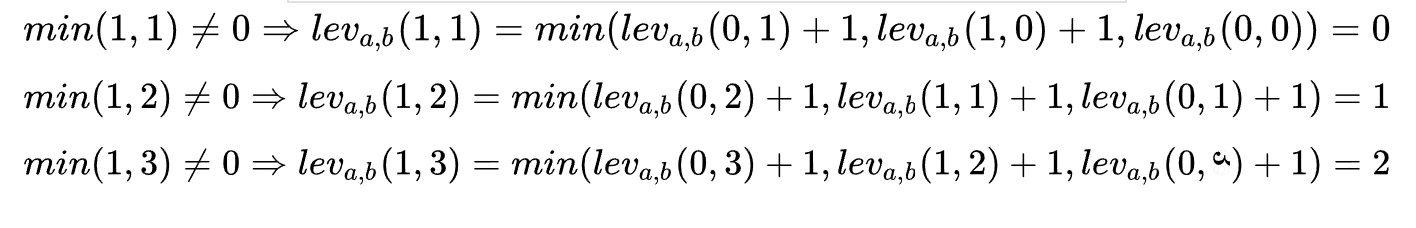

 

 

Continue the iteration and deduce in the third line (index = 2)

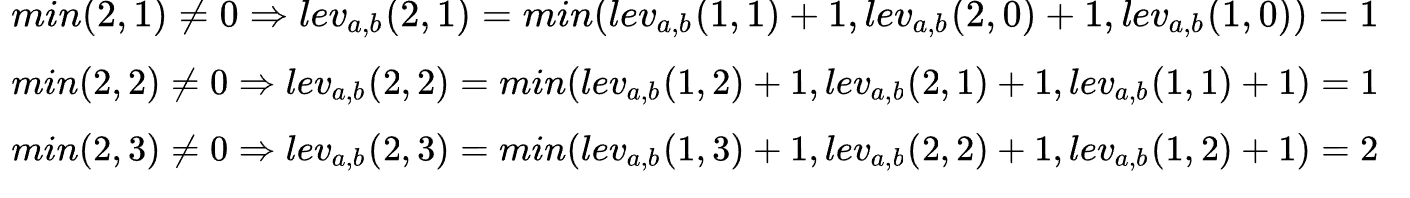
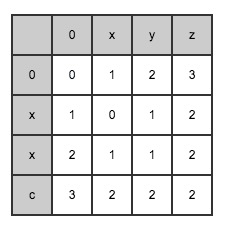
Until the final result is derived: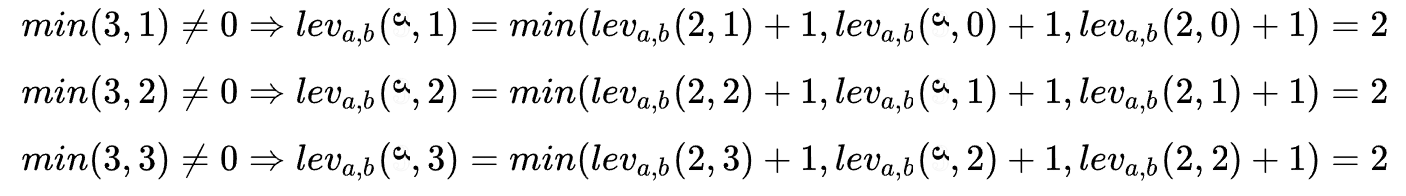

 

 

Algorithm implementation

1 recursive method

def Levenshtein_Distance_Recursive(str1, str2):

    if len(str1) == 0:
        return len(str2)
    elif len(str2) == 0:
        return len(str1)
    elif str1 == str2:
        return 0

    if str1[len(str1)-1] == str2[len(str2)-1]:
        d = 0
    else:
        d = 1
    
    return min(Levenshtein_Distance_Recursive(str1, str2[:-1]) + 1,
                Levenshtein_Distance_Recursive(str1[:-1], str2) + 1,
                Levenshtein_Distance_Recursive(str1[:-1], str2[:-1]) + d)

print(Levenshtein_Distance_Recursive("abc", "bd"))
>>>
2

2 dynamic programming
Recursion is decomposed from the back to the front. The opposite is to calculate from the front to the back and gradually deduce the final result. This method is called dynamic programming. Dynamic programming is very suitable for problems with overlapping computing nature, but a large number of intermediate computing results will be stored in this process. A good dynamic programming algorithm will minimize the spatial complexity.

def Levenshtein_Distance(str1, str2):
    """
    Calculation string str1 and str2 Edit distance
    :param str1
    :param str2
    :return:
    """
    matrix = [[ i + j for j in range(len(str2) + 1)] for i in range(len(str1) + 1)]

    for i in range(1, len(str1)+1):
        for j in range(1, len(str2)+1):
            if(str1[i-1] == str2[j-1]):
                d = 0
            else:
                d = 1
            
            matrix[i][j] = min(matrix[i-1][j]+1, matrix[i][j-1]+1, matrix[i-1][j-1]+d)

    return matrix[len(str1)][len(str2)]


print(Levenshtein_Distance("abc", "bd"))

>>>
2

Application and thinking

Editing distance is a basic NLP algorithm to measure text similarity. It can be used as one of the important features of text similarity tasks. It can be applied to many aspects, such as spell checking, paper duplication checking, gene sequence analysis and so on. However, its disadvantages are also obvious. The algorithm is calculated based on the text's own structure, and there is no way to obtain the semantic information.

Because the matrix needs to be used, the space complexity is O(MN). This can achieve good performance when the two strings are relatively short. However, if the string is relatively long, it needs a lot of space to store the matrix. For example, if the two strings are 20000 characters, the size of the LD matrix is 20000 * 20000 * 2=800000000 Byte=800MB.

reference

[1] https://blog.csdn.net/ghsau/article/details/78903076
[2] https://en.wikipedia.org/wiki/Levenshtein_distance
[3] https://www.dreamxu.com/books/dsa/dp/edit-distance.html
[4] String similarity (edit distance algorithm) - simple book