1. Introduction to DNA Chaotic System Image Encryption

Image encryption based on DNA encoding uses DNA encoding by dividing the image into blocks, generating a key through the CHEN hyperchaos system, and decoding the encrypted image after special DNA operations.
Logistic chaos is very simple, not to mention how complex it is.
The Logistic function is a dynamic system derived from a population statistic and its system equation is as follows:
X(k+1) = u * X(k) * [1 - X(k)],(k=0,1,...,n)
Do not care how this equation comes out first, if you feel uncomfortable, go to Baidu yourself. You can see that the equation is nonlinear and iterative. To use it, we need to know two things:
(1) Initial value: X(0)
(2) Parameters: u

Why can this equation be called chaos? When is it a chaotic system? This is also conditional:

① 0 < X(0) < 1

② 3.5699456... < u <=4

When these two conditions are met, the Logistic function works in a chaotic state. How did these two conditions come to Baidu? Here we only talk about algorithms and implementation. What is chaotic state: as its name implies, it is an disordered, unpredictable, chaotic, untouchable, and untouchable state. What happens when a chaotic state occurs? Let's take the following parameters as an example:

① X(0) = 0.1

② u = 4

When we iterate n times, we get n values like X(1), X(2),..., X(n). So this is a chaotic sequence, a one-dimensional temporary sequence called sequence A, which is what we want to get. In MATLAB, we can see that X(i) (i=1,2,..., n) is between (0,1) - which is a good feature, just like the image gray values are between (0,255). Then we normalize this one-dimensional sequence to (0,255) to get sequence B.
Let's look at the encryption process again. For an MN-sized image (also known as a Picture), we need to generate a matrix of the same size to encrypt it. So, just iterate MN times to get sequence A, then convert it to sequence B, where sequence B is one-dimensional and converts it to a two-dimensional matrix of M*N So if you use Fuck and Picutre to XOR, you get a new image called Rod, which completes an image encryption process, and the encrypted image is Rod.

Rod=Picture_Fuck(denotes XOR)

So the secret key in our hands is: u, X(0)

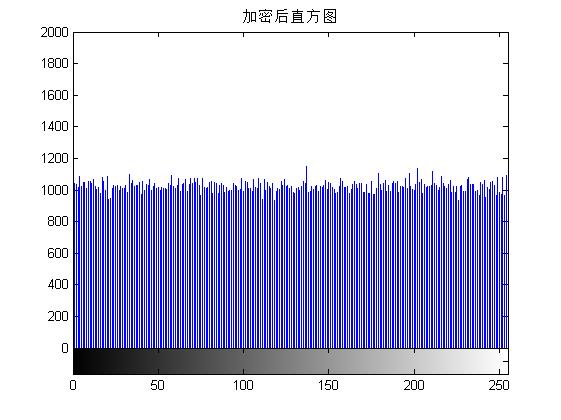
This encryption method is called sequence encryption, and you can see that it changes the grayscale of the lower pixel (the histogram changes) without changing its position. The same applies to decryption: Picture = Rod_Fuck.

2. Partial Source Code

clear;clc;
I=imread('lena.bmp','bmp');         %Read image information
figure;imshow(I);title('Original Picture');
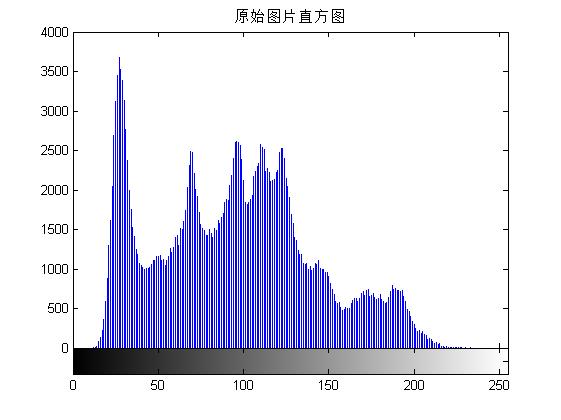
figure;imhist(I);title('Original Picture Histogram');
axis([0 255 0 4000]);
[M,N]=size(I);                      %Assign rows and columns of images to M,N
t=4;    %Block size

%% Original Picture Information Entropy
T1=imhist(I);   %Statistical image gray value from 0~255 Distribution, stored to T1
S1=sum(T1);     %Calculate the gray value of the whole image
xxs1=0;
for i=1:256
    pp1=T1(i)/S1;   %Percentage of each gray value, the probability of each gray value
    if pp1~=0
        xxs1=xxs1-pp1*log2(pp1);
    end
end

%% Correlation analysis of adjacent pixels in original image
%{
Randomize first at 0~M-1 Rows and 0~N-1 The column selects 1000 pixel points.
When calculating the horizontal correlation, select the adjacent right-hand point for each point.
When calculating the vertical correlation, select the adjacent lower point of each point.
When calculating the diagonal correlation, select the adjacent lower right point for each point.
%}
NN=1000;    %Randomly take 1000 pairs of pixels
x1=ceil(rand(1,NN)*(M-1));      %Generate 1000 1~M-1 As rows
y1=ceil(rand(1,NN)*(N-1));      %Generate 1000 1~N-1 Random integers of
EX1=0;EY1_SP=0;DX1=0;DY1_SP=0;COVXY1_SP=0;    %Variables needed to calculate horizontal correlation
EY1_CZ=0;DY1_CZ=0;COVXY1_CZ=0;                %vertical
EY1_DJX=0;DY1_DJX=0;COVXY1_DJX=0;             %diagonal
I=double(I);
for i=1:NN
    %First Pixel Point E，The first pixel computed when horizontal, vertical, and diagonal E Same, unified EX1 Express
    EX1=EX1+I(x1(i),y1(i)); 
    %Of the second pixel E，Horizontal, Vertical, Diagonal E Correspond to each other EY1_SP,EY1_CZ,EY1_DJX
    EY1_SP=EY1_SP+I(x1(i),y1(i)+1);
    EY1_CZ=EY1_CZ+I(x1(i)+1,y1(i));
    EY1_DJX=EY1_DJX+I(x1(i)+1,y1(i)+1);
end
%Reduce the number of operations by uniformly dividing by 1,000 pixel points outside the loop
EX1=EX1/NN;
EY1_SP=EY1_SP/NN;
EY1_CZ=EY1_CZ/NN;
EY1_DJX=EY1_DJX/NN;
for i=1:NN
    %First Pixel Point D，Calculates the first pixel point when horizontal, vertical, and diagonal D Same, unified DX Express
    DX1=DX1+(I(x1(i),y1(i))-EX1)^2;
    %Of the second pixel D，Horizontal, Vertical, Diagonal E Correspond to each other DY1_SP,DY1_CZ,DY1_DJX
    DY1_SP=DY1_SP+(I(x1(i),y1(i)+1)-EY1_SP)^2;
    DY1_CZ=DY1_CZ+(I(x1(i)+1,y1(i))-EY1_CZ)^2;
    DY1_DJX=DY1_DJX+(I(x1(i)+1,y1(i)+1)-EY1_DJX)^2;
    %Computation of correlation function between two adjacent pixel points, horizontal, vertical and diagonal
    COVXY1_SP=COVXY1_SP+(I(x1(i),y1(i))-EX1)*(I(x1(i),y1(i)+1)-EY1_SP);
    COVXY1_CZ=COVXY1_CZ+(I(x1(i),y1(i))-EX1)*(I(x1(i)+1,y1(i))-EY1_CZ);
    COVXY1_DJX=COVXY1_DJX+(I(x1(i),y1(i))-EX1)*(I(x1(i)+1,y1(i)+1)-EY1_DJX);
end
%Reduce the number of operations by uniformly dividing by 1,000 pixel points outside the loop
DX1=DX1/NN;
DY1_SP=DY1_SP/NN;
DY1_CZ=DY1_CZ/NN;
DY1_DJX=DY1_DJX/NN;
COVXY1_SP=COVXY1_SP/NN;
COVXY1_CZ=COVXY1_CZ/NN;
COVXY1_DJX=COVXY1_DJX/NN;
%Correlation of Horizontal, Vertical and Diagonal Lines
RXY1_SP=COVXY1_SP/sqrt(DX1*DY1_SP);
RXY1_CZ=COVXY1_CZ/sqrt(DX1*DY1_CZ);
RXY1_DJX=COVXY1_DJX/sqrt(DX1*DY1_DJX);

%% 1.Zero Complement
%Completing the number of rows and columns of an image can be t The number divided by an integer, t Is the size of the tile.
M1=mod(M,t);
N1=mod(N,t);
if M1~=0
    I(M+1:M+t-M1,:)=0;
end
if N1~=0
    I(:,N+1:N+t-N1)=0;
end
[M,N]=size(I);  %Number of rows and columns after zeroing
SUM=M*N;

%% 2.produce Logistic Chaotic Sequence
u=3.99;     %Logistic parameterμ，Custom-made 3.99
x0=sum(I(:))/(255*SUM);     %Calculated Logistic initial value x0
x0=floor(x0*10^4)/10^4;     %Keep 4 decimal places
p=zeros(1,SUM+1000);        %Preallocated memory
p(1)=x0;
for i=1:SUM+999                 %Conduct SUM+999 Secondary cycle, total SUM+1000 Points (including initial values)
    p(i+1)=u*p(i)*(1-p(i));
end
p=p(1001:length(p));            %Remove the first 1000 points for better randomness

%% 3.take p Sequence Transform to 0~255 Range integer, converted to M*N Two-dimensional matrix R
p=mod(ceil(p*10^3),256);
R=reshape(p,N,M)';  %Conversion M That's ok N Random Matrix of Columns R

%% 4.solve Chen Hyperchaotic system
%Find Four Initial Values X0,Y0,Z0,H0
r=(M/t)*(N/t);      %r Number of tiles
%Find four initial values
X0=sum(sum(bitand(I,3)))/(3*SUM);
Y0=sum(sum(bitand(I,12)/4))/(3*SUM);
Z0=sum(sum(bitand(I,48)/16))/(3*SUM);
H0=sum(sum(bitand(I,192)/64))/(3*SUM);
%Keep four decimal places
X0=floor(X0*10^4)/10^4;
Y0=floor(Y0*10^4)/10^4;
Z0=floor(Z0*10^4)/10^4;
H0=floor(H0*10^4)/10^4;
%Solve according to initial value Chen Four chaotic sequences derived from the hyperchaotic system
A=chen_output(X0,Y0,Z0,H0,r);   
X=A(:,1);
X=X(1502:length(X));        %Eliminate the first 1501 items to get better randomness (1500 points more are calculated to solve the subfunctions of Chen's system)
Y=A(:,2);
Y=Y(1502:length(Y));
Z=A(:,3);
Z=Z(1502:length(Z));
H=A(:,4);
H=H(1502:length(H));

%% 5.DNA Code
%X,Y Decide separately I and R Of DNA There are 8 encoding methods, 1~8
%Z There are three ways to determine the operation, 0~2，0 Represents plus, 1 minus, 2 XOR
%H Express DNA There are 8 decoding methods, 1~8
X=mod(floor(X*10^4),8)+1;
Y=mod(floor(Y*10^4),8)+1;
Z=mod(floor(Z*10^4),3);
H=mod(floor(H*10^4),8)+1;
e=N/t;  %e Indicates how many blocks each row can be divided into
Q1=DNA_bian(fenkuai(t,I,1),X(1));
Q2=DNA_bian(fenkuai(t,R,1),Y(1));
Q_last=DNA_yunsuan(Q1,Q2,Z(1));
Q(1:t,1:t)=DNA_jie(Q_last,H(1));
for i=2:r
    Q1=DNA_bian(fenkuai(t,I,i),X(i));   %Press each block of the original image X Corresponding serial number DNA Code
    Q2=DNA_bian(fenkuai(t,R,i),Y(i));   %Yes R Each tile by Y Corresponding serial number DNA Code
    Q3=DNA_yunsuan(Q1,Q2,Z(i));         %Press on the two coded blocks above Z Corresponding serial number DNA operation
    Q4=DNA_yunsuan(Q3,Q_last,Z(i));     %The result of the operation is pressed in the previous block Z The corresponding sequence number is calculated again, called diffusion
    Q_last=Q4;
    xx=floor(i/e)+1;
    yy=mod(i,e);
    if yy==0
        xx=xx-1;
        yy=e;
    end
    Q((xx-1)*t+1:xx*t,(yy-1)*t+1:yy*t)=DNA_jie(Q4,H(i));    %Combine each block into a complete graph Q
end
Q=uint8(Q);
imwrite(Q,'Encrypted lena.bmp','bmp');        
figure;imshow(Q);title('Encrypted picture');
figure;imhist(Q);title('Encrypted Histogram');
axis([0 255 0 2000]);

%% Encrypted Information Entropy
T2=imhist(Q);
S2=sum(T2);
xxs2=0;
for i=1:256
    pp2=T2(i)/S2;
    if pp2~=0
        xxs2=xxs2-pp2*log2(pp2);
    end
end

%% Correlation Analysis of Adjacent Images of Encrypted Images
%{
Randomize first at 0~M-1 Rows and 0~N-1 The column selects 1000 pixel points.
When calculating the horizontal correlation, select the adjacent right-hand point for each point.
When calculating the vertical correlation, select the adjacent lower point of each point.
When calculating the diagonal correlation, select the adjacent lower right point for each point.
%}
Q=double(Q);
EX2=0;EY2_SP=0;DX2=0;DY2_SP=0;COVXY2_SP=0;    %level
EY2_CZ=0;DY2_CZ=0;COVXY2_CZ=0;    %vertical
EY2_DJX=0;DY2_DJX=0;COVXY2_DJX=0;   %diagonal
for i=1:NN
    %First Pixel Point E，The first pixel computed when horizontal, vertical, and diagonal E Same, unified EX2 Express
    EX2=EX2+Q(x1(i),y1(i));
    %Of the second pixel E，Horizontal, Vertical, Diagonal E Correspond to each other EY2_SP,EY2_CZ,EY2_DJX
    EY2_SP=EY2_SP+Q(x1(i),y1(i)+1);
    EY2_CZ=EY2_CZ+Q(x1(i)+1,y1(i));
    EY2_DJX=EY2_DJX+Q(x1(i)+1,y1(i)+1);
end
%Reduce the number of operations by uniformly dividing by 1,000 pixel points outside the loop
EX2=EX2/NN;
EY2_SP=EY2_SP/NN;
EY2_CZ=EY2_CZ/NN;
EY2_DJX=EY2_DJX/NN;
for i=1:NN
    %First Pixel Point D，Calculates the first pixel point when horizontal, vertical, and diagonal D Same, unified DX2 Express
    DX2=DX2+(Q(x1(i),y1(i))-EX2)^2;
    %Of the second pixel D，Horizontal, Vertical, Diagonal E Correspond to each other DY2_SP,DY2_CZ,DY2_DJX
    DY2_SP=DY2_SP+(Q(x1(i),y1(i)+1)-EY2_SP)^2;
    DY2_CZ=DY2_CZ+(Q(x1(i)+1,y1(i))-EY2_CZ)^2;
    DY2_DJX=DY2_DJX+(Q(x1(i)+1,y1(i)+1)-EY2_DJX)^2;
    %Computation of correlation function between two adjacent pixel points, horizontal, vertical and diagonal
    COVXY2_SP=COVXY2_SP+(Q(x1(i),y1(i))-EX2)*(Q(x1(i),y1(i)+1)-EY2_SP);
    COVXY2_CZ=COVXY2_CZ+(Q(x1(i),y1(i))-EX2)*(Q(x1(i)+1,y1(i))-EY2_CZ);
    COVXY2_DJX=COVXY2_DJX+(Q(x1(i),y1(i))-EX2)*(Q(x1(i)+1,y1(i)+1)-EY2_DJX);
end
%Reduce the number of operations by uniformly dividing by 1,000 pixel points outside the loop
DX2=DX2/NN;
DY2_SP=DY2_SP/NN;
DY2_CZ=DY2_CZ/NN;
DY2_DJX=DY2_DJX/NN;
COVXY2_SP=COVXY2_SP/NN;
COVXY2_CZ=COVXY2_CZ/NN;
COVXY2_DJX=COVXY2_DJX/NN;
%Correlation of Horizontal, Vertical and Diagonal Lines
RXY2_SP=COVXY2_SP/sqrt(DX2*DY2_SP);
RXY2_CZ=COVXY2_CZ/sqrt(DX2*DY2_CZ);
RXY2_DJX=COVXY2_DJX/sqrt(DX2*DY2_DJX);

%% Output Data Information
disp('Encryption succeeded');  
disp(['Key 1:μ=',num2str(u),'     Key 2: x0=',num2str(x0),'    Key 3: x(0)=',num2str(X0)]);
disp(['Key 4: y(0)=',num2str(Y0),'  Key 2: z(0)=',num2str(Z0),'   Key 3: h(0)=',num2str(H0)]);
disp(['Original Picture Information Entropy=',num2str(xxs1),'  Encrypted Picture Information Entropy=',num2str(xxs2)]);
disp(['Relevance of original picture:','  Horizontal correlation=',num2str(RXY1_SP),'  Vertical correlation=',num2str(RXY1_CZ),'  Diagonal correlation=',num2str(RXY1_DJX)]);
disp(['Encrypted picture correlation:','  Horizontal correlation=',num2str(RXY2_SP),'  Vertical correlation=',num2str(RXY2_CZ),'  Diagonal correlation=',num2str(RXY2_DJX)]);
 

3. Operation results

4. matlab Versions and References

1 matlab version
2014a

2 References
[1] Cai Limei. Image Processing in MATLAB--Theory, Algorithms and Example Analysis [M]. Tsinghua University Press, 2020.
[2] Yang Dan, Zhao Haibin, Longzhe. MATLAB image processing example [M]. Tsinghua University Press, 2013.
[3] Weekly items. MATLAB image processing and GUI design [M]. Tsinghua University Press, 2013.
[4] Liu Chenglong. Proficient in MATLAB image processing [M]. Tsinghua University Press, 2015.