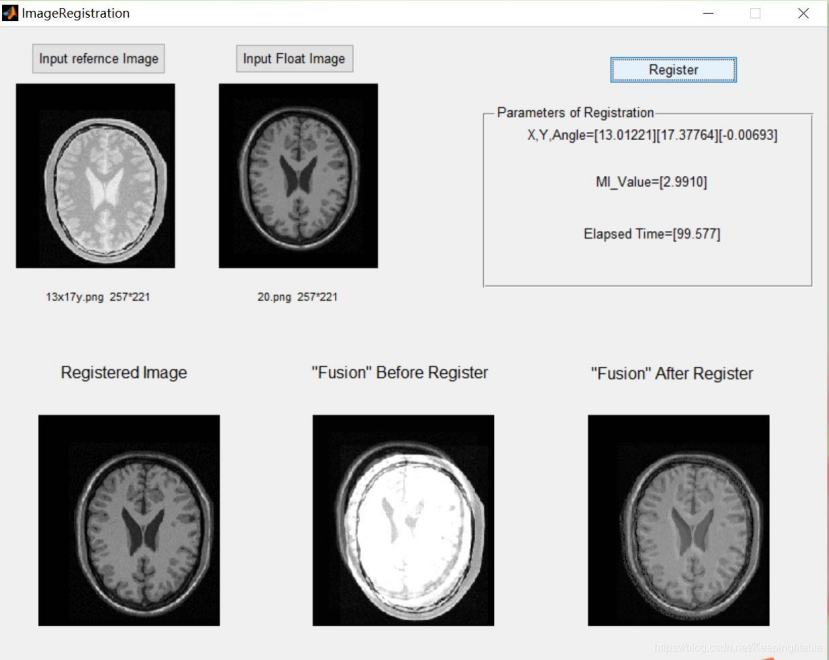
Image registration based on matlab GUI Powell+ant colony algorithm
1. Introduction
1 The origin and development of ant colony algorithm (ACA)
Marco Dorigo et al. found that ants can quickly find their target by exchanging their foraging information by secreting a biohormone called pheromone when they are searching for food. In 1991, in his PhD paper, a new intelligent optimization algorithm based on ant population, Ant system (AS), was first systematically proposed.Later, various improvements have been made and applied to a wider range of fields, such as coloring problem, secondary assignment problem, job scheduling problem, vehicle routing problem, shop floor job scheduling problem, network routing problem, large-scale integrated circuit design, etc. In recent years, M.Dorigo et al. have further developed ant algorithm into a general one.Ant Colony Optimization (ACO) is the optimization technology used, and all algorithms that conform to the ACO framework are called ACO algorithm.
Specifically, ants begin to look for food without telling them where it is. When a food is found, it releases a volatile secretion called pheromone (known as pheromone, which evaporates over time and the concentration of pheromone indicates the distance along the path).Pheromones can be perceived by other ants to play a guiding role. When pheromones are found on multiple paths, ants will usually prefer paths with high concentrations of pheromones, which results in higher concentrations of path pheromones, forming a positive feedback. Some ants do not always repeat the same path as other ants, and they will open up new paths if they do.Roads are shorter than other roads, so gradually more ants are attracted to this shorter road. Finally, over time, a shortest path may appear to be repeated by most ants. Ultimately, the path with the highest concentration of pheromones is the best one that is ultimately chosen by ants.
Compared with other algorithms, ant colony algorithm is a younger algorithm, which has the characteristics of distributed computing, no center control, asynchronous and indirect communication between individuals, and is easy to combine with other optimization algorithms. After many people's constant exploration, a variety of improved ant colony algorithm has been developed today, but the principle of ant colony algorithm is still the backbone.
Solving Principle of Ant Colony Algorithm
Based on the above description of ants'foraging behavior, the algorithm mainly simulates the following aspects of foraging behavior:
(1) The simulated scene contains two pheromones, one for home and one for food location, and both of them are volatilizing at a certain rate.
(2)Each ant can only perceive information in a small part of its surroundings. When it is looking for food, if it is within its perception range, it can go directly. If it is not within its perception range, it has to move toward a place with more pheromones. An ant can have a small probability of not going to a place with more pheromones and create a new path. This small probability event is very important and represents a search.Innovation in the way is important for finding better solutions.
(3) The rules for ants to return to their nests are the same as those for finding food.
(4) When an ant moves, it will first follow the guidance of the pheromone. Without the guidance of the pheromone, it will walk in its own direction of inertia, but it also has a certain chance to change direction. The ant can also remember the way it has traveled and avoid repeating a place.
(5)Ants leave the most pheromones when they find food, and then the farther away they leave the food, the fewer. Finding nests leaves the same amount of pheromones as food. Ant colony algorithm has the following characteristics: positive feedback algorithm, concurrency algorithm, strong robustness, probability-based global search, independent of strict mathematical properties, long search time, and prone to stop.Stop phenomena.
Ant transfer probability formula: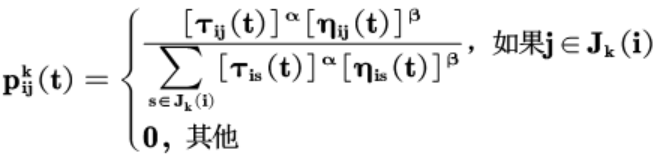
In the formula: is the probability that ant K will move from city I to j; alpha, beta are the relative importance of pheromones and heuristic factors; the amount of pheromones on the edge (i,j); the heuristic factor; the city that allows selection for ant K next step. The above formula is the updated formula of pheromones in the ant system, which is the edgeThe amount of pheromone on (i,j); Rho is the evaporation coefficient of the pheromone, 0 < Rho < 1; the amount of pheromone left on the edge (i,j) by the k-th ant in this iteration; Q is a normal coefficient; and the length of the path of the k-th ant in this tour.
In the ant system, the pheromone update formula is: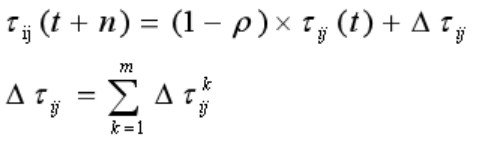
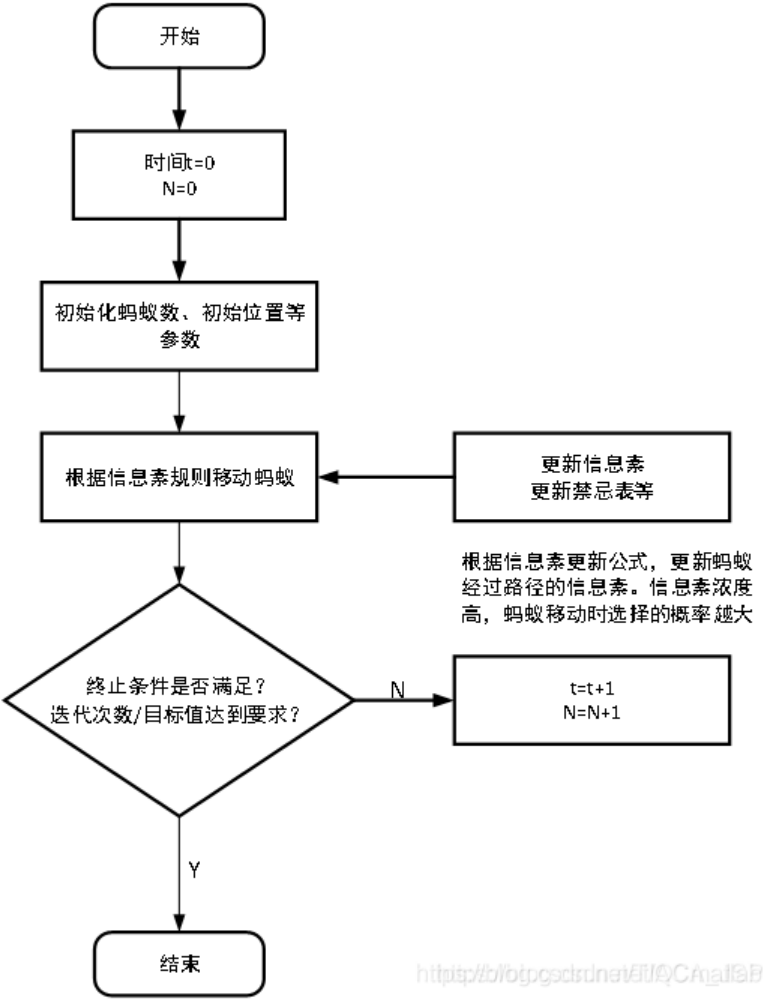
3Solving steps of ant colony algorithm:
(1) Initialization parameters need to be initialized at the beginning of calculation, such as ant colony size (number of ants) m, pheromone importance factor alpha, heuristic importance factor beta, pheromone silver rho, total pheromone release Q, maximum iteration iter_max, initial iteration number iter=1.
(2) Build a solution space to randomly place each ant at a different starting point. For each ant K (k=1,2,3...m), calculate its next city to visit according to (2-1) until all ants have visited all cities.
(3) Update Information Sum calculates each ant's path length Lk(k=1,2,..., m), records the optimal solution (shortest path) in the current iteration number, and updates the concentration of pheromone on each city connection path according to the formulas (2-2) and (2-3).
(4) Determine whether to terminate if iter<iter_max, then make iter=iter+1, empty the record table of the ant's path, and return to step 2; otherwise, terminate the calculation and output the optimal solution.
(5) Determine whether to terminate if iter<iter_max, let iter=iter+1, empty the record table of the ant's path, and return to step 2; otherwise, terminate the calculation and output the optimal solution. 3. Determine whether to terminate if iter<iter_max, let iter=iter+1, empty the record table of the ant's path, and return to step 2; otherwise, terminate the calculation and output the optimal solution.
Source Code
function varargout = ImageRegistration(varargin)
% IMAGEREGISTRATION M-file for ImageRegistration.fig
% IMAGEREGISTRATION, by itself, creates a new IMAGEREGISTRATION or raises the existing
% singleton*.
%
% H = IMAGEREGISTRATION returns the handle to a new IMAGEREGISTRATION or the handle to
% the existing singleton*.
%
% IMAGEREGISTRATION('CALLBACK',hObject,eventData,handles,...) calls the local
% function named CALLBACK in IMAGEREGISTRATION.M with the given input arguments.
%
% IMAGEREGISTRATION('Property','Value',...) creates a new IMAGEREGISTRATION or raises the
% existing singleton*. Starting from the left, property value pairs are
% applied to the GUI before ImageRegistration_OpeningFcn gets called. An
% unrecognized property name or invalid value makes property
% application
% stop. All inputs are passed to ImageRegistration_OpeningFcn via varargin.
%
% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one
% instance to run (singleton)".
%
% See also: GUIDE, GUIDATA, GUIHANDLES
% Edit the above text to modify the response to help ImageRegistration
% Last Modified by GUIDE v2.5 24-May-2021 17:01:50
% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name', mfilename, ...
'gui_Singleton', gui_Singleton, ...
'gui_OpeningFcn', @ImageRegistration_OpeningFcn, ...
'gui_OutputFcn', @ImageRegistration_OutputFcn, ...
'gui_LayoutFcn', [] , ...
'gui_Callback', []);
if nargin && ischar(varargin{1})
gui_State.gui_Callback = str2func(varargin{1});
end
if nargout
[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
gui_mainfcn(gui_State, varargin{:});
end
% End initialization code - DO NOT EDIT
addpath(pwd);
% --- Executes just before ImageRegistration is made visible.
function ImageRegistration_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% varargin command line arguments to ImageRegistration (see VARARGIN)
% Choose default command line output for ImageRegistration
handles.output = hObject;
% Update handles structure
guidata(hObject, handles);
% UIWAIT makes ImageRegistration wait for user response (see UIRESUME)
% uiwait(handles.figure1);
% --- Outputs from this function are returned to the command line.
function varargout = ImageRegistration_OutputFcn(hObject, eventdata, handles)
% varargout cell array for returning output args (see VARARGOUT);
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% Get default command line output from handles structure
varargout{1} = handles.output;
% --- Executes on button press in pushbutton1.
function pushbutton1_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton1 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
clc
%%%%%%%%%%%%%%%call OpenImage.m Read in the reference image and get the file name, image size%%%%%%%%%%%%
[fname,pname,index]=uigetfile({'*.jpg;*.bmp;*.png;*.tif;*.gif;*.jpeg'},'Select Reference Image');
if index
name=[pname fname];
temp=imread(name);
[m,n]=size(temp);
m=num2str(m);
n=num2str(n);
imsize=[' ',m,'*',n];
handles.ImsizeI=imsize;
handles.filenameI=name;
handles.names_dispI=[fname,imsize];
end
set(handles.text2,'String',handles.names_dispI);
guidata(hObject,handles);
%%%%%%%%%%%%%%%%%%Display reference image%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
axes(handles.axes1)
I=imread(handles.filenameI);
save I;
imshow(I)
figure(5)
imshow(I)
% --- Executes on button press in pushbutton2.
function pushbutton2_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton2 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
clc
%%%%%%%%%%%call OpenImage.m Read in floating image and get file name, image size%%%%%%%%%%
[fname,pname,index]=uigetfile({'*.jpg;*.bmp;*.png;*.tif;*.gif;*.jpeg'},'Select Floating Image');
if index
name=[pname fname];
temp=imread(name);
[m,n]=size(temp);
m=num2str(m);
n=num2str(n);
imsize=[' ',m,'*',n];
handles.ImsizeJ=imsize;
handles.filenameJ=name;
handles.names_dispJ=[fname,imsize];
end
set(handles.text3,'String',handles.names_dispJ);
guidata(hObject,handles);
%%%%%%%%%%%%%%%%%%Show floating images%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
axes(handles.axes2)
J=imread(handles.filenameJ);
imshow(J)
figure(6)
imshow(J)
% --- Executes on button press in pushbutton3.
function pushbutton3_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton3 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
clc
%%%%%%%%%%%%%%%%Detect whether reference images and floating images have been entered%%%%%%%%%%%%%%%%%%%%%%%%%%
axesIbox=get(handles.axes1,'box');
axesJbox=get(handles.axes2,'box');
if strcmp(axesIbox,'off')||strcmp(axesJbox,'off')
errordlg('Please select Image for Registration','Error')
error('NO Image!')
end
%%%%%%%%%%%%%%%Detect whether the reference image and floating image are the same size%%%%%%%%%%%%%%%%%%%%%%%%%
handles.isSameSizeIJ=strcmp(handles.ImsizeI,handles.ImsizeJ);
if handles.isSameSizeIJ~=1
errordlg('Please select the Same Size Image','Error')
error('Image Size doesn"t match!')
end
%%%%%%%%%%%%%Read in and copy images, one for registration and one for post-registration output%%%%%%%%%
I1=imread(handles.filenameI);
J1=imread(handles.filenameJ);
%%%%%%%%%%%%%"Fusion" showing pre-registration reference image and floating image"Design sketch%%%%%%%%%%%%%%%%%%%%
axes(handles.axes4)
imshow(uint8(I+J))
%%%%%%%%%%%%%%%Call function GLPF.m(Gauss low-pass filter),Complete Gauss Low Pass Preprocessing%%%%%%%%%%%%%
[I,J]=GLPF(handles);
handles.I=I;
%%%%%%%%%%%%%%Call function Powell.m,Implement image registration%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
tic
RegistrationParameters=Powell(handles);
%RegistrationParameters=AntColony(handles);
%RegistrationParameters=AntColonyimprove(handles);
toc
ElapsedTime=toc;
%%%%%%%%%%%%%%Display registration results%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
handles.RegistrationParameters=RegistrationParameters;
y=RegistrationParameters(1);
x=RegistrationParameters(2);
ang=RegistrationParameters(3);
RegistrationResult=sprintf('X,Y,Angle=[%.5f][%.5f][%.5f]',x,y,ang);
MI_Value=RegistrationParameters(4);
MI_Value=sprintf('MI_Value=[%.4f]',MI_Value);
ElapsedTime=sprintf('Elapsed Time=[%.3f]',ElapsedTime);
axes(handles.axes5)
[FusionImage,RegistrationImage]=Fusion(handles);
imshow(FusionImage)
axes(handles.axes3)
imshow(RegistrationImage)
figure(7)
imshow(RegistrationImage)
set(handles.text8,'string',RegistrationResult);
set(handles.text9,'string',MI_Value);
set(handles.text10,'string',ElapsedTime);3. Operation results