Matlab image zooming

The function code of Matlab is as follows:

clc
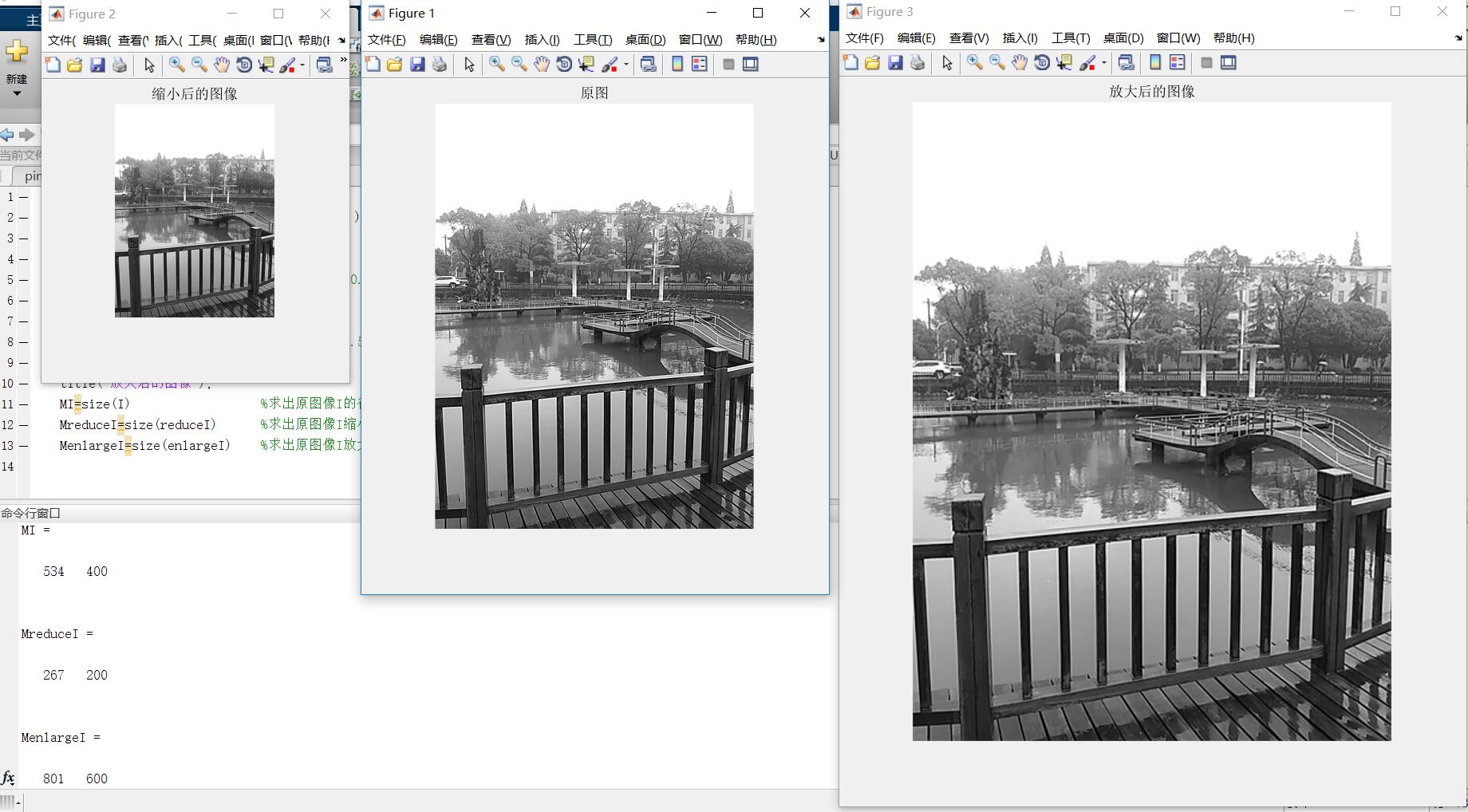
I=rgb2gray(imread('Campus-scenery2sk.JPG'));
figure,imshow(I);
title('Original');
reduceI=imresize(I,0.5);     %Original imageInarrow0.5times
figure,imshow(reduceI);
title('Reduced image');
enlargeI=imresize(I,1.5);   %Original imageIenlarge1.5times
figure,imshow(enlargeI);
title('Enlarged image');
MI=size(I)                  %Find the original imageIAnd display in the command window
MreduceI=size(reduceI)      %Find the original imageIThe reduced image row and column is displayed in the command window
MenlargeI=size(enlargeI)    %Find the original imageIEnlarged image row and column and displayed in the command window

The result of function operation is as follows:
-

Function description in the program:
       B=imresize(A,scale,method);
A is the image to be scaled, and scale is the multiple of scaling. Method is the interpolation method used in scaling. The default value is nearest neighbor interpolation.
Let (x0,y0) be a point on the original image, and we will zoom it. Let's set the zoom multiple in X direction as Sx, and let's set the zoom multiple in y direction as sy, and (x1, y1) as the pixel coordinates after zooming, which is expressed by matrix transformation as follows:
       [x1y11]=[x0y01]⎡⎣⎢Sx000Sy0001⎤⎦⎥=[x0∗Sxy0∗Sy1];
Its inverse operation is:
       [x0y01]=[x1y11]⎡⎣⎢1/Sx0001/Sy0001⎤⎦⎥=[x1/Sxy1/Sy1];
From its inverse operation, we can see that in the zoomed image calculated according to the zooming formula, some mapping source coordinates may not be integers, so the position of the corresponding pixel cannot be found. For example, when Sx=Sy=2, the image is magnified twice, and the (1,0) pixel in the magnified image corresponds to (0.5,0) in the original image. This coordinate is not an integer coordinate position, so it is impossible to extract its gray value naturally. So we need to approximate the coordinates, such as the nearest neighbor interpolation, which is the default interpolation method of the reduce() function.

I understand it by myself bilinear interpolation The image scaling function imscale() is written as follows:

function A = imscale(B,S)   %Define scaling functions,BIs the source image,AFor the target image,SIs the zoom factor
[r,c] = size(B);
nr= round(r*S);             %According to the result of multiplying the magnification by the number of original lines, the rounded value is taken as the new line
nc= round(c*S);             %According to the result of multiplying the magnification by the number of original columns, the rounded value is taken as the new column
A = zeros(nr,nc);           %Generating target image matrix with new row and column
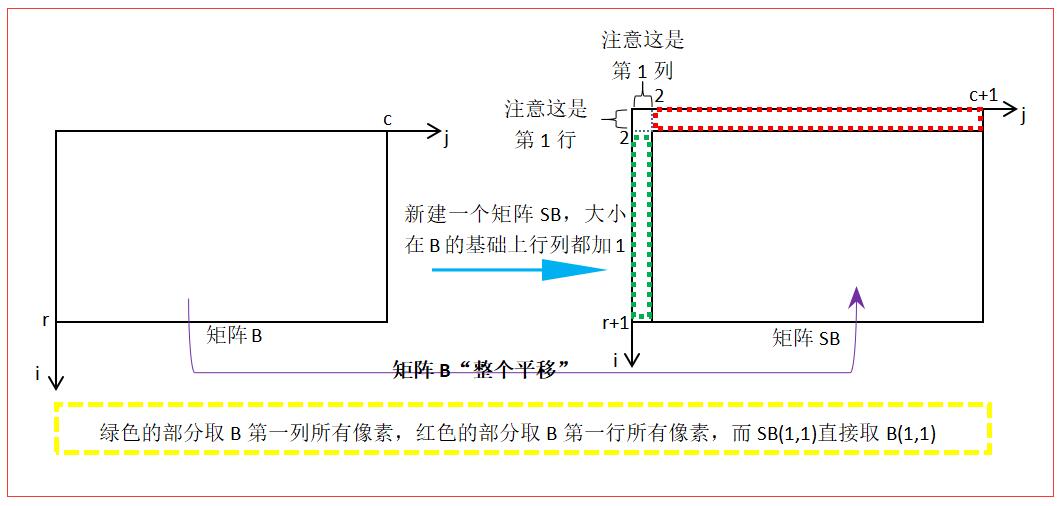
SB = zeros(r+1,c+1);        %Create a new matrixSB，Size inBOn the basis of1
%%%%%handle SB boundary%%%%%
SB(2:r+1,2:c+1)=B;
SB(2:r+1,1)=B(:,1);
SB(1,2:c+1)=B(1,:);
SB(1,1)=B(1,1);
%%%%%handle SB boundary%%%%%
     for Ai=1:nr
        for Aj=1:nc
         Bi=(Ai-1)/S;       %reachAiCorrespondingBiCoordinates,AiByBiZoom firstSTimes, and then move forward in the vertical direction1obtain
         Bj=(Aj-1)/S;       %reachAjCorrespondingBjCoordinates,AjByBjZoom firstSTimes, and then move forward in the horizontal direction1obtain
         i=fix(Bi);         %Round to zero to find the coordinatesBiIntegral part of
         j=fix(Bj);         %Round to zero to find the coordinatesBjInteger part of
         u=Bi-i;            %Find out the coordinatesBiDecimal part of
         v=Bj-j;            %Find out the coordinatesBjDecimal part of
         i=i+1;             %This is in the matrixSBNot in the matrixBThere is translation in the vertical direction, plus1correspondingBOn i value
         j=j+1;             %This is in the matrixSBNot in the matrixBThere is translation in the horizontal direction, plus1correspondingBOn j value
         A(Ai,Aj)=(1-u)*(1-v)*SB(i,j)+u*v*SB(i+1,j+1)+u*(1-v)*SB(i+1,j)+(1-u)*v*SB(i,j+1);%Bilinear interpolation calculationA(Ai,Aj)
        end  
    end
end

Then the function can be called:

clc                                 
I=rgb2gray(imread('cakesk.jpg'));
figure,imshow(I); 
Dst=imscale(I,1.5);        %call imscale()function
figure,imshow(uint8(Dst));
imwrite(Dst,'ims1.5.jpg');  %Store scaled images Dst,The filename is named ims1.5.jpg

The results are as follows: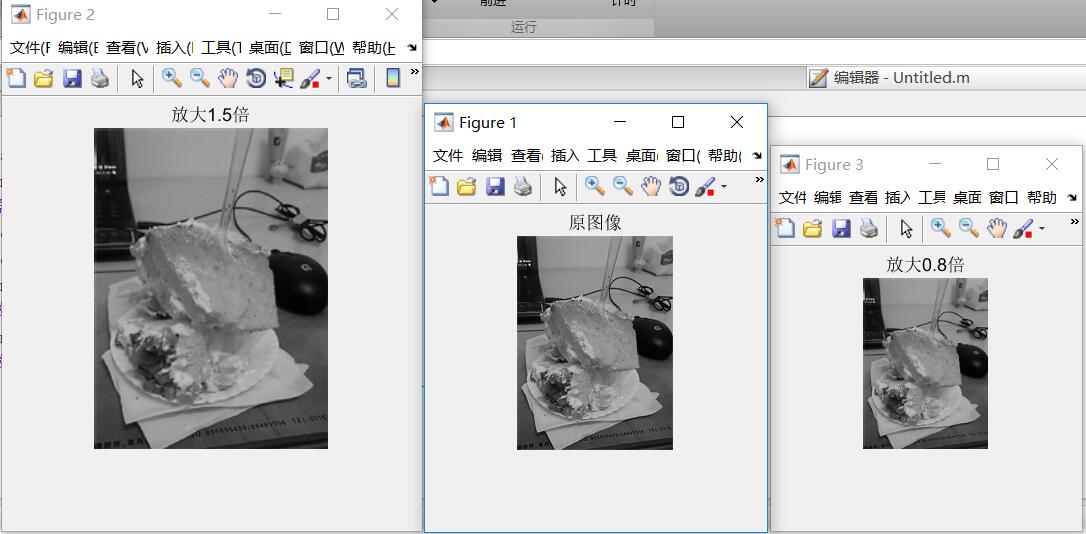

New matrix and matrix boundary operation: