catalogue
2.1 basic concepts of genetic algorithm
2.2 characteristics of genetic algorithm
3.1 source code implementation
3.2 genetic algorithm package sko GA
1 Introduction
Genetic algorithm (GA) is an adaptive global optimization search algorithm formed by simulating the genetic and evolutionary process of organisms in the natural environment. It was first proposed by Professor J.H.Holland of the United States and originated from the research on natural and artificial adaptive systems in the 1960s; In the 1970s, K.A.De Jong carried out a large number of pure numerical function optimization experiments on the computer based on the idea of genetic algorithm. In the 1980s, genetic algorithm was summarized by D.J.Goldberg on the basis of a series of research work. Genetic algorithm is a random global search and optimization method developed by imitating the biological evolution mechanism in nature. It draws lessons from Darwin's theory of evolution and Mendel's genetic theory. In essence, it is a parallel, efficient and global search method. It can automatically obtain and accumulate knowledge about the search space in the search process, and adaptively control the search process to obtain the optimal solution. Genetic algorithm operation: use the principle of "survival of the fittest" to produce an approximate optimal solution in the potential solution population one by one. In each generation, individuals are selected according to their fitness in the problem domain and the reconstruction method borrowed from natural genetics to produce a new approximate solution. This process leads to the evolution of individuals in the population, and the new individuals can adapt to the environment better than the original individuals.
The theory of natural selection holds that the fittest survives. If organisms want to survive, they must fight for survival. Survival struggle includes intraspecific struggle, interspecific struggle and the struggle between organisms and environment. In the struggle for survival, individuals with favorable variation are easy to survive and have more opportunities to pass on favorable variation to future generations; Individuals with unfavorable variation are easy to be eliminated and have much less chance of producing offspring. Therefore, all individuals who win in the struggle for survival are individuals with strong adaptability to the environment. Darwin called this process of survival of the fittest and elimination of the fittest in the struggle for survival natural selection. Darwin's theory of natural selection shows that heredity and variation are the internal factors that determine biological evolution. Heredity refers to the similarity of traits between parents and offspring; Variation refers to the differences in traits between parents and offspring, as well as between individuals of offspring. In organisms, heredity and variation are closely related. The genetic traits of an organism often mutate, and some of the mutated traits can be inherited. Heredity can continuously transmit biological traits to future generations, so it maintains the characteristics of species; Variation can change the characteristics of organisms, so as to adapt to the new environment and continue to develop. All the life activities of organisms have their material basis, so do the inheritance and variation of organisms. According to the research of modern cytology and genetics, the main carrier of genetic material is chromosome, and gene is a fragment with genetic effect. It stores genetic information, can be copied accurately, and can also mutate. Through the replication and crossover of genes, organisms can select and control the inheritance of their traits. At the same time, through gene recombination, gene variation and chromosome structure and number variation, there are rich and colorful variation phenomena. The genetic characteristics of organisms enable the species in the biological world to maintain relative stability; The variation characteristics of organisms make organisms produce new traits, even form new species, and promote the evolution and development of organisms. Gene crossover and mutation may occur in biology during reproduction, which leads to continuous and weak changes in biological characters, provides material conditions and basis for directional selection of external environment, and makes biological evolution possible.
2 Genetic Algorithm
2.1 basic concepts of genetic algorithm
In short, genetic algorithm uses population search technology to represent the population as a set of problem solutions, generate a new generation of population by applying a series of genetic operations such as selection, crossover and mutation to the current population, and gradually make the population evolve to a state containing approximate optimal solutions. Because genetic algorithm is a calculation method formed by the mutual penetration of natural genetics and computer science, some basic terms related to natural evolution are often used in genetic algorithm, and the corresponding relationship of terms is shown in Table 2.1.
| Genetic terminology | Genetic algorithm terminology |
| group | Feasible solution set |
| individual | feasible solution |
| chromosome | Coding of feasible solutions |
| gene | Component of feasible solution coding |
| Gene form | Genetic coding |
| Fitness | Objective function value |
| choice | Select operation |
| overlapping | Cross operation |
| variation | Mutation operation |
2.2 characteristics of genetic algorithm
Genetic algorithm is a parallel, efficient and global search method formed by simulating the process of heredity and evolution of organisms in the natural environment. It mainly has the following characteristics:
(1) Genetic algorithm takes the coding of decision variables as the operation object. This coding method of decision variables makes it possible to use the concepts of chromosome and gene in biology for reference in the process of optimization calculation, imitate the mechanism of biological heredity and evolution in nature, and conveniently apply genetic operators. Especially for some optimization problems with only code concept but no numerical concept or difficult to have numerical concept, the coding processing method shows its unique advantages.
(2) Genetic algorithm directly takes the value of objective function as search information. It only uses the fitness function value transformed from the objective function value to determine the further search direction and search range, without other auxiliary information such as the derivative value of the objective function. In practical applications, many functions cannot or are difficult to derive, or even have no derivative at all. For this kind of objective function optimization and combinatorial optimization problems, genetic algorithm shows its high superiority, because it avoids the obstacle of function derivation.
(3) Genetic algorithm uses the search information of multiple search points at the same time. The search process of genetic algorithm for the optimal solution starts from an initial group composed of many individuals, not from a single individual.
The selection, crossover, mutation and other operations on this group produce a new generation of groups, including a lot of group information. This information can avoid searching some unnecessary points, which is equivalent to searching more points, which is a unique implicit parallelism of genetic algorithm.
(4) Genetic algorithm is a probability based search technology. Genetic algorithm belongs to adaptive probability search technology. Its selection, crossover, mutation and other operations are carried out in a probabilistic way, which increases the flexibility of its search process. Although this probability characteristic will also produce some individuals with low fitness in the population, with the progress of evolution, more excellent individuals will always be born in the new population. Compared with other algorithms, the robustness of genetic algorithm makes the influence of parameters on its search effect as small as possible. (5) Genetic algorithm has the characteristics of self-organization, self-adaptive and self-learning. When genetic algorithm uses the information obtained from the evolutionary process to organize the search by itself, the individuals with high fitness have higher survival probability and obtain the gene structure more suitable for the environment. At the same time, genetic algorithm is scalable and easy to combine with other algorithms to generate a hybrid algorithm combining the advantages of both sides.
2.3 program block diagram
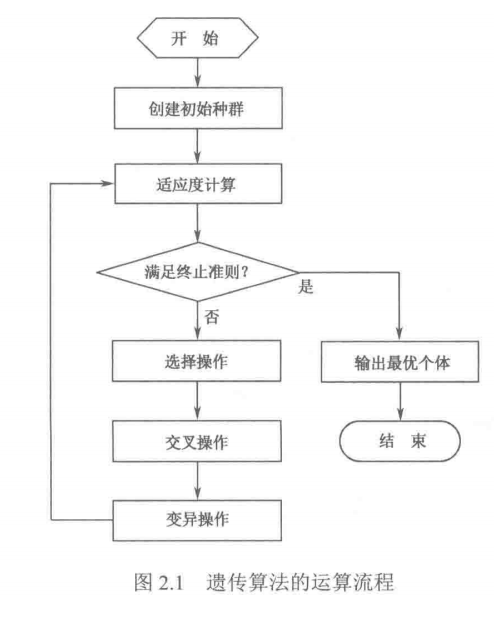
The operation flow of genetic algorithm is shown in Figure 2.1. The specific steps are as follows:
(1) Initialization. Set the evolutionary algebra counter g=0, set the maximum evolutionary algebra G, and randomly generate NP individuals as the initial population P(0).
(2) Individual evaluation. Calculate the fitness of each individual in population P().
(3) Select the operation. The selection operator is applied to the population, and some excellent individuals are selected to inherit to the next generation population according to the individual fitness and certain rules or methods
(4) Cross operation. The crossover operator is applied to the population. For the selected paired individuals, some chromosomes between them are exchanged with a certain probability to produce new individuals.
(5) Mutation. The mutation operator is applied to the population to change one or some gene values to other alleles with a certain probability for the selected individuals. Population P(i) is selected, crossed and mutated to obtain the next generation population P(t+1). The fitness value is calculated and sorted according to the fitness value to prepare for the next genetic operation.
(6) Judgment of termination conditions: if G < g, then g=g+1, go to step (2); If G > G, the individual with the maximum fitness obtained in the evolution process is output as the optimal solution and the calculation is terminated.
3 Python code implementation
3.1 source code implementation
# -*- coding: utf-8 -*-
#========Import related packages============
import numpy as np
import matplotlib.pyplot as plt
#=====Fitness function, get the maximum value======
def fitness(x):
return x + 16 * np.sin(5 * x) + 10 * np.cos(4 * x)
#=====Individual class============
class indivdual:
def __init__(self):
self.x = 0 # Chromosome coding
self.fitness = 0 # Individual fitness value
def __eq__(self, other):
self.x = other.x
self.fitness = other.fitness
#=====Initialize population===========
#pop is the population fitness storage array, and N is the number of individuals
def initPopulation(pop, N):
for i in range(N):
ind = indivdual()#Individual initialization
ind.x = np.random.uniform(-10, 10)# Individual code- The normal distribution of 10 and 10 can set its own limit boundary
ind.fitness = fitness(ind.x)#Calculate individual fitness function value
pop.append(ind)#Add the individual fitness function value to the population fitness array pop
#======Selection process==============
def selection(N):
# Two individuals are randomly selected from the population for variation (Roulette is not used here, but random selection is used directly)
return np.random.choice(N, 2)
#===Combination / crossover process=============
def crossover(parent1, parent2):
child1, child2 = indivdual(), indivdual()#Father, mother
child1.x = 0.9 * parent1.x + 0.1 * parent2.x #Cross 0.9,0.1, other coefficients can be set
child2.x = 0.1 * parent1.x + 0.9 * parent2.x
child1.fitness = fitness(child1.x)#Sub 1 fitness function value
child2.fitness = fitness(child2.x)#Sub 2 fitness function value
return child1, child2
#=====Variation process==========
def mutation(pop):
# Randomly select one from the population for mutation
ind = np.random.choice(pop)
# Mutation by random assignment
ind.x = np.random.uniform(-10, 10)
ind.fitness = fitness(ind.x)
#======Final execution===========
def implement():
#===Number of individuals in population====
N = 40
# population
POP = []
# Number of iterations
iter_N = 400
# Initialize population
initPopulation(POP, N)
#====Evolutionary process======
for it in range(iter_N):#Traverse each generation
a, b = selection(N)#Two individuals were randomly selected
if np.random.random() < 0.65: # Cross bonding with a probability of 0.65
child1, child2 = crossover(POP[a], POP[b])
new = sorted([POP[a], POP[b], child1, child2], key=lambda ind: ind.fitness, reverse=True)#Compare parents and offspring and keep the best two
POP[a], POP[b] = new[0], new[1]
if np.random.random() < 0.1: # Variation with a probability of 0.1
mutation(POP)
POP.sort(key=lambda ind: ind.fitness, reverse=True)
return POP
if __name__ =='__main__':
POP = implement()
#=======Drawing code============
def func(x):
return x + 16 * np.sin(5 * x) + 10 * np.cos(4 * x)
x = np.linspace(-10, 10, 100000)
y = func(x)
scatter_x = np.array([ind.x for ind in POP])
scatter_y = np.array([ind.fitness for ind in POP])
best=sorted(POP,key=lambda POP:POP.fitness,reverse=True)[0]#Best point
print('best_x',best.x)
print('best_y',best.fitness)
plt.plot(x, y)
#plt.scatter(scatter_x, scatter_y, c='r')
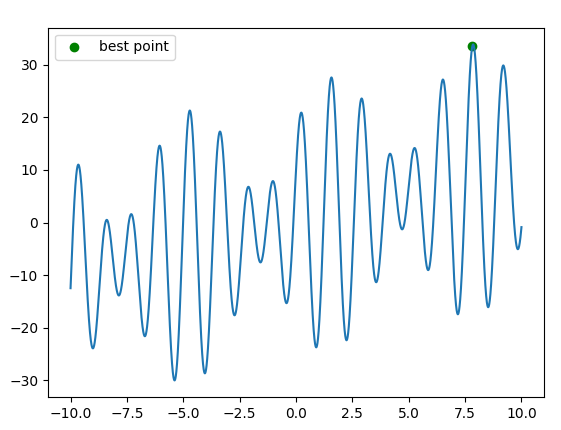
plt.scatter(best.x,best.fitness,c='g',label='best point')
plt.legend()
plt.show()
Results:
best_x 7.821235839598371 best_y 33.52159669619314
3.2 genetic algorithm package sko GA
3.2.1 case 1
#=======Import related libraries=========
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sko.GA import GA
#=====Objective function========
def fun(p):
#The function has a large number of local minima and a global minimum at (0,0) where the strong impact value is 0
#GA requires the input of dimension 2 and above, so I pass in two parameters X1 and x2
x1, x2 = p
x = np.square(x1) + np.square(x2)
return 0.5 + (np.square(np.sin(x)) - 0.5) / np.square(1 + 0.001 * x)
#=====Call genetic algorithm toolbox========
ga = GA(func=fun, n_dim=2, size_pop=50, max_iter=800, prob_mut=0.001, lb=[-1, -1], ub=[1, 1], precision=1e-7)
best_x, best_y = ga.run()
print('best_x:', best_x, '\n', 'best_y:', best_y)
#========Visualization===============
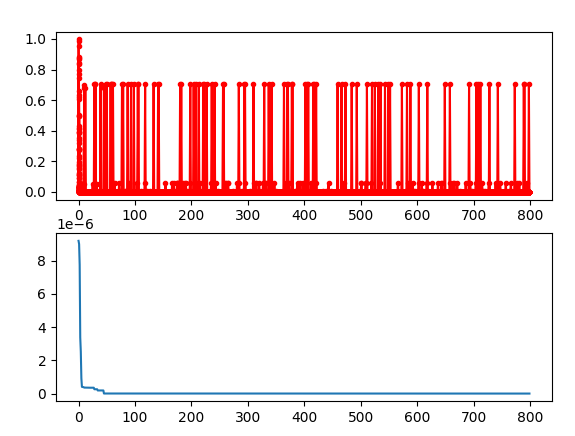
Y_history = pd.DataFrame(ga.all_history_Y)
fig, ax = plt.subplots(2, 1)
ax[0].plot(Y_history.index, Y_history.values, marker='.', color='red')
Y_history.min(axis=1).cummin().plot(kind='line')
plt.show()Results:
best_x: [-2.98023233e-08 8.94069698e-08] best_y: [0.]
3.2.2 case 2
Compare with source code:
#======Import related packages=========
import numpy as np
import matplotlib.pyplot as plt
from sko.GA import GA #Genetic algorithm Toolkit
#=========Fitness function, get the maximum value=========
#Because the GA function is to find the minimum value, I add a negative sign to the fitness function
#GA requires the input of dimension 2 and above, so I input two parameters, and the second dimension x2 is not used
def fitness(x):
x1, x2 = x
#x1=x
return -(x1 + 16 * np.sin(5 * x1) + 10 * np.cos(4 * x1))
#==========Application of genetic algorithm package==================
ga = GA(func=fitness, n_dim=2, size_pop=50, max_iter=800, lb=[-10,0], ub=[10,0],precision=1e-7)
best_x, best_y = ga.run()
print('best_x:', best_x[0], '\n', 'best_y:', -best_y)
#==========Visualization================
def func(x):
return x + 16 * np.sin(5 * x) + 10 * np.cos(4 * x)
x = np.linspace(-10, 10, 100000)
y = func(x)
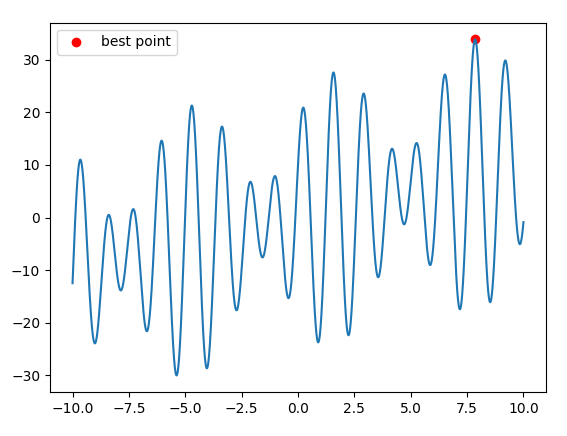
plt.plot(x, y)
plt.scatter(best_x[0], -best_y, c='r',label='best point')
plt.legend()
plt.show()
best_x: 7.855767376183596 best_y: [33.8548745]
4 reference
--------
https://blog.csdn.net/kobeyu652453/article/details/109527260