RRT algorithm, also known as fast random expansion number algorithm, is a universal path planning algorithm. Why it is a universal algorithm, because it is highly possible to find a path under any harsh conditions.
However, such algorithms often have disadvantages:
1. Every iteration is to find points randomly, which leads to the fact that the iteration time depends largely on luck
2. Due to the strong randomness of this algorithm, it is difficult to find a path quickly in a very simple obstacle avoidance environment
In this paper, the initial RRT algorithm (without any improvement of the algorithm) is simulated in code. It is intended to find a path under the condition of multiple obstacles. The algorithm itself does not involve optimization, so there is no optimization for the found path.
RRT algorithm model is explained in detail on the Internet and is very easy to understand. It is not repeated here, but only part of the code implementation is given. This is some of my own opinions on RRT algorithm, maybe some simple, just hope to give you more or less help, don't spray if you don't like it.
Code introduction:
In a space full of cuboid and cylinder obstacles, arbitrary points are given as target points for path planning
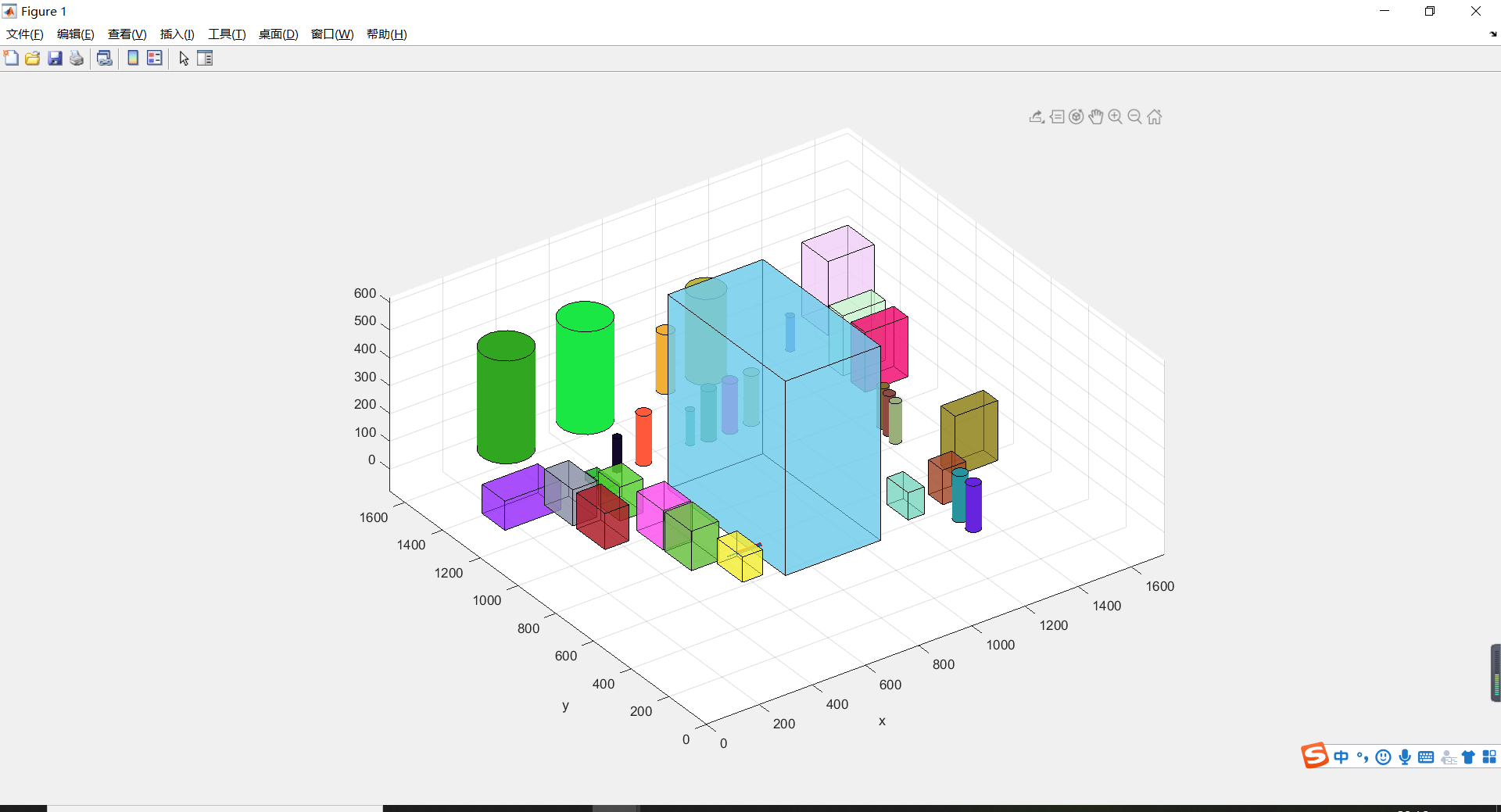
After the iteration, the path found is shown by the red line in the following part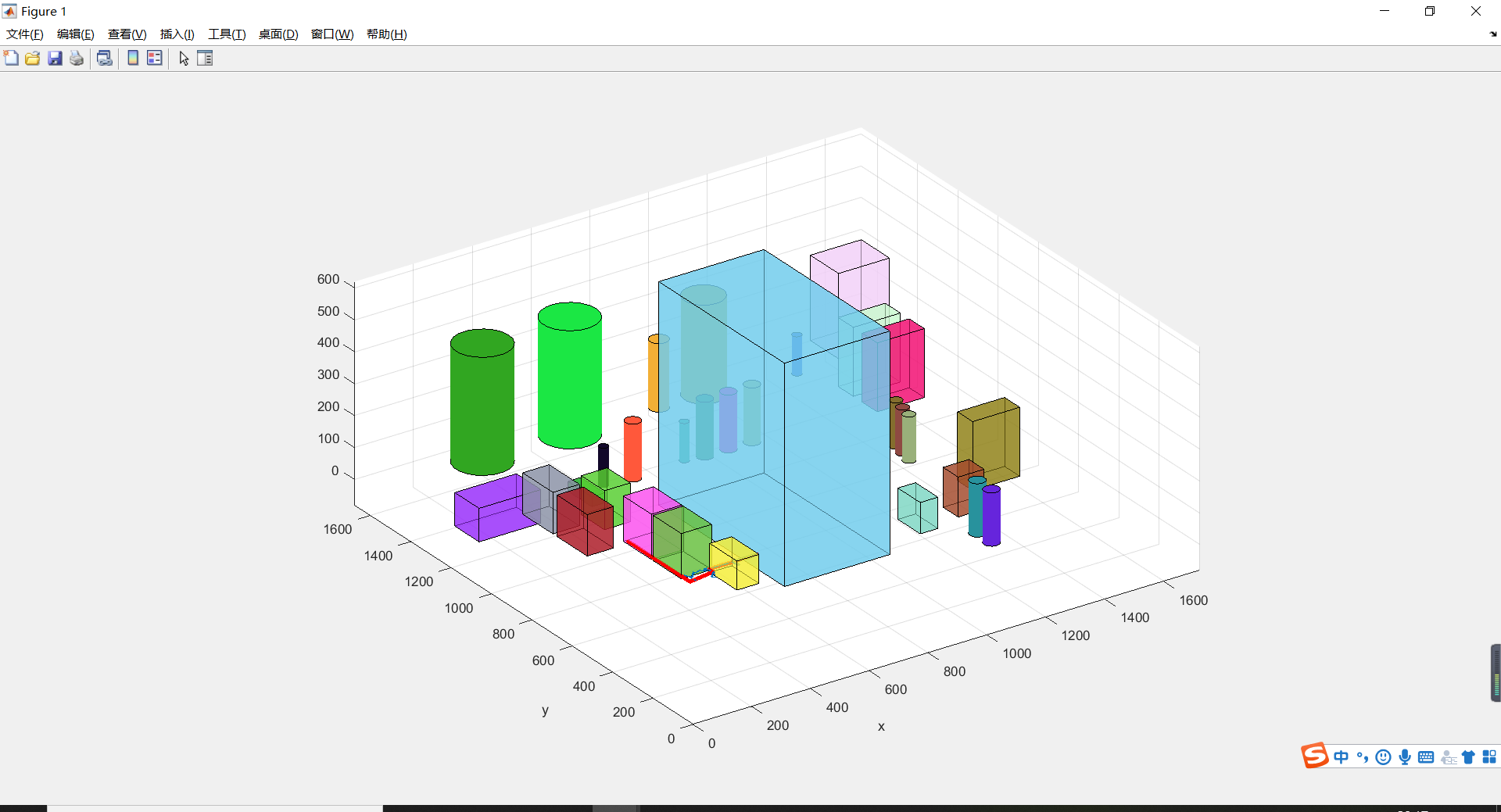
Code part:
Main function, file named rrtmain m
%% Empty variable
clear
clc
%% Import data
[dat_chicun,dat_jiaodian,dat_xia] = xlsData();
%% Drawing
color_mat=rand(size(dat_jiaodian,1),3); %Generate random matrix as color
hold on %Draw on the same image
grid on % Draw grid
for k1=1:size(dat_jiaodian,1)
plotcube(dat_chicun(k1,[2,1,3]),dat_jiaodian(k1,1:3),0.6,color_mat(k1,:))%This is a function of drawing a cuboid obstacle
end
for k2=1:size(dat_xia,1)
plot_cylinder(dat_xia(k2,1:3),dat_xia(k2,4),dat_xia(k2,5),1,rand(1,3));%This is a function of drawing a cylindrical obstacle
end
axis([0 2000 0 2000 -200 600 ]) %Set the visualization range of the image
axis equal % The visual intervals of image axes are equal
xlabel('x');
ylabel('y')
%% Data reprocessing
num_cube = size(dat_jiaodian(2:end,:),1); %Number of cuboid obstacles 15
[dat_cube,dat_pingban] = cube_coor_deal(dat_jiaodian); %The corner elements of the box are stored in the cell array for easy indexing
num_cylinder = size(dat_xia,1); %Number of cylindrical obstacles
dat_cylinder = cylinder_coor_deal(dat_xia); %The cylinder data is stored in the cell array for easy access
% num_cube: Number of cuboid obstacles
% dat_cube: Cell array of box corners
% dat_pingban: Plate corner cell array
% num_cylinder: Number of cylindrical obstacles
% dat_cylinder: Cylindrical obstacle data cell
%% rrt Algorithm part
GG = [704 700 -30;612 700 -30;537 680 -30;447 980 -30];%Target point coordinates. If there are multiple target points, put the coordinates of each target point here
PATH = [];
for k3 = 1:size(GG,1)-1
start = GG(k3,:);
goal = GG(k3+1,:);
path_best = RRT(num_cube,dat_cube,num_cylinder,dat_cylinder,start,goal);%Every time the best path is found, it is stored in this variable
%Note: this path point is processed through redundant points, so there are few points
% line(path_best(:,1),path_best(:,2),path_best(:,3),'LineWidth',2,'Color','b');%Draw the set of points to find the path with a straight line
PATH = [PATH;path_best];
endfunction dist = calculate_distance3(mat_start,mat_goal) %% This function calculates the distance of 3D points dist = sqrt((mat_start(1)-mat_goal(1))^2+(mat_start(2)-mat_goal(2))^2+(mat_start(3)-mat_goal(3))^2);
function flag = collision_checking_cube(num_cube,dat_cube,coor_new,coor_near,Delta,deta)
%Return 1 in case of collision
flag = 0;
% flag1 = 0;
% flag2 = 0;
% flag2_mid1 = 0;
% flag2_mid2 = 0;
% flag2_mid3 = 0;
for k1=1:num_cube
x_min = min(dat_cube{k1}(:,1));
x_max = max(dat_cube{k1}(:,1));
y_min = min(dat_cube{k1}(:,2));
y_max = max(dat_cube{k1}(:,2));
z_min = min(dat_cube{k1}(:,3));
z_max = max(dat_cube{k1}(:,3));
for r=0:Delta/deta:Delta
coor_mid = rrt_steer(coor_new,coor_near,r);
if ((x_min<coor_mid(1))&&(coor_mid(1)<x_max))&&((y_min<coor_mid(2))&&(coor_mid(2)<y_max))&&((z_min<coor_mid(3))&&(coor_mid(3)<z_max))
flag = 1;
break;
end
end
end
function flag = collision_checking_cylinder(num_cylinder,dat_cylinder,coor_new,coor_near,Delta,deta)
%Return 1 in case of collision
flag = 0;
for k1=1:num_cylinder
x_coor = dat_cylinder{k1}(1);
y_coor = dat_cylinder{k1}(2);
z_coor = dat_cylinder{k1}(3);
R = dat_cylinder{k1}(4)/2;
height = dat_cylinder{k1}(5);
for r=Delta/deta:Delta
coor_mid = rrt_steer(coor_new,coor_near,r);
if (((x_coor-coor_mid(1))^2+(y_coor-coor_mid(2))^2-R^2) < 0) && (z_coor<coor_mid(3)) && (coor_mid(3)<z_coor+height)
flag = 1;
break;
end
end
endfunction [dat_cube,dat_pingban] = cube_coor_deal(dat_jiaodian)
%% Store 15 obstacle corners in 15 cell arrays
mid1 = dat_jiaodian(1:end,:);
lin = size(mid1,1);
col = size(mid1,2);
mid3 = zeros(col/3,3);
dat_cube_mid = cell(lin,1);
for k1=1:lin
for k2=1:col/3
mid2 = mid1(k1,3*(k2-1)+1:3*(k2-1)+3);
mid3(k2,:) = mid2;
end
dat_cube_mid{k1}(:,:) = mid3;
end
dat_cube = dat_cube_mid;
dat_cube(1,:)=[];
dat_pingban{1} = dat_cube_mid{1};function dat_cylinder = cylinder_coor_deal(dat_xia)
%% The diameter and height of 16 cylindrical obstacles are put in the cell array. As for why they exist in the cell array, there is no why, personal preference
lin = size(dat_xia,1);
dat_cylinder=cell(lin,1);
for k1=1:lin
dat_cylinder{k1}=dat_xia(k1,:);
endfunction path_best = delete_redundant_points(path,num_cylinder,dat_cylinder,num_cube,dat_cube)
num_points = size(path,1);
count = 1;
start_point = path(1,:);
index = zeros(1,num_points);
for k1 = 1:num_points-2
count = count+1;
final_point = path(count+1,:);
if (collision_checking_cylinder(num_cylinder,dat_cylinder,final_point,start_point,calculate_distance3(final_point,start_point),3)||...
collision_checking_cube(num_cube,dat_cube,final_point,start_point,calculate_distance3(final_point,start_point),3))
start_point = path(count,:);
else
index(count) = count;
end
end
index(index==0) = [];
path([index(end:-1:1)],:) = [];
path_best = path;
function plot_cylinder(coor,diameter,height,facealpha,color)
%% plot_cylinder(dat_xia(k2,1:3),dat_xia(k2,4),dat_xia(k2,5),1,rand(1,3));
% The first parameter is the coordinate value of the bottom center of the cylinder, the second parameter is the cylinder diameter, and the third parameter is the cylinder height
% The fourth parameter is transparency and the fifth parameter is color matrix
%% Function explanation: treat this function as a black box. You only need to remember the input of the function to know what it is for and what is inside
%% The implementation is too complex to explain clearly
% coor: Central coordinates
% diameter: diameter
% height: height
% facealpha: transparency
% color: colour
r = diameter/2;
theta = 0:0.3:pi*2;
hold on
for k1 = 1:length(theta)-1
X=[coor(1)+r*cos(theta(k1)) coor(1)+r*cos(theta(k1+1)) coor(1)+r*cos(theta(k1+1)) coor(1)+r*cos(theta(k1))];
Y=[coor(2)+r*sin(theta(k1)) coor(2)+r*sin(theta(k1+1)) coor(2)+r*sin(theta(k1+1)) coor(2)+r*sin(theta(k1))];
Z=[coor(3),coor(3),coor(3)+height,coor(3)+height];
h=fill3(X,Y,Z,color);
set(h,'edgealpha',0,'facealpha',facealpha)
end
X=[coor(1)+r*cos(theta(end)) coor(1)+r*cos(theta(1)) coor(1)+r*cos(theta(1)) coor(1)+r*cos(theta(end))];
Y=[coor(2)+r*sin(theta(end)) coor(2)+r*sin(theta(1)) coor(2)+r*sin(theta(1)) coor(2)+r*sin(theta(end))];
Z=[coor(3),coor(3),coor(3)+height,coor(3)+height];
h=fill3(X,Y,Z,color);
set(h,'edgealpha',0,'facealpha',facealpha)
fill3(coor(1)+r*cos(theta),coor(2)+r*sin(theta),coor(3)*ones(1,size(theta,2)),color)
fill3(coor(1)+r*cos(theta),coor(2)+r*sin(theta),height+coor(3)*ones(1,size(theta,2)),color)
view(3)function plotcube(varargin)
%% plotcube(dat_chicun(k1,[2,1,3]),dat_jiaodian(k1,1:3),0.6,color_mat(k1,:))
%% The first parameter is the length, width and height value of each box, the second parameter is the first coordinate value of the corner, and the third parameter is transparency with a range of 0-1.
%% The fourth parameter is the color matrix[a,b,c] abc Each value range is 0-1
%%
inArgs = { ...
[10 56 100] , ... % Default edge sizes (x,y and z)
[10 10 10] , ... % Default coordinates of the origin point of the cube
.7 , ... % Default alpha value for the cube's faces
[1 0 0] ... % Default Color for the cube
};
inArgs(1:nargin) = varargin;
[edges,origin,alpha,clr] = deal(inArgs{:});
XYZ = { ...
[0 0 0 0] [0 0 1 1] [0 1 1 0] ; ...
[1 1 1 1] [0 0 1 1] [0 1 1 0] ; ...
[0 1 1 0] [0 0 0 0] [0 0 1 1] ; ...
[0 1 1 0] [1 1 1 1] [0 0 1 1] ; ...
[0 1 1 0] [0 0 1 1] [0 0 0 0] ; ...
[0 1 1 0] [0 0 1 1] [1 1 1 1] ...
};
XYZ = mat2cell(...
cellfun( @(x,y,z) x*y+z , ...
XYZ , ...
repmat(mat2cell(edges,1,[1 1 1]),6,1) , ...
repmat(mat2cell(origin,1,[1 1 1]),6,1) , ...
'UniformOutput',false), ...
6,[1 1 1]);
cellfun(@patch,XYZ{1},XYZ{2},XYZ{3},...
repmat({clr},6,1),...
repmat({'FaceAlpha'},6,1),...
repmat({alpha},6,1)...
);
view(3);function path_best = RRT(num_cube,dat_cube,num_cylinder,dat_cylinder,start,goal)
%% Process initialization
Delta=2; % Set the expansion step size and the maximum distance allowed by the expansion node. The larger the data, the faster the iteration, but the worse the effect than the optimal solution
max_iter = 10000; % The maximum number of iterations. If the path is not found after this number, it is considered that the path cannot be found
Map = [goal(1)-start(1),goal(2)-start(2),goal(3)-start(3)];
count = 1;
%% Build initialization tree
T.x(1) = start(1);
T.y(1) = start(2);
T.z(1) = start(3);
T.xpar(1) = goal(1);
T.ypar(1) = goal(2);
T.zpar(1) = goal(3);
T.dist(1) = 0;
T.indpre(1) = 0;
tic
for iter = 1:max_iter
% step1: Random sampling on map
coor_rand = rrt_sample(Map,goal,start); %Random sampling in space, coor_rand It's a 1×3 Array of
% plot3(coor_rand(1),coor_rand(2),coor_rand(3),'r*')
% step2 : Traverse the tree to find the nearest parent node
[coor_near,coor_index] = rrt_near(coor_rand,T);
% step3: Expand to get new nodes
coor_new = rrt_steer(coor_rand,coor_near,Delta);
% step4: collision detection ,In case of collision, 1 will be returned
flag1 = collision_checking_cube(num_cube,dat_cube,coor_new,coor_near,Delta,3);%This part is a function to detect whether it collides with a box obstacle
flag2 = collision_checking_cylinder(num_cylinder,dat_cylinder,coor_new,coor_near,Delta,3);%This part is the parameter to detect whether it collides with the cylinder obstacle
if flag1 || flag2
continue;
end
count = count+1;
% step5:Insert new point
T.x(count) = coor_new(1);
T.y(count) = coor_new(2);
T.z(count) = coor_new(3);
T.xpar(count) = coor_near(1);
T.ypar(count) = coor_near(2);
T.zpar(count) = coor_near(3);
T.dist(count) = calculate_distance3(coor_new,coor_near);
T.indpre(count) = coor_index;
line([coor_near(1),coor_new(1)],[coor_near(2),coor_new(2)],[coor_near(3),coor_new(3)],'LineWidth',1);
pause(0.1); %Pause 0.1s,bring RRT The expansion process is easy to observe;
% be careful: pause Pause the function when the function is used. This part is very important if it is used to display animation. However, if it is not added, the animation will be still and the moving picture cannot be displayed
% step6:After each iteration, check whether it can be directly connected to the end point
if ~(collision_checking_cylinder(num_cylinder,dat_cylinder,goal,coor_new,calculate_distance3(goal,coor_new),20)||...
collision_checking_cube(num_cube,dat_cube,goal,coor_new,calculate_distance3(goal,coor_new),20))
count = count+1;
T.x(count) = goal(1);
T.y(count) = goal(2);
T.z(count) = goal(3);
T.xpar(count) = coor_new(1);
T.ypar(count) = coor_new(2);
T.zpar(count) = coor_new(3);
T.dist(count) = calculate_distance3(coor_new,goal);
T.indpre(count) = 0;
line([goal(1),coor_new(1)],[goal(2),coor_new(2)],[goal(3),coor_new(3)],'LineWidth',3,'MarkerSize',2);
pause(0.1); %Pause 0.1s,bring RRT The expansion process is easy to observe
break;
end
end
toc
% After finding the path point, the algorithm finds the parent point set that reaches the destination and stores it in the path Variable
if iter>max_iter
error('Path planning fails when the maximum number of iterations is exceeded');
end
path(1,1) = T.x(end);path(1,2) = T.y(end);path(1,3) = T.z(end);
path(2,1) = T.x(end-1);path(2,2) = T.y(end-1);path(2,3) = T.z(end-1);
count2 = 2;
ind_pre = T.indpre(end-1);
if iter<=max_iter
while ~(ind_pre==0)
count2 = count2+1;
path(count2,1) = T.x(ind_pre);
path(count2,2) = T.y(ind_pre);
path(count2,3) = T.z(ind_pre);
ind_pre = T.indpre(ind_pre);
end
end
% line(path(:,1),path(:,2),path(:,3),'LineWidth',1,'Color','r');
%% RRT The algorithm finds all sets of new points, and then removes redundant points
path_best = delete_redundant_points(path,num_cylinder,dat_cylinder,num_cube,dat_cube);
line(path_best(:,1),path_best(:,2),path_best(:,3),'LineWidth',3,'Color','r');
function [coor_near,coor_index] = rrt_near(coor_rand,T)
min_distance = calculate_distance3(coor_rand,[T.x(1),T.y(1),T.z(1)]);
for T_iter=1:size(T.x,2)
temp_distance=calculate_distance3(coor_rand,[T.x(T_iter),T.y(T_iter),T.z(T_iter)]);
if temp_distance<=min_distance
min_distance=temp_distance;
coor_near(1)=T.x(T_iter);
coor_near(2)=T.y(T_iter);
coor_near(3)=T.z(T_iter);
coor_index=T_iter;
end
end
function coor_rand = rrt_sample(Map,goal,start) rat = 1.5; if unifrnd(0,1)<0.5 coor_rand(1)= unifrnd(-0.2,rat)* Map(1); coor_rand(2)= unifrnd(-0.2,rat)* Map(2); coor_rand(3)= unifrnd(-0.2,rat)* Map(3); coor_rand = coor_rand+start; else coor_rand=goal; end
function coor_new = rrt_steer(coor_rand,coor_near,Delta) deltaX = coor_rand(1)-coor_near(1); deltaY = coor_rand(2)-coor_near(2); deltaZ = coor_rand(3)-coor_near(3); r = sqrt(deltaX^2+deltaY^2+deltaZ^2); fai = atan2(deltaY,deltaX); theta = acos(deltaZ/r); R = Delta; x1 = R*sin(theta)*cos(fai); x2 = R*sin(theta)*sin(fai); x3 = R*cos(theta); coor_new(1) = coor_near(1)+x1; coor_new(2) = coor_near(2)+x2; coor_new(3) = coor_near(3)+x3; end
function PATH = smooth_deal(PATH) hold on; x = PATH(:,1)'; y = PATH(:,2)'; z = PATH(:,3)'; %Cubic spline interpolation t1=1:1:size(PATH,1); t=1:0.5:size(PATH,1); XX=spline(t1,x,t); YY=spline(t1,y,t); ZZ=spline(t1,z,t); plot3(XX,YY,ZZ,'r-') view(3)
function [dat_chicun,dat_jiaodian,dat_xia] = xlsData()
%% Fifteen cuboid obstacles are wide, long and high. The first row is not, and the first row is the floor. They are not used as obstacles
dat_chicun = [0.1, 0.1, 0.1;
624, 358, 700;
140, 173, 267;
121, 210, 105;
150, 90, 130;
150, 90, 130;
115, 88, 122;
140, 103, 142;
140, 103, 142;
135, 75, 91;
75, 160, 216;
75, 160, 216;
111, 60, 98;
118, 44, 31;
75, 160, 216;
75, 88, 125];
%% Corner coordinates of fifteen cuboid obstacles, the first row is not
dat_jiaodian = [0,0,0,0,0,1,1767,0,1,1767,0,0,1767,1679,0,1767,1679,1,0,1679,0,0,1679,1;
704,573,-80,704,573,620,1062,573,620,1062,573,-80,1062,1197,-80,1062,1197,620,704,1197,-80,704,1197,620;
1550,1539,1,1550,1539,268,1723,1539,268,1723,1539,1,1723,1679,1,1723,1679,268,1550,1679,1,1550,1679,268;
150,1280,-74,150,1280,31,360,1280,31,360,1280,-74,360,1401,-74,360,1401,31,150,1401,-74,150,1401,31;
264,1080,1,264,1080,131,354,1080,131,354,1080,1,354,1230,1,354,1230,131,264,1230,1,264,1230,131;
264,910,1,264,910,131,354,910,131,354,910,1,354,1060,1,354,1060,131,264,1060,1,264,1060,131;
398,1020,1,398,1020,123,486,1020,123,486,1020,1,486,1135,1,486,1135,123,398,1135,1,398,1135,123;
447,858,-40,447,858,102,550,858,102,550,858,-40,550,998,-40,550,998,102,447,998,-40,447,998,102;
447,710,-40,447,710,102,550,710,102,550,710,-40,550,850,-40,550,850,102,447,850,-40,447,850,102;
537,565,-41,537,565,50,612,565,50,612,565,-41,612,700,-41,612,700,50,537,700,-41,537,700,50;
1450,1320,1,1450,1320,217,1610,1320,217,1610,1320,1,1610,1395,1,1610,1395,217,1450,1395,1,1450,1395,217;
1450,1201,1,1450,1201,217,1610,1201,217,1610,1201,1,1610,1276,1,1610,1276,217,1450,1276,1,1450,1276,217;
1170,579,-48,1170,579,50,1230,579,50,1230,579,-48,1230,690,-48,1230,690,50,1170,690,-48,1170,690,50;
451,1160,1,451,1160,32,495,1160,32,495,1160,1,495,1278,1,495,1278,32,451,1278,1,451,1278,32;
1390,640,1,1390,640,217,1550,640,217,1550,640,1,1550,715,1,1550,715,217,1390,715,1,1390,715,217;
1262,525,1,1262,525,126,1350,525,126,1350,525,1,1350,600,1,1350,600,126,1262,600,1,1262,600,126];
%% The first three columns are the coordinates of the center of the circle at the bottom of sixteen cylindrical obstacles, the fourth column is the diameter, and the fifth column is the height
dat_xia = [ 952,1330,-51,50,181;
1032,1330,-51,50,181;
1112,1330,-51,50,181;
1430,1079,-51,40,145;
1420,1032,-51,40,145;
1410,985,-51,40,145;
882,1330,-45,30,123;
707,1330,-51,50,181;
607,1330,-45,30,123;
1450,1600,-43,30,123;
1310,500,-53,50,167;
1310,430,-53,50,167;
1112,1570,1,130,310;
960,1570,1,60,215;
360,1570,1,180,370;
657,1570,1,180,370];
Summary:
The code may be a little long, but it's much cleaner to divide it into multiple sub functions. Specific operation steps: copy each code into a new script file. Except that the main function is named arbitrarily, other script files are named function names. The specific form is as follows.
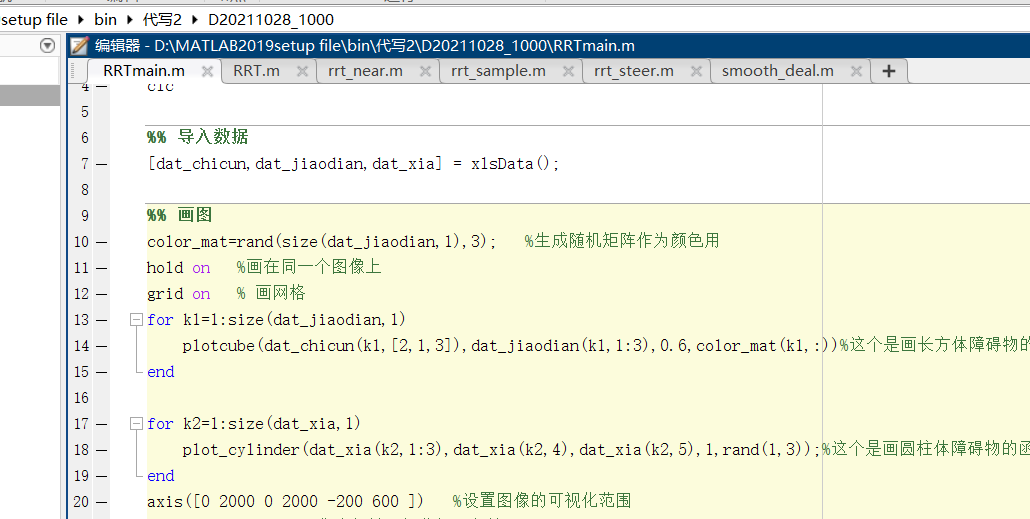
Each sub function has comments, and corresponding comments are added to the main function. I hope it can be helpful to you. Thank you for your support~