Bees collect honey
Bees in nature can always find high-quality honey sources with high efficiency in any environment, and can adapt to environmental changes. The honey collection system of honeybee colony consists of three parts: honey source, hired bee and non hired bee. The advantages and disadvantages of one honey source have many elements, such as the amount of nectar, the distance from the honeybee hive, the difficulty of extraction, etc; Hire bees to contact specific honey sources and tell their companions the information of honey sources in the form of a certain probability; The duty of non employed bees is to find the honey source to be mined, which is divided into following bees and reconnaissance bees. The following peak is to wait in the hive, and the reconnaissance bees are to detect the new honey source around the hive. When bees collect honey, some bees in the hive, as reconnaissance bees, constantly and randomly look for honey sources near the hive. If a honey source with nectar exceeding a certain threshold is found, the reconnaissance bee becomes a hired bee to start collecting honey. After collecting honey, they fly back to the hive and dance a swing dance to inform the following peak. Swing dance is a basic form of information exchange between bees. It conveys important information about the honey source around the hive, such as the direction of the honey source and the distance from the hive. The following peak uses this information to accurately evaluate the quality of the honey source around the hive. When the hired bees finish the swing dance, they return to the original honey source together with some follower bees in the hive to collect honey. The number of follower bees depends on the quality of the honey source. In this way, the bee colony can quickly and effectively find the honey source with the highest amount of nectar.
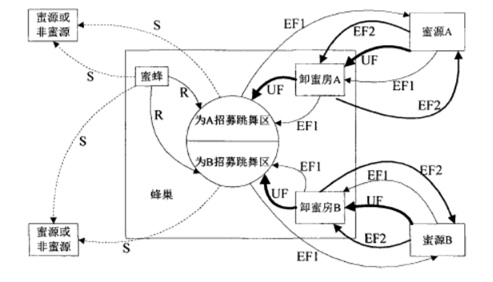
The swarm intelligence of bee collecting honey is realized through the communication, transformation and cooperation between different roles. The specific honey collection process is shown in the figure. At the initial stage, bees appear in the form of reconnaissance bees, and they do not have any understanding of the honey source around the honeycomb. Due to the different internal motivation and external conditions of bees, reconnaissance bees have two choices: ① become a hired bee, start randomly searching for the honey source around the honeycomb, as shown in the figure, ② become a follow peak, and start searching for the honey source after observing the swing dance, as shown in the figure. Suppose two honey sources and are found. After discovering the honey source, the reconnaissance bee becomes a hired bee. The hired bee uses its own attributes to remember the location of the honey source and immediately puts it into honey collection. After collecting honey, the bee returns to the hive with a full load of nectar and unloads the nectar to the honey unloading room. After unloading, the employed bee has three possible behaviors: ① give up the nectar source with a low amount of nectar found by itself and become an unrestricted non employed bee, as shown in the route in the figure; ② In
The recruitment area will dance a swing dance, recruit some people to stay in the hive and follow the peak, and lead them to return to the discovered honey source again, as shown in the route in the figure; ③ Do not recruit other bees, continue to return to the original honey source to collect honey, as shown in the route in the figure. In real life, not all bees collect honey immediately at the beginning. In addition, most bees choose to go back to the recruitment area and dance swing dance to recruit more bees to collect honey.
Algorithm model
Artificial bee colony algorithm is a new intelligent optimization algorithm proposed to simulate the honey collection process of bees. It is also composed of food source, employed bees and non employed bees.
Food source: the food source is the honey source. In any optimization problem, the feasible solution of the problem is given in a certain form. In the artificial bee colony algorithm, the food source is the feasible solution of the optimization problem to be solved, and it is the basic object to be processed in the artificial bee colony algorithm. The quality of the food source can be solved. The quality is evaluated by the amount of nectar in the nectar source, that is, the fitness.
Hired bee: hired bee is the leading bee, which corresponds to the position of food source, and one food source corresponds to one leading bee. In the artificial bee colony algorithm, the number of food sources is equal to the number of leading bees; The task of leading bees is to find food source information and share it with the following bees with a certain probability; The calculation of probability is the selection strategy in artificial bee colony algorithm, which is generally calculated by roulette according to the fitness value.
Non employed bees: non employed bees include following bees and investigation bees. The following bees choose food sources according to the honey source information provided by the leading bees in the recruitment area of the hive, and the investigation bees look for new food sources near the hive. In the artificial bee colony algorithm, the following bee searches for a new food source near the food source according to the information transmitted by the leading bee, and makes greedy selection. If a food source has not been updated after times, the leading bee will become a detection bee, and the detection bee will look for a new food source to replace the original food source.
Algorithm search process
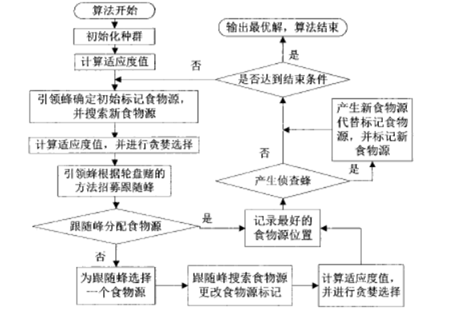In the artificial bee colony algorithm, the artificial bee colony is divided into three types: leading bee, following bee and investigating bee. In each search process, the leading bee and following bee successively mine the food source, that is, look for the optimal solution, while the investigating bee is to observe whether it falls into the local optimal. If it falls into the local optimal, it will randomly search for other possible food sources. Each food source represents a possible solution to the problem, and the nectar amount of the food source corresponds to the quality of the corresponding solution (fitness value fiti).
1, In the search process of artificial bee colony algorithm, initialization is required first, including determining the population number, the maximum number of iterations, MCN, control parameter limit and determining the search space, that is, the range of solutions. The initial solutions xi(i=1,2,3,..., SN) are randomly generated in the search space. SN is the number of food sources. Each solution xi is a d-dimensional vector and D is the dimension of the problem. After initialization, the whole population will repeat the search process of leading bee, following bee and reconnaissance bee until the maximum number of iterations MCN or allowable error value is reached ε.
2, At the beginning of the search process, each leading bee generates a new solution, that is, a new food source, from formula (2-3),
vij=xij+Φij(xij-xkj) (2-3)
Where, k ∈ 1,2, Sn}, j ∈ {1,2,...,D}, and k ≠ i; Φ ij is a random number between [- 1,1]. Calculate the fiti of the new solution and evaluate it. If the fiti of the new solution is better than the old solution, lead the bee to remember the new solution and forget the old solution. On the contrary, it will retain the old solution.
3, After all the leading bees complete the search process, the leading bees will dance a swing dance in the recruitment area and share the solution information and information with the following bees. The following bee calculates the selection probability of each solution according to the formula,
pi=fiti/∑k=1SNfitk. (2-4)
Then, a number is randomly generated in the interval [- 1,1]. If the probability value of the solution is greater than the random number, the following bee generates a new solution from equation (2-3) and tests the fiti of the new solution. If the fiti of the new solution is better than the previous one, the following bee will remember the new solution and forget the old solution; On the contrary, it will retain the old solution.
4, After all the following bees complete the search process, if a solution has not been further updated after limit cycles, it is considered that the solution falls into local optimization, and the food source will be abandoned. If the food source xi is discarded, the leading bee corresponding to this food source will be transformed into a reconnaissance bee. The Scout bee is replaced by a new food source generated by formula (2-5).
xij=xminj+rand(0,1)(xmaxj-xminj) (2-5)
Where j ∈ {1,2..., D}. Then return to the search process and start repeating the cycle.
5, The food source quality of artificial bee colony algorithm is generally the greater the better, that is, the greater the fitness value, the better. Corresponding to the problem to be optimized, it needs to be considered in two cases: minimum problem and maximum problem. Let fi be the objective function of the optimization problem, so if the minimum value problem is optimized, the fitness function is the deformation of fi, which is generally expressed by formula (2-6); If the maximum problem is optimized, the fitness function is the objective function.
fiti={1+abs(fi) fi>=01/1+fi fi>0 (2-6)
When evaluating food sources, the artificial bee colony algorithm generally makes greedy selection according to formula (2-7).
vi={xi fit(xi)<=fit(vi)vi fit(vi)>fit(xi) (2-7)
Artificial bee colony algorithm is to find the optimal food source or optimal solution through cyclic search.
Algorithm steps
Specific implementation steps of artificial bee colony algorithm:
Step 1: initialize the population: initialize various parameters, the total number of bees Sn, the number of food sources collected, i.e. the maximum number of iterations MCN and the control parameter limit, determine the problem search range, and randomly generate the initial solution xi(i=1,2,...SN) within the search range.
Step 2: calculate and evaluate the fitness of each initial solution.
Step 3: set the cycle conditions and start the cycle
Step 4: lead the bee to search the neighborhood of solution xi according to formula (2-3), generate a new solution (food source) vi, and calculate its fitness value;
Step 5: greedy selection according to equation (2-7): if the fitness value of vi is better than xi, replace xi with vi and take vi as the best solution at present, otherwise keep xi unchanged;
Step 6: calculate the probability pi of food source according to formula (2-4);
Step 7: the following bee selects the solution or food source according to the probability pi, searches and generates a new solution (food source) vi according to equation (2-3), and calculates its fitness.
Step 8: greedy selection according to formula (2-7); If the fitness of vi is better than xi, replace xi with vi and take vi as the current best solution, otherwise keep xi unchanged;
Step 9: judge whether there is a solution to give up. If so, the reconnaissance bee randomly generates a new solution according to formula (2-5) and replaces it;
Step 10: record the optimal solution so far;
Step 11: judge whether the cycle termination conditions are met. If so, the cycle ends and the optimal solution is output. Otherwise, return to step 4 to continue the search.
Partial code
global radar1
global radar2
global R
% radar1 = [350 105 305 105 175 245 415 480 40 470];
% baili = size(radar1,2);
% radar2 = [200 0 -150 110 110 110 0 110 100 -50];
% R = [140 70 150 30 25 25 25 90 40 30];
radar1 = [100 200 300 400 150 250 350 150 250 350 0 466 250 250 466 30];
baili = size(radar1,2);
radar2 = [0 0 0 0 50 50 50 -50 -50 -50 40 40 -300 300 -40 -20];
R = [40 40 40 40 40 40 40 40 40 40 20 20 260 277 20 30];
NP=40; %/* The number of colony size (employed bees+onlooker bees)*/
FoodNumber=NP/2; %/*The number of food sources equals the half of the colony size*/
maxCycle=10; %/*The number of cycles for foraging {a stopping criteria}*/
limit=0.1*maxCycle; %/*A food source which could not be improved through "limit" trials is abandoned by its employed bee*/
D= 30;
ub=ones(1,D).*50; %/*lower bounds of the parameters. */
lb=ones(1,D).*-50;%/*upper bound of the parameters.*/
runtime=1;%/*Algorithm can be run many times in order to see its robustness*/
GlobalMins=zeros(1,runtime);
Range = repmat((ub-lb),[FoodNumber 1]);
Lower = repmat(lb, [FoodNumber 1]);
Foods = rand(FoodNumber,D) .* Range + Lower;
for r=1:runtime
for i = 1:FoodNumber
ObjVal(i) = calcu(Foods(i,:));
end
Fitness = calculateFitness(ObjVal);
trial=zeros(1,FoodNumber);
BestInd=find(ObjVal==min(ObjVal));
BestInd=BestInd(end);
GlobalMin = ObjVal(BestInd);
GlobalParams=Foods(BestInd,:);
iter=1;
while ((iter <= maxCycle)),
for i=1:(FoodNumber)
Param2Change=fix(rand*D)+1;
neighbour=fix(rand*(FoodNumber))+1;
while(neighbour==i)
neighbour=fix(rand*(FoodNumber))+1;
end;
sol=Foods(i,:);
sol(Param2Change)=Foods(i,Param2Change)+(Foods(i,Param2Change)-Foods(neighbour,Param2Change))*(rand-0.5)*2;
%
ind=find(sol<lb);
libai = rand(1,D).*(ub-lb)+lb;
sol(ind)=libai(ind);
ind=find(sol>ub);
libai = rand(1,D).*(ub-lb)+lb;
sol(ind)=libai(ind);
%
ObjValSol = calcu(sol);
FitnessSol=calculateFitness(ObjValSol);
if (FitnessSol>Fitness(i))
Foods(i,:)=sol;
Fitness(i)=FitnessSol;
ObjVal(i)=ObjValSol;
trial(i)=0;
else
trial(i)=trial(i)+1;
end;
end;
prob=(0.9.*Fitness./max(Fitness))+0.1;
i=1;
t=0;
while(t<FoodNumber)
if(rand<prob(i))
t=t+1;
Param2Change=fix(rand*D)+1;
neighbour=fix(rand*(FoodNumber))+1;
while(neighbour==i)
neighbour=fix(rand*(FoodNumber))+1;
end;
sol=Foods(i,:);
sol(Param2Change)=Foods(i,Param2Change)+(Foods(i,Param2Change)-Foods(neighbour,Param2Change))*(rand-0.5)*2;
%
ind=find(sol<lb);
libai = rand(1,D).*(ub-lb)+lb;
sol(ind)=libai(ind);
ind=find(sol>ub);
libai = rand(1,D).*(ub-lb)+lb;
sol(ind)=libai(ind);
%
ObjValSol = calcu(sol);
FitnessSol=calculateFitness(ObjValSol);
if (FitnessSol>Fitness(i))
Foods(i,:)=sol;
Fitness(i)=FitnessSol;
ObjVal(i)=ObjValSol;
trial(i)=0;
else
trial(i)=trial(i)+1; %/*if the solution i can not be improved, increase its trial counter*/
end;
end;
i=i+1;
if (i==(FoodNumber)+1)
i=1;
end;
end;
ind=find(ObjVal==min(ObjVal));
ind=ind(end);
if (ObjVal(ind)<GlobalMin)
GlobalMin=ObjVal(ind);
GlobalParams=Foods(ind,:);
end;
ind=find(trial==max(trial));
ind=ind(end);
if (trial(ind)>limit)
trial(ind)=0;
sol=(ub-lb).*rand(1,D)+lb;
ObjValSol = calcu(sol);
FitnessSol=calculateFitness(ObjValSol);
Foods(ind,:)=sol;
Fitness(ind)=FitnessSol;
ObjVal(ind)=ObjValSol;
end;
fprintf('iteration = %d ObjVal=%g\n',iter,GlobalMin);
aaaaa(iter) = GlobalMin;
iter=iter+1;
end % End of ABC
storeer(r,:) = aaaaa;
end
%
% figure (1)
% a = mean(storeer);
% plot(a)
figure (2)
hold on
plot(0,0,'k*')
plot(500,0,'ks')
for i = 1:baili
hold on
plot(radar1(i),radar2(i),'ko');
cir_plot([radar1(i),radar2(i)],R(i));
end
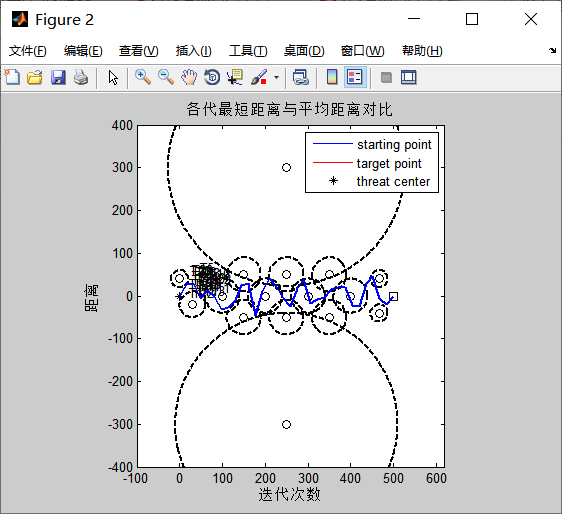
legend('starting point','target point','threat center')
axis equal
axis([-100,620,-400,400])
for i = 1:(D-1)
plot([500/(D+1)*i,500/(D+1)*(i+1)],[GlobalParams(i),GlobalParams(i+1)],'LineWidth',2);
hold on
end
plot([0,500/(D+1)*(1)],[0,GlobalParams(1)],'LineWidth',2);
plot([500/(D+1)*D,500],[GlobalParams(D),0],'LineWidth',2);
