preface

Mu Shen's code has been watched for a long time, and the video on station B has been brushed many times. He lamented that his foundation is not very solid. The bottom code of the anchor box is almost rolled over line by line. Therefore, make a summary of the whole learning part, and first put Mu Shen's station B and electronic teaching program to show his respect!
Preview of the second edition of hands-on learning in depth
Learn AI from Li Mu

The previous article mainly summarized the anchor box and how to generate the anchor box centered on each pixel of an image. The specific steps can be:
Personal summary of SSD target detection (1) -- generation of anchor box

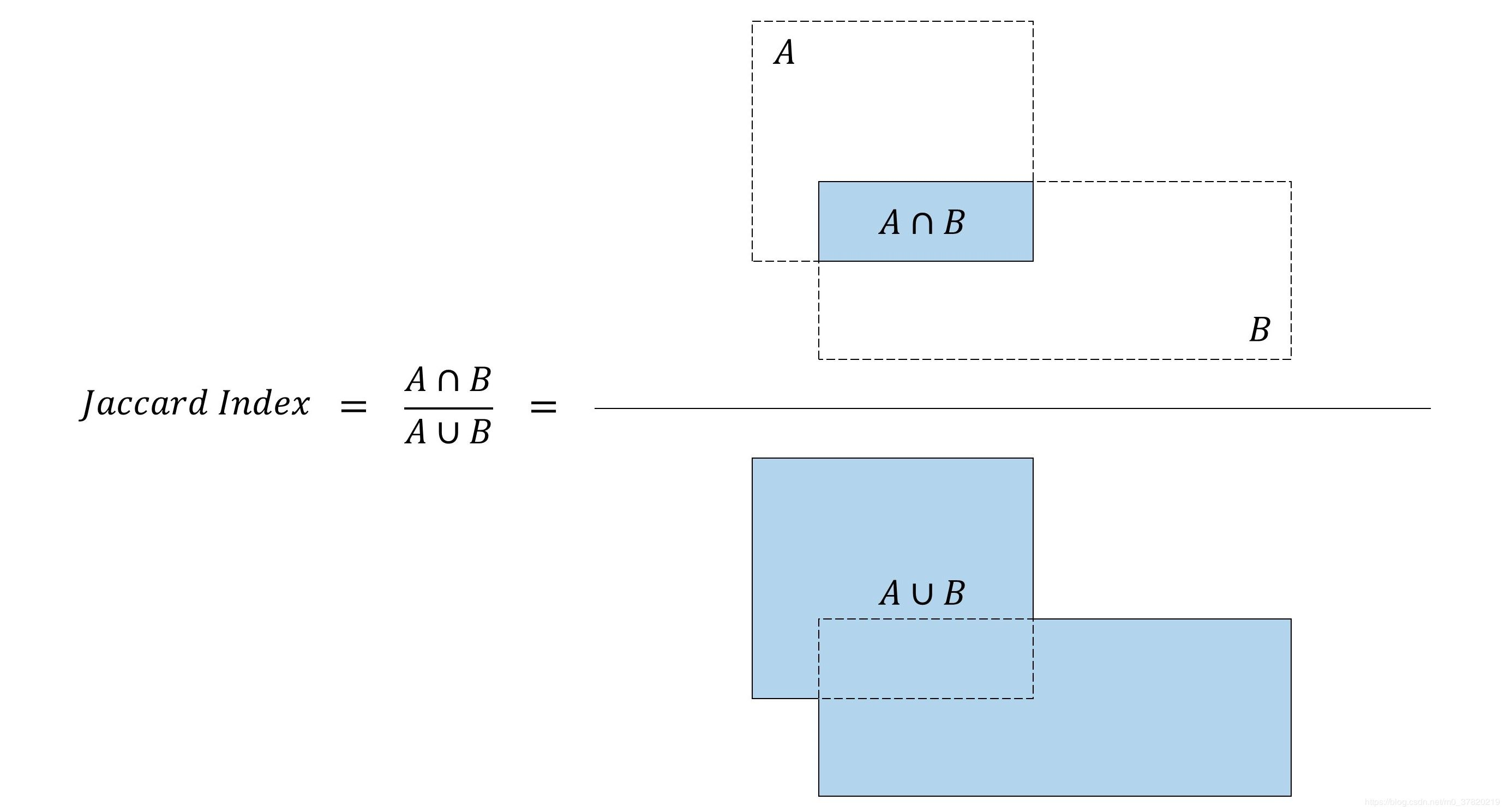
Cross merge ratio

In the target detection task, if the real frame is known, how to judge the quality of the generated anchor frame and how to select the optimal anchor frame?
Generally, we will measure it by intersection and union ratio, i.e. Jaccard coefficient. It should be noted that the calculation result of Jaccard coefficient is between 0-1. The closer it is to 0, the less the overlap between anchor frame and real frame, and the closer it is to 1, the higher the overlap between anchor frame and real frame; Equal to 0 is completely non coincident, equal to 1 is completely coincident

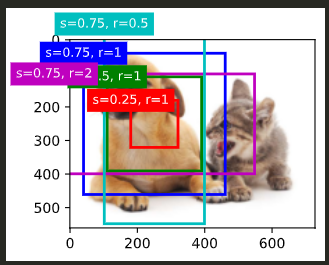
Taking the cat and dog pictures used in the previous chapter as an example, suppose that we have defined the real frames of cat and dog in advance, and assume that we have the coordinate relative values of five anchors and the label data of two real frames (ground_truth). The first element of the label data of each real frame is the category. In this example, 0 represents dog and 1 represents cat;

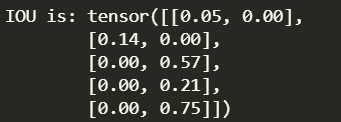
We can calculate the IOU of each anchor frame and ground_truth one by one. The specific calculation is as follows:

# Built anchors and real boxes
# Subtract the x coordinate of anchor frame and real frame
# The y coordinates of anchor frame and real frame are subtracted
ground_truth = torch.tensor([[0, 0.1, 0.08, 0.52, 0.92],
                         [1, 0.55, 0.2, 0.9, 0.88]])
anchors = torch.tensor([[0, 0.1, 0.2, 0.3], [0.15, 0.2, 0.4, 0.4],
                    [0.63, 0.05, 0.88, 0.98], [0.66, 0.45, 0.8, 0.8],
                    [0.57, 0.3, 0.92, 0.9]])
# Part of calculating intersection and union ratio
box_area = lambda boxes: ((boxes[:, 2] - boxes[:, 0]) *(boxes[:, 3] - boxes[:, 1]))
areas1 = box_area(anchors.unsqueeze(dim=0)[0,:,:])
areas2 = box_area(ground_truth.unsqueeze(dim=0)[0,:,:][:,1:])
# Take out the larger value of the intersection of the anchor box and the real box in the upper left corner, and take the first two coordinates of anchors while maintaining the current dimension
inter_upperlefts = torch.max(anchors.unsqueeze(dim=0)[0,:,:][:, None, :2], ground_truth.unsqueeze(dim=0)[0,:,:][:,1:][:, :2])
# Take out the smaller value of the intersection of the anchor box and the real box in the lower right corner, and take the last two coordinates of anchors while maintaining the current dimension
inter_lowerrights = torch.min(anchors.unsqueeze(dim=0)[0,:,:][:, None, 2:], ground_truth.unsqueeze(dim=0)[0,:,:][:,1:][:, 2:])
inters = (inter_lowerrights - inter_upperlefts).clamp(min=0)
# Calculate intersection area____ Rectangle____ Length * width
inter_areas = inters[:, :, 0] * inters[:, :, 1]
# Anchor frame area + real frame area - intersection area
union_areas = areas1[:, None] + areas2 - inter_areas
# Intersection and union ratio = proportion of intersection area to Union area
# The data format is the scaling of IOU values of M anchor boxes and N categories of real boxes
IOUS = inter_areas/union_areas

After calculation, return the value of IOU. After further encapsulation, you can get the function of calculating intersection and union ratio, and provide the specific coordinate information of anchor frame and real frame as parameters

def box_iou(boxes1, boxes2):
    """Calculate the intersection and union ratio of pairs in the list of two anchor boxes or bounding boxes"""
    box_area = lambda boxes: ((boxes[:, 2] - boxes[:, 0]) *
                              (boxes[:, 3] - boxes[:, 1]))
    areas1 = box_area(boxes1)
    areas2 = box_area(boxes2)

    inter_upperlefts = torch.max(boxes1[:, None, :2], boxes2[:, :2])
    inter_lowerrights = torch.min(boxes1[:, None, 2:], boxes2[:, 2:])
    inters = (inter_lowerrights - inter_upperlefts).clamp(min=0)

    inter_areas = inters[:, :, 0] * inters[:, :, 1]
    union_areas = areas1[:, None] + areas2 - inter_areas
    return inter_areas / union_areas

The result of calculating the intersection and union ratio of the real frame and the anchor frame is shown in the figure below. The shape is (5,2), and each element corresponds to two categories respectively. For example, [0.00,0.75] indicates that the intersection and union ratio of the current anchor frame and category 2 is 0.75

Assign anchor boxes to real boxes

After calculating the intersection and union ratio IOU, we can get that different anchor frame anchors correspond to the same real frame ground_ For the intersection and union ratio of truth, the label data of the real box is composed of category + offset. For the anchor box with the largest IOU value, we can think that the anchor box is closest to the real box, so we can assign the category and offset of a real box to the anchor box The specific implementation code is as follows

1. Obtain the relevant information of intersection and merger ratio, mainly obtain the size of intersection and merger ratio and what is the classification of the size
2. Build the index matrix of real box and anchor box
3. Create row and column mask, full fill - 1
4. Create a cycle according to the number of real boxes. If the index is found under the category with the largest IOU value, fill the row \ column where the value is located with - 1 until all real boxes are assigned to the anchor box

# Assign part of the real box
num_anchors, num_gt_boxes = anchors.shape[0], ground_truth.shape[0]
anchors_bbox_map = torch.full((num_anchors,), -1, dtype=torch.long)
# Returns the maximum intersection union ratio and its subscript. The format of IOUS is, M anchor boxes and N category real boxes; Obtain the value of the maximum IOU on N categories; Get the subscript of the maximum IOU value on N categories
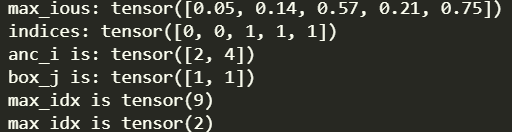
max_ious, indices = torch.max(IOUS, dim=1)
print('max_ious:',max_ious)
print('indices:',indices)
# Get the array subscript that exceeds the threshold on maxiou
anc_i = torch.nonzero(max_ious >= 0.5).reshape(-1)
# Get the value exceeding the threshold on indices
box_j = indices[max_ious >= 0.5]
# # Establish corresponding coordinates
# anc_i corresponds to array subscript, box_j value corresponding to subscript index
anchors_bbox_map[anc_i] = box_j
# There are five columns - corresponding to five anchor boxes, two rows, corresponding to two real boxes, create a blank shape, and fill all with - 1
col_discard = torch.full((num_anchors,), -1)
row_discard = torch.full((num_gt_boxes,), -1)
# Assign real borders to anchor boxes based on the number of real borders
for _ in range(num_gt_boxes):
    # Get the index of the largest IOU. When argmax is used, the index is returned in sequence, similar to returning the index after flattening into one dimension. For example, for a tensor with shape (5,2), if the maximum value is in the position of tensor[4][1], it will directly return 9
    max_idx = torch.argmax(IOUS)
    print('max_idx is',max_idx)
    # The remainder with the real border is used as the column index
    box_idx = (max_idx % num_gt_boxes).long()
    # Quotient line and frame as real
    anc_idx = (max_idx / num_gt_boxes).long()
    # Decide which anchor box is assigned to the real box, that is, the category is assigned to the corresponding index
    anchors_bbox_map[anc_idx] = box_idx
    # Assign - 1 to the row and column where the largest IOU is located, because the real box of a category only assigns the anchor box with the largest IOU, so the category of the column can be deleted
    IOUS[:, box_idx] = col_discard
    IOUS[anc_idx, :] = row_discard

After running the code, we can get several key variables:

1. max_ious: after the calculation of intersection and union ratio, the maximum value of intersection and union ratio is taken under different classifications;
2. indices: the category to which different combinations belong after taking the maximum;
3. anc_i: The value of intersection and union ratio greater than the threshold of thresholds;
4. box_j: anc_i) corresponding category;
5. max_idx: the index of the maximum iou value in the loop built according to the real box

Through the operation of the above code, we can assign two real boxes to the anchor box with the largest iou value under the current category. We further encapsulate and provide real box information, anchor box information, iou threshold, etc. for subsequent code calls,

def assign_anchor_to_bbox(ground_truth, anchors, device, iou_threshold=0.5):
    """Assign the closest real bounding box to the anchor box"""
    num_anchors, num_gt_boxes = anchors.shape[0], ground_truth.shape[0]
    jaccard = box_iou(anchors, ground_truth)
    # Through full, use num_anchors construction coordinates, there are as many lines as there are anchor boxes
    anchors_bbox_map = torch.full((num_anchors,), -1, dtype=torch.long,
                                  device=device)
    max_ious, indices = torch.max(jaccard, dim=1)
    anc_i = torch.nonzero(max_ious >= iou_threshold).reshape(-1)
    box_j = indices[max_ious >= iou_threshold]
    # Establish corresponding coordinates
    anchors_bbox_map[anc_i] = box_j
    col_discard = torch.full((num_anchors,), -1)
    row_discard = torch.full((num_gt_boxes,), -1)
    for _ in range(num_gt_boxes):
        # Gets the index of the largest IOU
        max_idx = torch.argmax(jaccard)
        box_idx = (max_idx % num_gt_boxes).long()
        anc_idx = (max_idx / num_gt_boxes).long()
        anchors_bbox_map[anc_idx] = box_idx
        jaccard[:, box_idx] = col_discard
        jaccard[anc_idx, :] = row_discard
    return anchors_bbox_map

Take the information of the real box and anchor box provided by us as the input, and finally return to anchors_bbox_map, which stores the category corresponding to the iou value of the current anchor box and the real box, - 1 is the category not less than the iou threshold, and is uniformly marked as - 1

anchors_bbox_map is : tensor([-1, 0, 1, -1, 1])