Original address: https://sean.cm/a/polygon-clipping-pt1

Greiner Hormann clipping algorithm cannot handle coincident lines. So I studied and wrote another article that applies to all polygons.

Read on here: Polygon clipping (Part 2)

problem

First, let's define the problem,

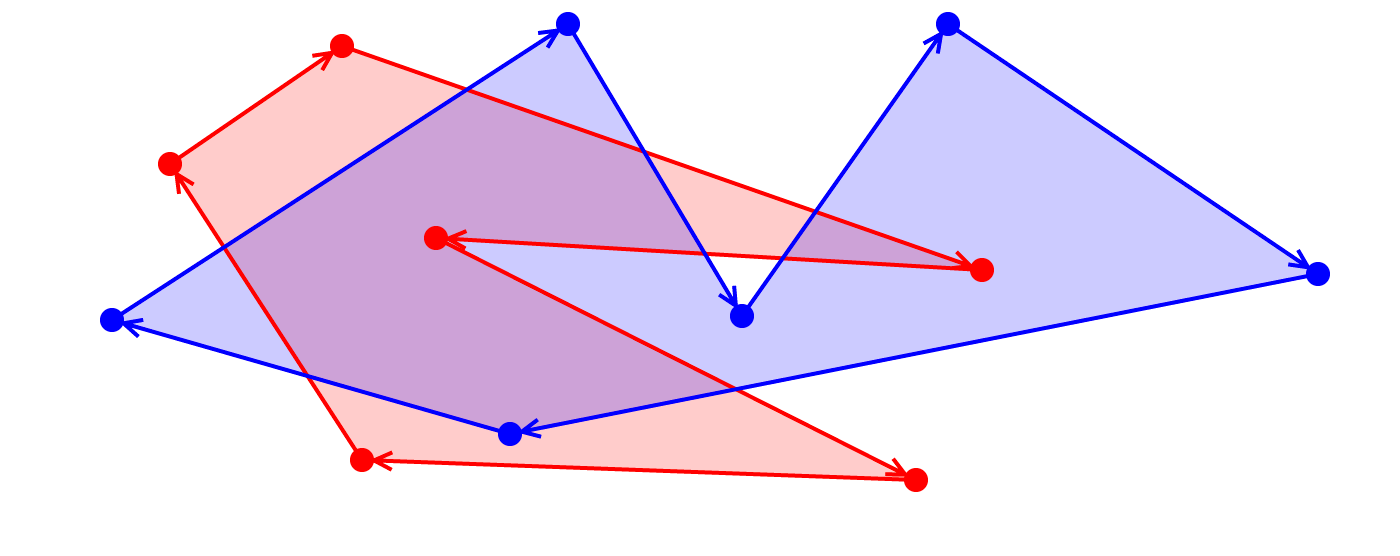
Suppose you have two polygons, each in 2D

var poly1 = [ // red
  [ 181, 270 ],
  [  85, 418 ],
  [ 171, 477 ],
  [ 491, 365 ],
  [ 218, 381 ],
  [ 458, 260 ]
];
var poly2 = [ // blue
  [ 474, 488 ],
  [ 659, 363 ],
  [ 255, 283 ],
  [  56, 340 ],
  [ 284, 488 ],
  [ 371, 342 ]
];

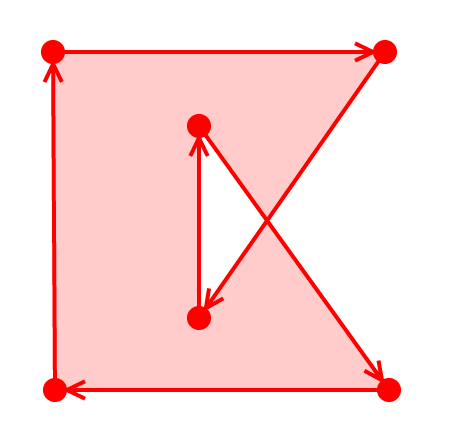
Parity rule

Polygon following Parity rule To determine whether a point is considered "inside" of the area.

The basic rule is to imagine that you are scanning from left to right with a horizontal line. Each time you cross the edge, you switch between the outside and the inside.

So: Given these two polygons, how do we calculate different Boolean operations?

Basic concept

First, let's define some basic rules

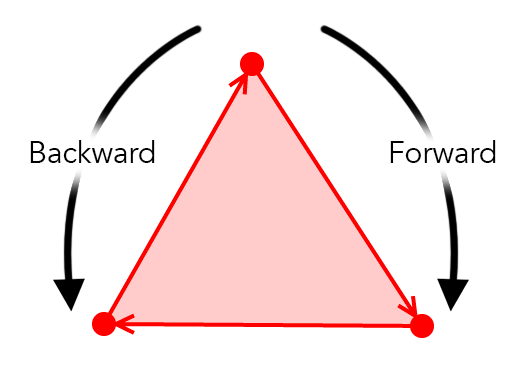
Clockwise vs. counterclockwise movement

If we sit on any point of the polygon, we can always move forward or backward

Clockwise only means moving in the direction of the arrow, counterclockwise is the opposite

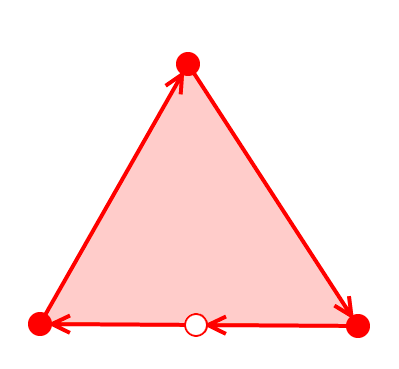
Insertion point

During processing, we need to insert points into the polygon. As long as we are smart about how to insert them, it will not change the shape of the polygon:

intersection

Identifying and classifying intersections is the magic of the algorithm

If you think about it, every operation we will perform (intersection, union, difference) will produce a polygon containing all intersections between polygons

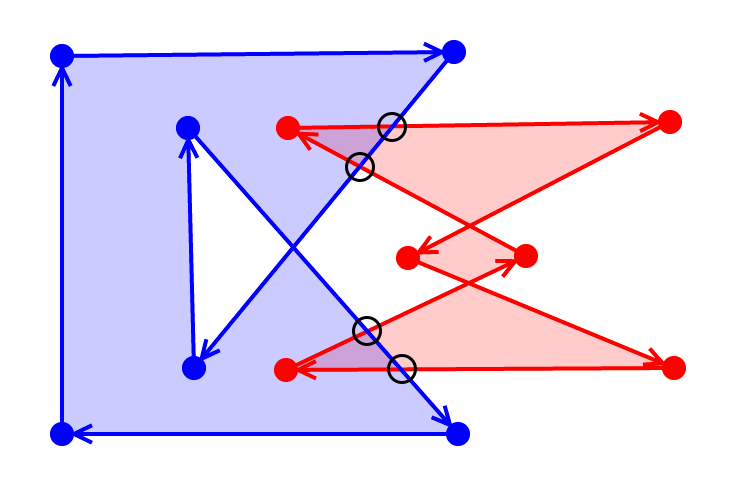
We don't care about intersections in the same polygon

Also: if you imagine that we are walking along a polygon and meet an intersection, we have three choices

1. Keep on the same polygon (this is meaningless)

2. Switch polygons and start moving clockwise

3. Switch polygons and start moving counterclockwise

 

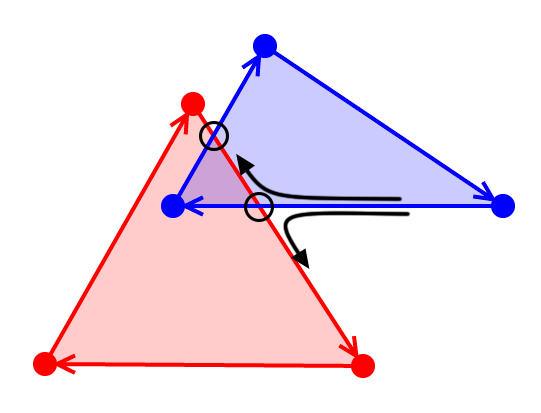
Therefore, if we can intelligently choose the direction at each intersection, we can track the correct result shape

Intersection example

Imagine, let's imagine, we're tracking the result of the union of two polygons

At each intersection, we want to move in the direction of continued growth in the final shape

We can do this:

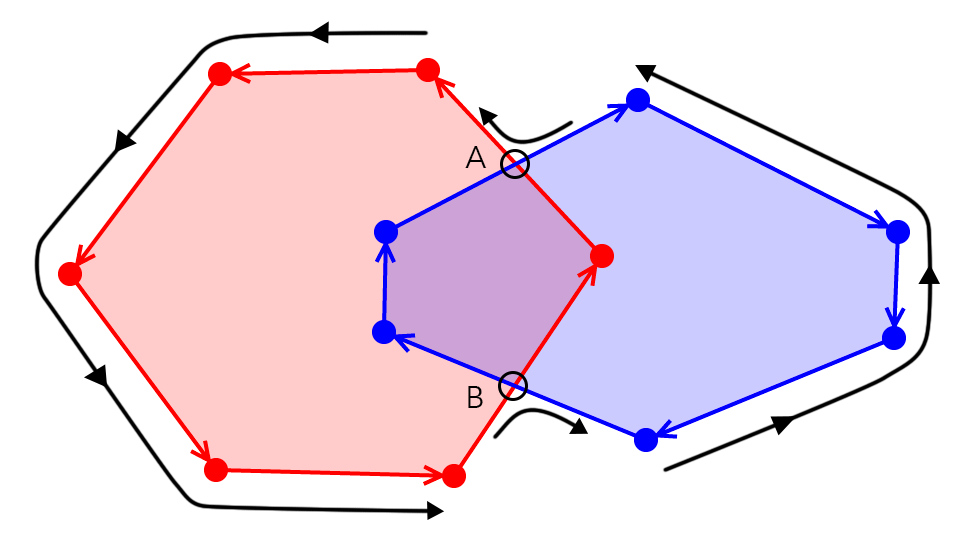
We can also get the same result in the opposite direction:

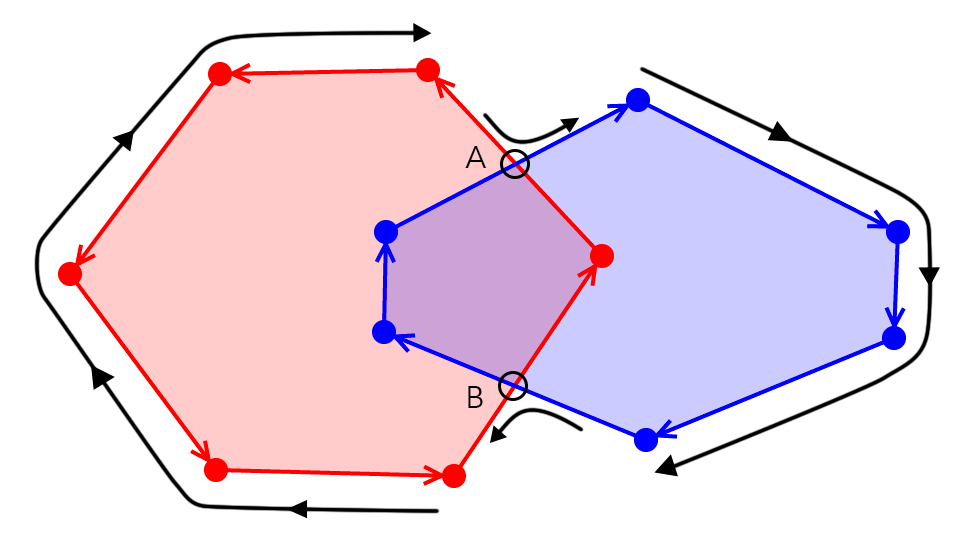
What can we say is right about all four decisions?

At each intersection, we always move away from the polygon we leave

So, for example, if we drive along Blue and then encounter an intersection, we should continue to drive away from Blue along Red

What's the difference? This is Red Blue (subtract the Blue area from Red):

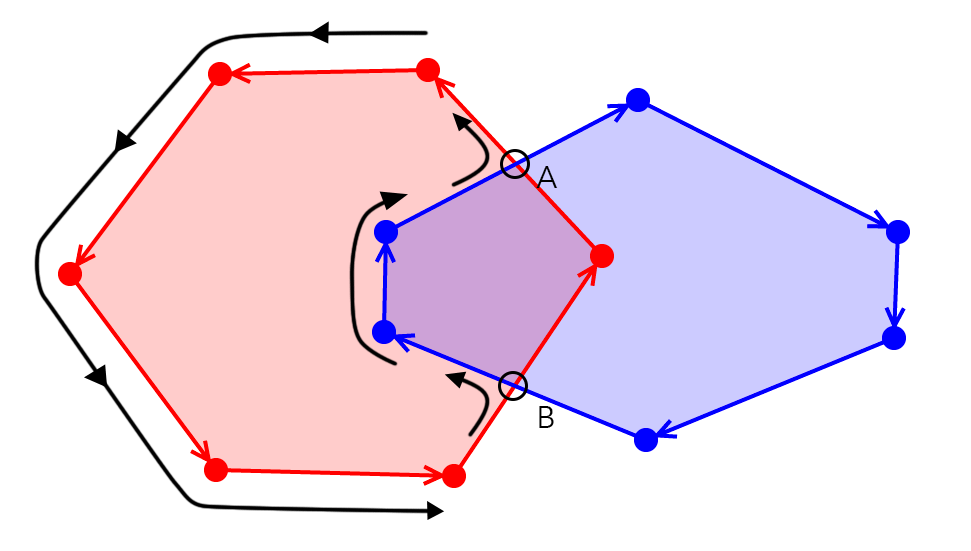
In the other direction:

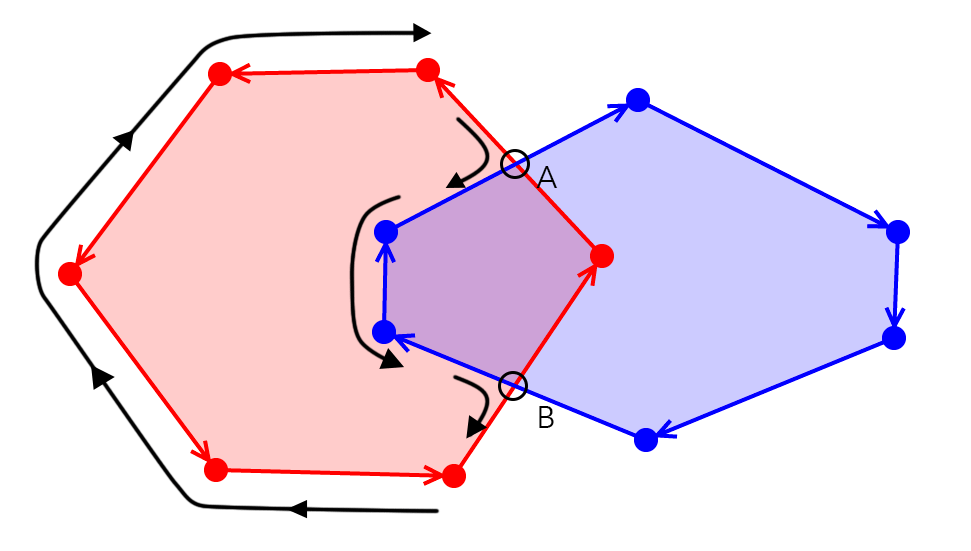
What can we say about this?

When we switch from red to blue, we enter red. When we switch from blue to red, we stay away from red

So we have two basic decisions:

1. When switching from red to blue, do we enter or stay away from red?

2. When switching from blue to red, do we enter or stay away from blue?

For a union, the answer always leaves But for red blue (red minus Blue), we want to go into red and stay away from blue. If you play, you will notice that intersection means always entering where you want to leave

This gives us the watch below

Operator	Into Red?	Into Blue?
Union	False	False
Red minus Blue(Red - Blue)	True	False
Blue minus Red(Blue - Red)	False	True
Intersection	True	True

Cross entrance / cross exit

We don't know how to get in or out - we only know to move clockwise and counterclockwise along the polygon. How can we agree the two

If we take two points on both sides of an intersection and test whether they are in another polygon, we can ensure that one point is outside and one point is inside:

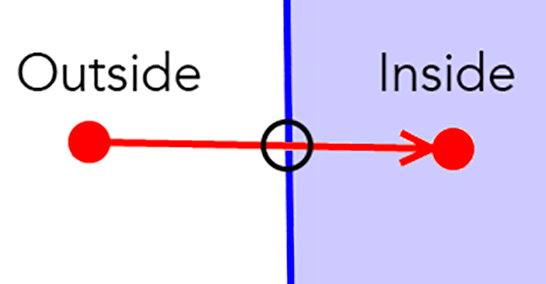
If the first point is outside, we can think that the line enters the polygon through the intersection. If the first point is included, the line leaves the polygon through the intersection

So we really just need to mark each intersection as a cross entrance / cross exit

When we drive along a path, each intersection will switch whether we are inside or outside. It must

Therefore, we only need to calculate whether the first point is inside another polygon. If so, then the first intersection is a crossing exit - otherwise, the first intersection is a crossing entrance

And since each intersection on the path switches between entry and exit, we don't have to continue to test whether the point is internal or external (which is expensive)

performance

Finally, it is important to recognize that the intersection is the intersection entrance or exit relative to the polygon

This means that there are four possibilities at each intersection

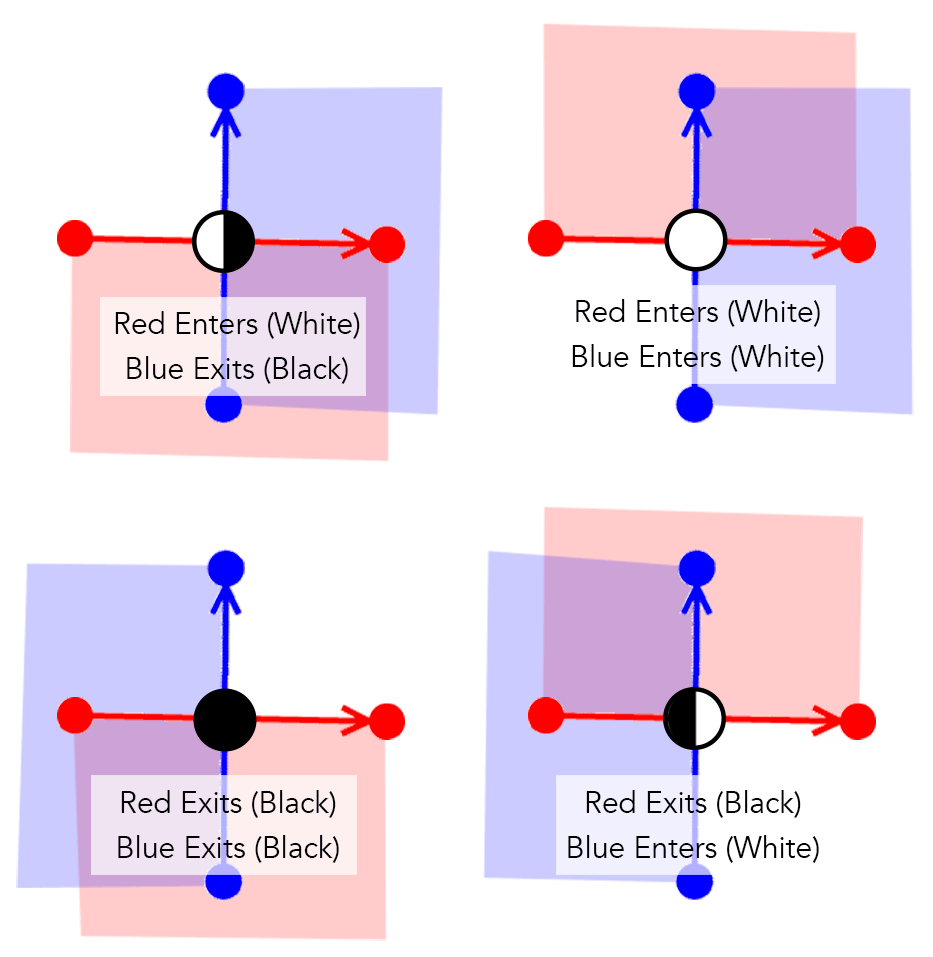
White represents entry and black represents exit. The left hemisphere is red and the right hemisphere is blue

In fact, for each intersection, we will insert a point in each polygon. So there are two points in each polygon. Each point tracks whether it enters or exits

Now we have the code ready

Step 1 Convert polygons to linked lists

Double linked list is a useful polygon representation for this algorithm, because we will insert points and traverse at the same time. By using a double linked list, we don't have to worry that insertion will destroy traversal

We also need to track whether a point is an intersection, so we can initialize it from false:

function UpgradePolygon(p){
  // converts a list of points into a double linked list
  var root = null;
  for (var i = 0; i < p.length; i++){
    var node = {
      point: p[i],
      intersection: false,
      next: null,
      prev: null
    };
    if (root === null){
      // root just points to itself:
      //    +-> (root) <-+
      //    |            |
      //    +------------+
      node.next = node;
      node.prev = node;
      root = node;
    }
    else{
      // change this:
      //    ...-- (prev) <--------------> (root) --...
      // to this:
      //    ...-- (prev) <--> (node) <--> (root) --...
      var prev = root.prev;
      prev.next = node;
      node.prev = prev;
      node.next = root;
      root.prev = node;
    }
  }
  return root;
}

Step 2 Calculate and insert intersections

Next, we need to traverse each edge combination to see if they intersect. If they do intersect each other, we need to insert intersections in the polygon

Line intersection

First, we need an auxiliary function to calculate the intersection of two lines:

function LinesIntersect(a0, a1, b0, b1){
  var adx = a1[0] - a0[0];
  var ady = a1[1] - a0[1];
  var bdx = b1[0] - b0[0];
  var bdy = b1[1] - b0[1];

  var axb = adx * bdy - ady * bdx;
  var ret = {
    cross: axb,
    alongA: Infinity,
    alongB: Infinity,
    point: [Infinity, Infinity]
  };
  if (axb === 0)
    return ret;

  var dx = a0[0] - b0[0];
  var dy = a0[1] - b0[1];

  ret.alongA = (bdx * dy - bdy * dx) / axb;
  ret.alongB = (adx * dy - ady * dx) / axb;

  ret.point = [
    a0[0] + ret.alongA * adx,
    a0[1] + ret.alongA * ady
  ];

  return ret;
}

It calculates the intersection of two lines and returns how far along the intersection of each line. Therefore, for example, if alongA is 0.75, the intersection occurs at 75% from a0 to a1  

These values are important because they may be negative or greater than 1. Therefore, if the two lines actually intersect, we need to test between alongA and alongB0 and 1 (excluding)

Next non intersection

Because we will insert the intersection in our linked list, there is a help function to find the next non intersection

function NextNonIntersection(node){
  do{
    node = node.next;
  } while (node.intersection);
  return node;
}

Each edge pair

Now we can write code that iterates over each edge combination:

var root1 = UpgradePolygon(poly1);
var root2 = UpgradePolygon(poly2);

var here1 = root1;
var here2 = root2;
do{
  do{
    //
    // TODO: test intersection between:
    //    here1 -> NextNonIntersection(here1)  and
    //    here2 -> NextNonIntersection(here2)
    //
    here2 = NextNonIntersection(here2);
  } while (here2 !== root2);
  here1 = NextNonIntersection(here1);
} while (here1 !== root1);

Intersection test

Given two nodes, we can test the intersection:

var next1 = NextNonIntersection(here1);
var next2 = NextNonIntersection(here2);

var i = LinesIntersect(
  here1.point, next1.point,
  here2.point, next2.point
);

if (i.alongA > 0 && i.alongA < 1 &&
  i.alongB > 0 && i.alongB < 1){
  //
  // TODO: insert intersection points in both polygons at
  //       the correct location, referencing each other
  //
}

Insert intersection

Finally, if two edges intersect, we insert our intersection between two non intersections

In order to insert it in the correct position, we must track the alongA and alongB values to ensure that if the two intersections are on the same edge, they are inserted in the correct order

We're going to create two nodes, one for each polygon -- but these nodes should point to each other so that we can "jump" between polygons later when we encounter an intersection

var node1 = {
  point: i.point,
  intersection: true,
  next: null,
  prev: null,
  dist: i.alongA,
  friend: null
};
var node2 = {
  point: i.point,
  intersection: true,
  next: null,
  prev: null,
  dist: i.alongB,
  friend: null
};

// point the nodes at each other
node1.friend = node2;
node2.friend = node1;

var inext, iprev;

// find insertion between here1 and next1, based on dist
inext = here1.next;
while (inext !== next1 && inext.dist < node1.dist)
  inext = inext.next;
iprev = inext.prev;

// insert node1 between iprev and inext
inext.prev = node1;
node1.next = inext;
node1.prev = iprev;
iprev.next = node1;

// find insertion between here2 and next2, based on dist
inext = here2.next;
while (inext !== next2 && inext.dist < node2.dist)
  inext = inext.next;
iprev = inext.prev;

// insert node2 between iprev and inext
inext.prev = node2;
node2.next = inext;
node2.prev = iprev;
iprev.next = node2;

Step 3 Calculate cross entry / exit

We know that intersections alternate between entry and exit. But what is the first intersection? Is it an entrance or an exit

Simple: if the first point of a polygon is within another polygon, the first intersection must be an exit

However, calculating whether a point is inside a polygon is actually a little complicated

Point in polygon

function PointInPolygon(point, root){
  var odd = false;
  var x = point[0];
  var y = point[1];
  var here = root;
  do {
    var next = here.next;
    var hx = here.point[0];
    var hy = here.point[1];
    var nx = next.point[0];
    var ny = next.point[1];
    if (((hy < y && ny >= y) || (hy >= y && ny < y)) &&
      (hx <= x || nx <= x) &&
      (hx + (y - hy) / (ny - hy) * (nx - hx) < x)){
      odd = !odd;
    }
    here = next;
  } while (here !== root);
  return odd;
}

PointInPolygon works by counting the number of edges where horizontal lines intersect. The horizontal line is from (- Infinity, y) to (x, y). It only cares whether the number of intersections is odd or even. It is based on Ray casting.

Alternate entry / exit

Now we can easily calculate whether an intersection is an entrance or an exit:

function CalculateEntryExit(root, isEntry){
  var here = root;
  do{
    if (here.intersection){
      here.isEntry = isEntry;
      isEntry = !isEntry;
    }
    here = here.next;
  } while (here !== root);
}

var is1in2 = PointInPolygon(root1.point, root2);
var is2in1 = PointInPolygon(root2.point, root1);

CalculateEntryExit(root1, !is1in2);
CalculateEntryExit(root2, !is2in1);

Step 4 Generate results

We've come a long way! This is what we have so far

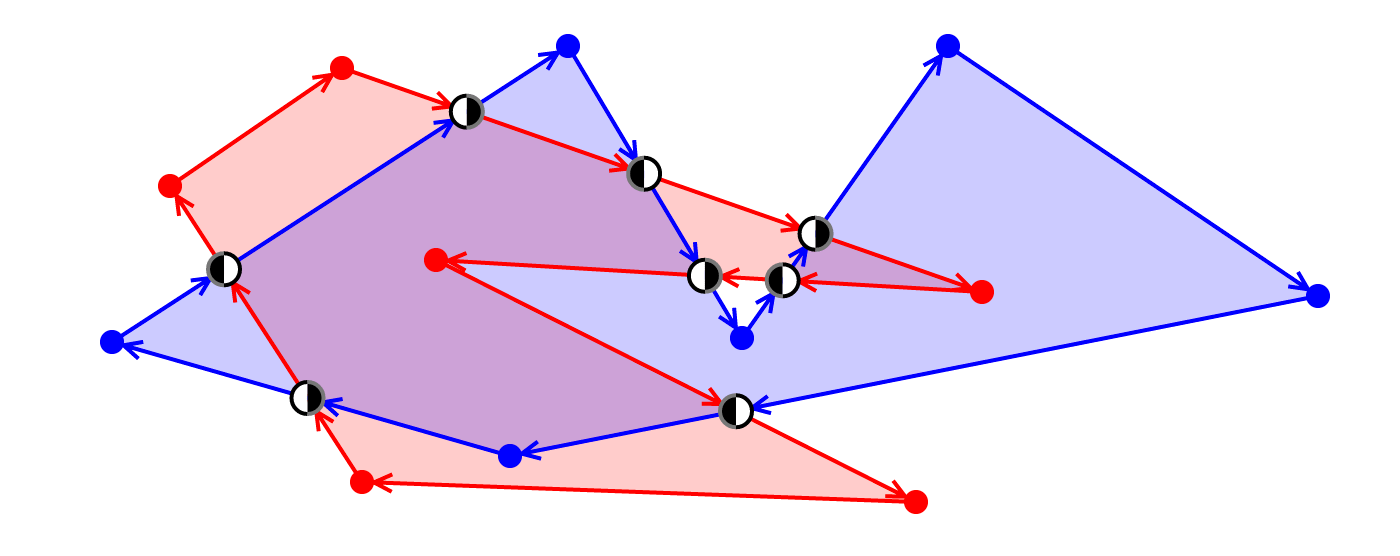
We have calculated and inserted intersections and marked them as the entry or exit of each polygon

Now is the interesting part!

Where to start

Where do we start tracking results? We can't just select one random point, because some points can actually be completely deleted from the result

Since all operations include each intersection, we should start by looking for unprocessed intersections

We mark each intersection we add to the final result as processed

Then we just keep tracking until we no longer have any intersection to deal with

var result = [];
var isect = root1;
var into = [intoBlue, intoRed]; // explained below
while (true){
  do{
    if (isect.intersection && !isect.processed)
      break;
    isect = isect.next;
  } while (isect !== root1);
  if (isect === root1)
    break;

  //
  // TODO: process isect
  //
}

In which direction

Finally, we come to the Crux:

When we meet an intersection, how do we know which direction to turn?

Let's reason:

Is Entry?	Move Into?	Move Forward?
True	True	True
True	False	False
False	True	False
False	False	True

Therefore, if, we should move forward isEntry === intoPoly

Since the polygon we are in switches back and forth, we only need to store intoBlue and intoRed in the into list to make our decision dynamic, and use their curpoly as an index

var curpoly = 0;
var clipped = [];

var here = isect;
do{
  // mark intersection as processed
  here.processed = true;
  here.friend.processed = true;

  var moveForward = here.isEntry === into[curpoly];
  do{
    clipped.push(here.point);
    if (moveForward)
      here = here.next;
    else
      here = here.prev;
  } while (!here.intersection);

  // we've hit the next intersection so switch polygons
  here = here.friend;
  curpoly = 1 - curpoly;
} while (!here.processed);

result.push(clipped);

No intersection

If there is no intersection?

Our result set will be empty... This may be true or false - depending on the operation

A simple check is enough to fix it:

if (result.length <= 0){
  if (is1in2 === intoBlue)
    result.push(poly1);
  if (is2in1 === intoRed)
    result.push(poly2);
}

demonstration

Click here to start the demo!

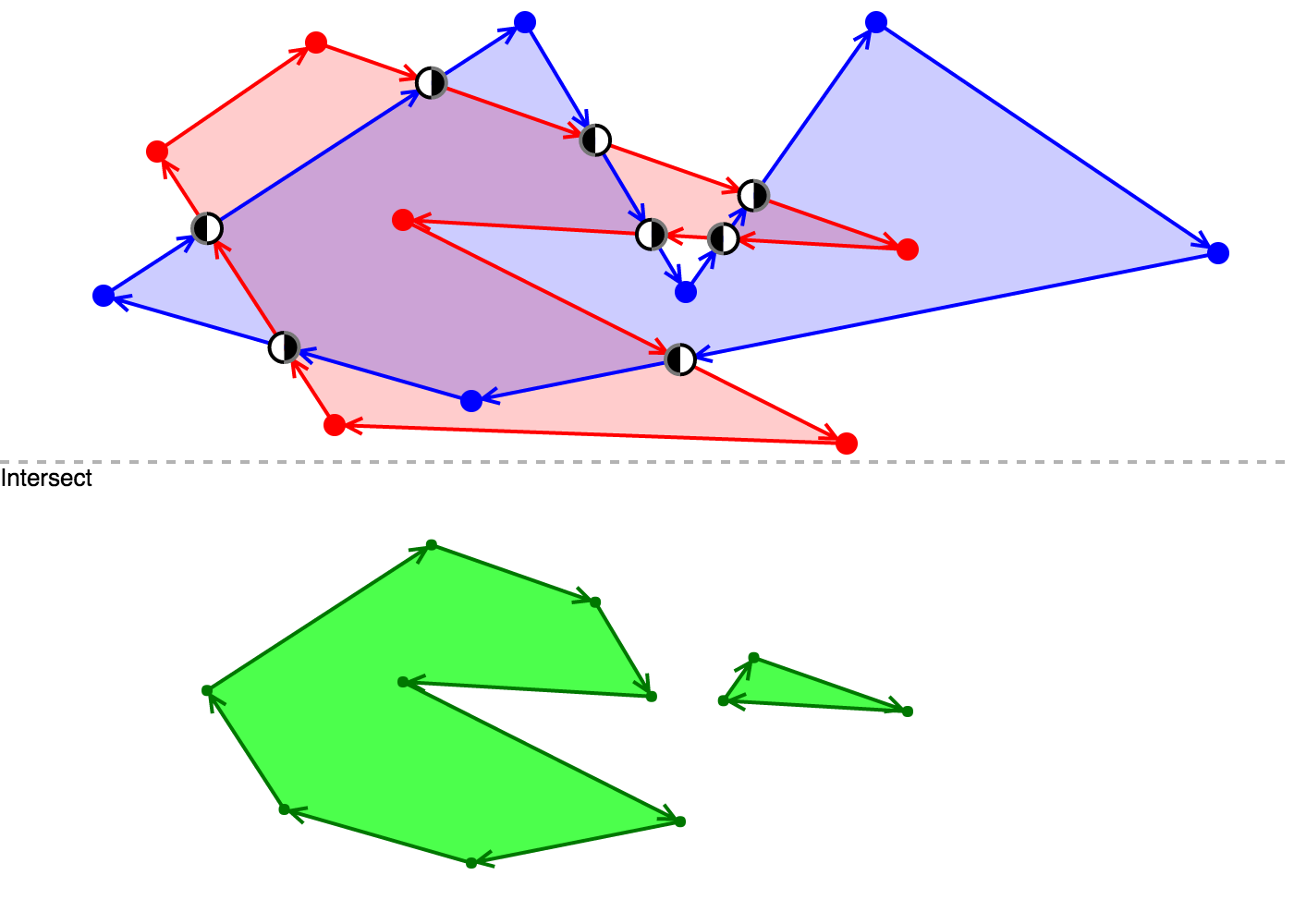
You can drag the points of each polygon and toggle the operation by clicking the button.

Appendix: restrictions

Sorry, this algorithm has a serious limitation:

You cannot have perfectly overlapping points or edges

If you think about it, it makes sense: the whole algorithm is based on the idea of intersection

If points or edges overlap directly, you won't get that good jump effect

The original paper suggested a little "scrambling" so that the lines would not overlap completely. At first I thought it was a small adjustment and there would be no problem

But I was wrong

Disturbing points can destroy the data - so potentially important attributes of the source data (for example, smooth edges) become invalid

Fortunately, I studied another algorithm to deal with everything and wrote a follow-up article

Read on here: Polygon clipping (Part 2)