The original paper is: "Pattern Classification with Corrupted Labeling via Robust Broad Learning System"
The idea of GRBLS:
The aforementioned BLS models are based on the mean square error (MSE) criterion to fit the approximation errors [23]. In fact, MSE aims to measure the sum of quadratic loss of data, and the approximation results would skew to the data with large errors. ... The purpose of the current paper is to alleviate the negative impact of data with corrupted labels on BLS.By rewriting the objective function of BLS from the matrix form to a error vector form, we conduct a maximum likelihood estimation (MLE) on the approximation errors. Then a MLE-like estimator can be gotten tomodel the residuals in BLS. An interesting point is that if the probability density function of errors is predefined as the Gaussian distribution, the MLE-like estimator can degenerate to the MSE criterion. Obviously, the presence of label outliers in the data causes the error distribution to depart from Gaussianity, which is the probabilistic interpretation of lack of robustness in standard BLS. ...
This article is to solve the problem of negative impact of data with corrupted labels on BLS. The basic assumption of BLS for residuals can be regarded as satisfying Gaussian distribution, but it is obvious that Gaussian distribution can not meet all data sets. In the paper "regulated robust broad learning system for uncertain data modeling", a hypothesis has been made that it satisfies the Laplace distribution and has achieved good results under some experimental conditions, but like the basic BLS, the "audience" is relatively small, and ENRBLS also makes me feel very strange. MLE is introduced in this paper. The BLS with this operator can degenerate into a BLS obeying Gaussian distribution, so I think GRBLS is better in theory. Part G of GRBLS is useful to the basic knowledge of manual learning. The optimization based on manifold is used in the paper "discriminative graph regulated broad learning system for image recognition", and the relevant knowledge is more complete. The article also shows the effectiveness of manifold learning.
BLS:
slightly
Manifold learning:
manifold learning is to maintain the internal structure of data when performing a series of operations such as dimensionality reduction. The important part of the operator related to manifold is the Adjacency graph, which reflects the adjacent relationship between data(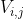
Yes
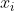And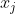
Relationship).
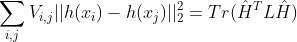
H is mapping result. Tr(.) Is the trace of the matrix,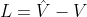
L is graph Laplacian,
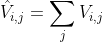This part is called diagonal entries. Of course, normalized graph Laplacian is used in the article discriminatory graph regulated broad learning system for image recognition.
The Proposed Method:
error vector e is defined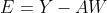
. The probability density function is defined
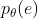. The equivalent likelihood function is
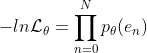, where 
,
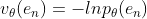The goal has changed from the original problem to:
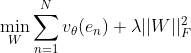
There are several basic assumptions for solving the problem:
①Symmetry: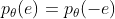 
② Monotonicity: For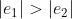 
, 
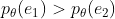
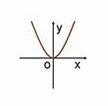
Solution to the problem:
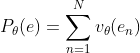
Expand the above formula to the first order (the remainder is directly estimated by the last part), there are
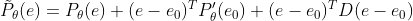
D stands for Hessian matrix, which says in the original text:
As the error residuals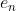 
are i.i.d., the mixed derivatives must be 0 for 
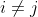, matrix D should be diagonal.
Combined with the previous assumptions, we can get:
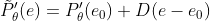
By assuming
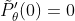
Hessian Matrix :
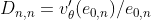
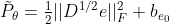
The original question becomes:
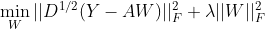
Add the previous part G:
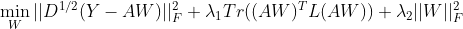
The solutions are:
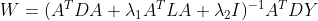
Recurrence:
All the files have been uploaded to github, GRBLS
Width learning BLS section:
I usually use the format of the code saved on the official website before. How can I write such a good format, Gucci. A random piece is pasted below
main function:
clear;
warning off all;
format compact;
if ~exist('num.mat','file')
experiment_num=0;
else
load('num.mat'); %Record the number of experiments so that the previous data will not be overwritten when generating data
end
prop = 0.4 ;
train_num = 430;
test_num = 253;
load('E:\image-about\dataBase\breast_cancer\breast_cancer.mat')
[train_x,train_y,test_x,test_y,NN] = shuffle_index(x,y,train_num,test_num);
[contaminated_train_y, C_id, contamination_num] = contaminate_label(train_y,prop,NN.train);
save('C_id.mat','C_id','contamination_num');
clear x y C_id
lambda1 = 2^(0); %------manifold learning criterion
lambda2 = 2^(-5); %------the regularization parameter
best_test = 0 ;
result = [];
k = 10; %-------k-NN
options = [];
options.NeighborMode = 'KNN';
options.k = k;
options.WeightMode = 'Binary';
options.t = 1;
file_name_1 = ['test_result/test_result ',num2str(experiment_num),'/contamination_proportion ', num2str(prop)];
for NumFea= 1:7 %searching range for feature nodes per window in feature layer
for NumWin=1:8 %searching range for number of windows in feature layer
file_name = [file_name_1 ,'/NumFea ',num2str(NumFea),'/NumWin ', num2str(NumWin)];
if ~isfolder(file_name)
mkdir(file_name);
end
for NumEnhan=2:50 %searching range for enhancement nodes
clc;
rng('shuffle');
for i=1:NumWin
WeightFea=2*rand(size(train_x,2)+1,NumFea)-1;
% b1=rand(size(train_x,2)+1,N1); % sometimes use this may lead to better results, but not for sure!
WF{i}=WeightFea;
end %generating weight and bias matrix for each window in feature layer
WeightEnhan=2*rand(NumWin*NumFea+1,NumEnhan)-1;
fprintf(1, 'Fea. No.= %d, Win. No. =%d, Enhan. No. = %d\n', NumFea, NumWin, NumEnhan);
[train_rate,test_rate,C_train_rate,NetoutTrain,NetoutTest] = GRBLS_train(train_x,train_y,contaminated_train_y,test_x,test_y,lambda1,lambda2,WF,WeightEnhan,NumFea,NumWin,NN,options);
result = [result;NumEnhan, train_rate, test_rate, C_train_rate];
if test_rate > best_test
best_test = test_rate;
load('C_id.mat');
save(fullfile(file_name_1,['contamination_proportion ', num2str(prop), ' best_result.mat']),'best_test','train_rate','C_train_rate','NumFea','NumWin','NumEnhan','lambda1','lambda2','k',...
'train_x','train_y','test_x','test_y','contaminated_train_y','NetoutTrain','NetoutTest','C_id','prop');
end
clearvars -except train_x train_y test_x test_y lambda1 lambda2 WF WeightEnhan NumFea NumWin NumEnhan NN best_test experiment_num ...
k result file_name file_name_1 contaminated_train_y prop options
end
result_plot(result,file_name);
clear result
result = [];
end
end
experiment_num=experiment_num+1;
save('num.mat','experiment_num');EuDIst.m calculates the Euclidean distance,
constraintW.m generates W. alas, this is the code written by others. I don't remember where I found it.
Just sew it up. Then I wrote the function of plot, drew the change trend and added the function of pollution.
shuffle_index.m
rng('shuffle');
x = x';
gross = train_num + test_num ;
category_box = unique(y);
category_box = sort(category_box);
category = size(category_box,1);
category_rule = zeros(category, category);
for i=1:category
category_rule(i,i)=1;
end
save('category_map.mat','category','category_box','category_rule')
len = size(y);
rand_id = randperm(len(1));
train_x = x(:, rand_id(1:train_num));
train_y = y(rand_id(1:train_num), :);
test_x = x(:, rand_id(train_num+1:gross));
test_y = y(rand_id(train_num+1:gross), :);
[train_x, PS] = mapminmax(train_x);
test_x = mapminmax('apply', test_x, PS);
train_x = train_x';
test_x = test_x';
train_y1 = zeros(size(train_y, 1), category);
test_y1 = zeros(size(test_y, 1), category);
NN.train = zeros(1,category); % number of two category
NN.test = zeros(1,category);
for i=1:size(train_y, 1)
for j=1:category
if train_y(i, 1) == category_box(j, 1)
train_y1(i, j) = 1;
NN.train(1,j) = NN.train(1,j)+1;
end
end
end
for i=1:size(test_y, 1)
for j=1:category
if test_y(i, 1) == category_box(j, 1)
test_y1(i, j) = 1;
NN.test(1,j) = NN.test(1,j)+1;
end
end
end
train_y = train_y1;
test_y = test_y1;
contaminate_label.m:
total = sum(NN);
contamination_num = ceil(proportion * total);
C_id = randperm(total);
new_y = zeros(size(y));
new_y(C_id(contamination_num+1:total),:) = y(C_id(contamination_num+1:total),:);
load('category_map.mat');
for i = 1:contamination_num
j = find(y(C_id(i), :) == max(y(C_id(i), :))); %1
pol_label = randperm(category); %1,2 2,1
if pol_label(1) ~= j
new_y(C_id(i),:) = category_rule(pol_label(1),:);
else
new_y(C_id(i),:) = category_rule(pol_label(2),:);
end
end
contaminated_y = new_y;Partial code of plot:
fig1=figure;
set(fig1,'visible','off');
set(0, 'currentFigure', fig1);
plot(result(:,1),result(:,2),'-vr');
hold on;
plot(result(:,1),result(:,3),'-^b');
legend('training_sample', 'testing_sample' );
xlabel('\itenhancement nodes','FontSize',12);ylabel('\itrate','FontSize',12);
frame = getframe(fig1);
im = frame2im(frame);
pic_name=fullfile(file_name,['rate_comparion','.png']);
imwrite(im,pic_name);
close all;It seems that the data downloaded from UCI cannot be used directly. For example, if there is something missing, it is generally filtered in python and then saved directly in matlab:
python:
import csv
import re
f = open(".txt",encoding='utf-8')
f_new = open('new.txt','w')
line = f.readline()
Nan_num=0
num=0
i=0
while line:
c=re.search('\?',line)
if bool(c):
Nan_num += 1
else:
num += 1
f_new.write(line)
line = f.readline()
i=i+1
if i>1000:
line=''
f_new.close()
f.close() matlab:
sample=importdata('.txt');
x=sample(:,1:);
y=sample(:,);
save('.mat','x','y')