Introduction: _Using the basic functions in Paddle, ordinary linear and Logistic regression problems, especially the observation of the structure of network coefficients, are designed, which can then be used to modify the network.
Keywords: Paddle, Linear Regression, Logistics
_01 Basic Operations
_Tensor is the basic unit of operation under Paddle. This has more properties than the normal number, numpy matrix, such as shape, dtype, stop_gradient, etc.
1.1 Declare Tensor
_Using some initialization functions of paddle, it is easier to directly produce some special Tensor s.
_Below are all the properties of paddle, where ones, zeros, can be used to declare Tensor.
CPUPlace CUDAPinnedPlace CUDAPlace DataParallel Model ParamAttr Tensor XPUPlace __builtins__ __cached__ __doc__ __file__ __git_commit__ __loader__ __name__ __package__ __path__ __spec__ __version__ abs acos add add_n addmm all allclose amp any arange argmax argmin argsort asin assign atan batch bernoulli bmm broadcast_shape broadcast_to callbacks cast ceil cholesky chunk clip common_ops_import compat concat conj cos cosh create_parameter crop cross cumsum dataset device diag disable_static dist distributed distribution divide dot empty empty_like enable_static equal equal_all erf exp expand expand_as eye flatten flip floor floor_divide floor_mod flops fluid framework full full_like gather gather_nd get_cuda_rng_state get_cudnn_version get_default_dtype get_device grad greater_equal greater_than hapi histogram imag in_dynamic_mode increment incubate index_sample index_select inverse io is_compiled_with_cuda is_compiled_with_xpu is_empty is_tensor isfinite isinf isnan jit kron less_equal less_than linspace load log log10 log1p log2 logical_and logical_not logical_or logical_xor logsumexp masked_select matmul max maximum mean median meshgrid metric min minimum mm mod monkey_patch_math_varbase monkey_patch_variable multinomial multiplex multiply mv nn no_grad nonzero norm normal not_equal numel ones ones_like onnx optimizer os paddle pow prod rand randint randn randperm rank reader real reciprocal regularizer remainder reshape reshape_ reverse roll round rsqrt save scale scatter scatter_ scatter_nd scatter_nd_add seed set_cuda_rng_state set_default_dtype set_device set_printoptions shape shard_index sign sin sinh slice sort split sqrt square squeeze squeeze_ stack standard_normal stanh static std strided_slice subtract sum summary sysconfig t tanh tanh_ tensor text tile to_tensor topk trace transpose tril triu unbind uniform unique unsqueeze unsqueeze_ unstack utils var
1.1. 1 Declare Tensor
x1 = paddle.zeros([2,2], dtype='int64') x2 = paddle.ones([2,2], dtype='float64') x3 = x1 + x2 print(x3)
Tensor(shape=[2, 2], dtype=int64, place=CPUPlace, stop_gradient=True,
[[1, 1],
[1, 1]])
_From the results above, for different data types (float64, int64), the final result is converted to the type of int64.
_02 Linear Regression
2.1 Defining a data model
_We use numpy to define a set of data, 13 of which are each, and for example, all but the first number is filled with 0. This set of data is y = 2 * x + 1, but the program is unknown. We then use this set of data to train to see if a strong neural network can train a model to fit this function. Finally, a prediction data is defined, which is used as the X-input at the end of the training to see if the predictions are close to the correct values.
2.1. 1 Builder Function
x_data = array([[i]+[0]*12 for i in range(1,6)]).astype('float32')
y_data = array([[i*2+1] for i in range(1,6)]).astype('float32')
test_data = array([[6]+[0]*12]).astype('float32')
print(x_data, "\n", y_data, "\n", test_data)
2.1. 2 Build results
x_data = array([[i]+[0]*12 for i in range(1,6)]).astype('float32')
y_data = array([[i*2+1] for i in range(1,6)]).astype('float32')
test_data = array([[6]+[0]*12]).astype('float32')
print(x_data, "\n\n", y_data, "\n\n", test_data)
[[1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[2. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[3. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[4. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[5. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
[[ 3.]
[ 5.]
[ 7.]
[ 9.]
[11.]]
[[6. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
2.2 Building Linear Networks
2.2. 1 Network Structure
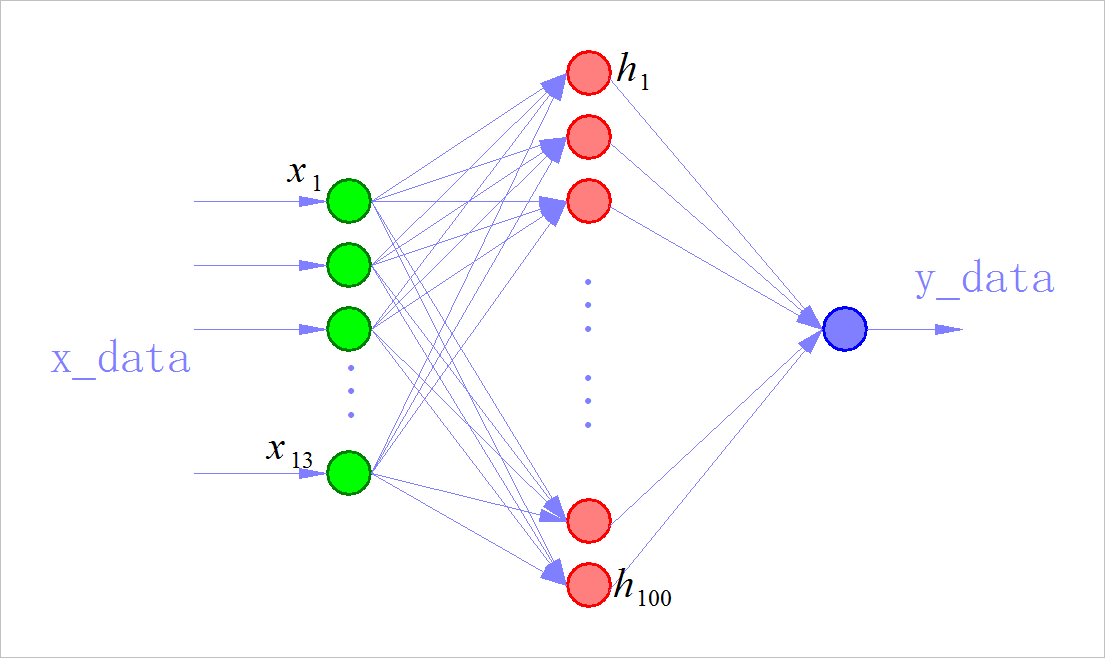
_Defines a simple linear network, which is very simple and structured as:
[Input Layer][Hidden Layer][Activation Function][Output Layer]
_More specifically, a fully connected layer with an output size of 100, followed by an activation function ReLU and a fully connected layer with an output size of 1, constructs a very simple network.
_The shape of the input layer is defined here as 13, because each data in the Boston House Price Data Set has 13 attributes, and the datasets we customize later are designed to fit this dimension.
2.2. 2 Define a linear network
(1) Network structure
net = paddle.nn.Sequential(
paddle.nn.Linear(13,100),
paddle.nn.ReLU(),
paddle.nn.Linear(100,1),
)
optimizer = paddle.optimizer.SGD(learning_rate=0.01, parameters=net.parameters())
_Next comes the definition of the optimization method used in training, where the random gradient descent optimization method is used. PaddlePaddle provides a number of optimization function interfaces. In addition to the random gradient descent (SGD) method used in this project, Momentum, Adagrad, Adagrad, and so on, readers can use different optimization methods for their own project needs.
(2) Define the loss function
_Because this project is a linear regression task, we used the Square Difference Loss function in our training. Because paddle. Nn. Function. Square_ Error_ Cost is asking for a Batch loss, so we're also asking for an average. PaddlePaddle provides many interfaces for loss functions, such as the cross-entropy loss function paddle.nn.CrossEntropyLoss.
_During the training process, we can see that the output loss value is decreasing, which proves that our model is convergent.
import paddle import paddle.nn.functional as F from paddle import to_tensor as TT from paddle.nn.functional import square_error_cost as sqrc
net = paddle.nn.Sequential(
paddle.nn.Linear(13,100),
paddle.nn.ReLU(),
paddle.nn.Linear(100,1),
)
optimizer = paddle.optimizer.SGD(learning_rate=0.01, parameters=net.parameters())
inputs = TT(x_data)
labels = TT(y_data)
for pass_id in range(10):
out = net(inputs)
loss = paddle.mean(sqrc(out, labels))
loss.backward()
optimizer.step()
optimizer.clear_grad()
print("pass: %d, Cost:%0.5f"%(pass_id, loss))
pass: 0, Cost:71.86705
pass: 1, Cost:30.57855
pass: 2, Cost:11.62621
pass: 3, Cost:1.53674
pass: 4, Cost:0.02941
pass: 5, Cost:0.01128
pass: 6, Cost:0.01104
pass: 7, Cost:0.01081
pass: 8, Cost:0.01058
pass: 9, Cost:0.01036
_After the training, we used the forecasting program obtained from the cloning main program above to predict the forecasting data that we just defined. When we define the data above, the rule y = 2 * x + 1 is satisfied, so when x is 6, y should be 13, and the final output should be close to 13.
2.2. 3 Network Prediction
predict_inputs = TT(test_data)
result = net(predict_inputs)
print('x=%0.3f, y=%0.5f'%(test_data.flatten()[0], result))
x=6.000, y=13.15371
2.3 Network parameters
Where are the parameters of the linear model ahead?
2.3. 1 All parameter types
parms = net.parameters() print(type(parms)) print(len(parms)) _=[print(type(parms[i])) for i in range(len(parms))]
<class 'list'>
4
<class 'paddle.fluid.framework.ParamBase'>
<class 'paddle.fluid.framework.ParamBase'>
<class 'paddle.fluid.framework.ParamBase'>
<class 'paddle.fluid.framework.ParamBase'>
2.3. 2 First parameter
_The first parameter is the matrix input to the hidden layer, shape = (13,10)
print(parms[0].numpy())
[[-0.075387 0.5339514 -0.5040579 0.21901496 0.34557822 -0.11829474
-0.00709895 0.37773132 0.8291067 0.7896065 ]
[ 0.2871285 -0.43426144 -0.15709287 -0.1772753 0.00291133 0.097902
0.03845656 -0.20523474 -0.37873447 0.09981477]
[ 0.10757929 -0.01285398 -0.24694431 0.07925624 -0.18733147 0.08271486
0.37385654 -0.22516277 0.29894334 -0.49872464]
[ 0.31193787 0.27885395 -0.3627605 0.116359 -0.06722078 -0.33219916
0.27342808 -0.24131414 0.42575645 0.05287254]
[-0.4429462 -0.2931974 0.09456986 -0.2963 -0.3600033 -0.24172312
0.05790824 -0.28486678 -0.44249436 0.13542217]
[ 0.49579376 -0.3068263 0.4475448 -0.21869034 -0.22201723 0.14771122
-0.26021212 -0.49464276 -0.0877367 -0.22605684]
[ 0.43755406 -0.43096933 0.3386714 -0.28694224 -0.03674829 0.39764756
-0.3881266 0.35218292 0.00819886 0.04092628]
[ 0.26412088 -0.05456609 -0.25517958 0.01412582 0.29454744 -0.3844456
0.24271363 0.26424062 0.35327762 0.39541048]
[-0.0133011 0.24380505 0.42668605 -0.19451535 -0.31308573 0.33640432
0.40896732 0.13685054 0.38675517 -0.06989819]
[ 0.13358372 -0.36512688 0.06258923 -0.29652268 0.29847944 0.04026729
-0.23680806 -0.13740104 0.40020412 0.50566524]
[-0.47494102 -0.32276535 -0.03033391 -0.33728325 0.32518142 -0.31474313
0.24827117 -0.42601836 -0.44340318 -0.3654582 ]
[-0.09328851 -0.48388985 -0.16385913 -0.18592414 0.06326699 -0.4801174
0.48408395 0.20635891 0.14444119 0.08807671]
[ 0.21163589 -0.02607039 0.36036986 -0.11807913 -0.2828287 0.23282737
-0.23758212 -0.41061205 0.1697821 0.25588465]]
2.3. 3Second parameter
_The second parameter is the offset of all cryptogenic neurons, shape=(1,10)
print(parms[1].numpy())
[ 0. 0.04476326 0. 0.04997304 -0.00701768 -0.07669634
-0.01661819 0.10008517 0.1378215 0.12973393]
2.3. 4 Third parameter
_The third parameter outputs the weights of the neurons in the form of (10,1)
print(parms[2].numpy())
[[-0.54290414]
[ 0.4281348 ]
[ 0.6710895 ]
[ 0.3250693 ]
[ 0.10694236]
[-0.6338133 ]
[-0.1300693 ]
[ 0.626347 ]
[ 0.9877776 ]
[ 0.93352455]]
2.3. 5Fourth parameter
The fourth parameter is the offset of the output neuron:
print(parms[3].numpy())
[0.17823167]
2.4 Network Performance
2.4. 1 Input and Output
td2 = TT(array([[i]+[0]*12 for i in linspace(0,10,100)]).astype('float32'))
prd2 = net(td2)
plt.figure(figsize=(8,5))
plt.plot(td2.numpy().T[0], prd2.numpy().T[0])
plt.xlabel("inputs")
plt.ylabel("outputs")
plt.grid(True)
plt.tight_layout()
plt.show()
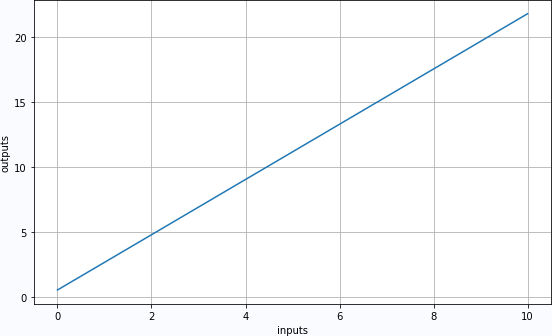
2.4.2 LMS estimates W,b
x = td2.numpy().T[0]
y = prd2.numpy().T[0]
W = linalg.inv(dot(x[:,newaxis],x[newaxis,:])+eye(len(y))*0.1).dot(x).dot(y)
B = mean(y-W*x)
print('W:%0.5f'%W, "\n", 'b:%0.5f'%B)
W:2.20889
b:0.13555
_03 Logistic Regression
3.1 Network Definition
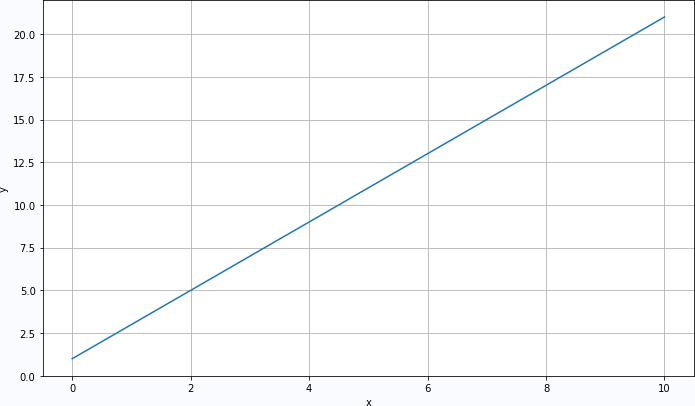
Increase data volume:
t = linspace(0, 10, 100)
x_data = array([[i]+[0]*12 for i in t]).astype('float32')
y_data = array([[i*2+1] for i in t]).astype('float32')
test_data = array([[6]+[0]*12]).astype('float32')
plt.plot(t, y_data.flatten())
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
plt.tight_layout()
plt.show()
#------------------------------------------------------------
net = paddle.nn.Sequential(
paddle.nn.Linear(13,200),
paddle.nn.Sigmoid(),
paddle.nn.Linear(200,1),
)
optimizer = paddle.optimizer.SGD(learning_rate=0.005, parameters=net.parameters())
inputs = TT(x_data)
labels = TT(y_data)
for pass_id in range(10000):
out = net(inputs)
loss = paddle.mean(sqrc(out, labels))
loss.backward()
optimizer.step()
optimizer.clear_grad()
if pass_id % 1000 == 0:
print("pass: %d, Cost:%0.5f"%(pass_id, loss))
3.2 Training Result
3.2. 1 Input data
3.2. 2 Training process
pass: 0, Cost:163.94566
pass: 1000, Cost:0.14547
pass: 2000, Cost:0.08274
pass: 3000, Cost:0.05948
pass: 4000, Cost:0.04697
pass: 5000, Cost:0.03904
pass: 6000, Cost:0.03352
pass: 7000, Cost:0.02943
pass: 8000, Cost:0.02627
pass: 9000, Cost:0.02374
3.2. 3 Prediction results
td2 = TT(array([[i]+[0]*12 for i in linspace(0,10,100)]).astype('float32'))
prd2 = net(td2)
plt.figure(figsize=(8,5))
plt.plot(td2.numpy().T[0], prd2.numpy().T[0])
plt.xlabel("inputs")
plt.ylabel("outputs")
plt.grid(True)
plt.tight_layout()
plt.show()
#------------------------------------------------------------
x = td2.numpy().T[0]
y = prd2.numpy().T[0]
W = linalg.inv(dot(x[:,newaxis],x[newaxis,:])+eye(len(y))*0.1).dot(x).dot(y)
B = mean(y-W*x)
print('W:%0.5f'%W, "\n", 'b:%0.5f'%B)
3.2. 4 Forecast results
td2 = TT(array([[i]+[0]*12 for i in linspace(0,10,100)]).astype('float32'))
prd2 = net(td2)
plt.figure(figsize=(10,6))
plt.plot(td2.numpy().T[0], prd2.numpy().T[0])
plt.xlabel("inputs")
plt.ylabel("outputs")
plt.grid(True)
plt.tight_layout()
plt.show()
#------------------------------------------------------------
x = td2.numpy().T[0]
y = prd2.numpy().T[0]
W = linalg.inv(dot(x[:,newaxis],x[newaxis,:])+eye(len(y))*0.1).dot(x).dot(y)
B = mean(y-W*x)
print('W:%0.5f'%W, "\n", 'b:%0.5f'%B)
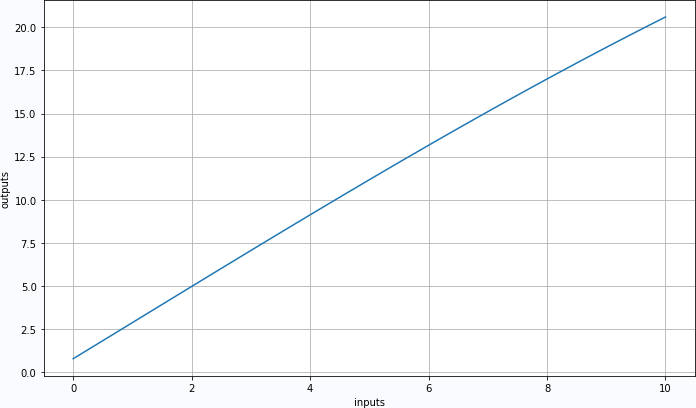
_Linear parameter results:
W:2.14812
b:0.25936
_total_knot_
_Using the basic functions in Paddle, ordinary linear and Logistic regression problems, especially the observation of the structure of network coefficients, are designed, which can then be used to modify the network.
Related chart links: