1, Introduction
1 origin and development of ant colony algorithm (ACA)
In the process of studying the new algorithm, Marco Dorigo and others found that when ant colony is looking for food, they can exchange foraging information by secreting a biological hormone called pheromone, so they can quickly find the target. Therefore, in their doctoral thesis in 1991, they systematically proposed a new intelligent optimization algorithm "Ant system (AS) based on ant population for the first time. Later, The proposer and many researchers have made various improvements to the algorithm and applied it to a wider range of fields, such AS graph coloring problem, quadratic assignment problem, workpiece scheduling problem, vehicle routing problem, job shop scheduling problem, network routing problem, large-scale integrated circuit design and so on. In recent years, M.Dorigo and others have further developed ant algorithm into a general optimization technology "Ant Colony Optimization (ACO)", and called all algorithms in line with ACO framework "ACO algorithm".
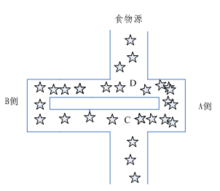
Specifically, each ant starts looking for food without telling where the food is in advance. When one finds food, it will release a volatile secretion pheromone (called pheromone, which will gradually volatilize and disappear over time. The pheromone concentration represents the distance of the path). Pheromone can be perceived by other ants and play a guiding role. Usually, when there are pheromones on multiple paths, ants will preferentially choose the path with high pheromone concentration, so that the pheromone concentration of the path with high concentration is higher, forming a positive feedback. Some ants do not always repeat the same path as other ants. They will find another way. If the other path is shorter than the original one, then gradually, more ants are attracted to this shorter path. Finally, after a period of operation, the shortest path may be repeated by most ants. Finally, the path with the highest pheromone concentration is the optimal path finally selected by ants.
Compared with other algorithms, ant colony algorithm is a relatively young algorithm, which has the characteristics of distributed computing, no central control, asynchronous and indirect communication between individuals, and is easy to be combined with other optimization algorithms. After the continuous exploration of many people with lofty ideals, a variety of improved ant colony algorithms have been developed today, but the principle of ant colony algorithm is still the backbone.
2. Solution principle of ant colony algorithm
Based on the above description of ant colony foraging behavior, the algorithm mainly simulates the foraging behavior in the following aspects:
(1) The simulated graph scene contains two pheromones, one represents home and the other represents the location of food, and both pheromones are volatilizing at a certain rate.
(2) Each ant can only perceive information in a small part of its surroundings. When ants are looking for food, if they are within the perceptual range, they can go directly. If they are not within the perceptual range, they should go to the place with more pheromones. Ants can have a small probability not to go to the place with more pheromones and find another way. This small probability event is very important, which represents an innovation in finding a way and is very important for finding a better solution.
(3) The rules for ants to return to their nest are the same as those for finding food.
(4) When moving, the ant will first follow the guidance of pheromone. If there is no guidance of pheromone, it will go inertia according to its moving direction, but there is also a certain chance to change the direction. The ant can also remember the road it has traveled and avoid going to one place again.
(5) Ants leave the most pheromones when they find food, and then the farther away from the food, the less pheromones they leave. The rules for finding the amount of pheromone left in the nest are the same as those of food. Ant colony algorithm has the following characteristics: positive feedback algorithm, concurrency algorithm, strong robustness, probabilistic global search, independent of strict mathematical properties, long search time and easy to stop.
Ant transfer probability formula:
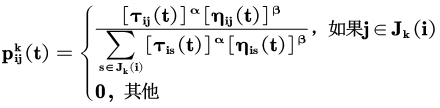
In the formula: is the probability of ant k transferring from city i to j; α,β The relative importance of pheromones and heuristic factors; Is the pheromone quantity on edge (i,j); Is heuristic factor; Select the city allowed for ant k next step. The above formula is the pheromone update formula in ant system, which is the amount of pheromone on edge (i,j); ρ The evaporation coefficient is 0< ρ< 1; Is the pheromone quantity of the kth ant left on the edge (i,j) in this iteration; Q is a normal coefficient; Is the path length of the kth ant in this tour.
In ant system, pheromone update formula is:
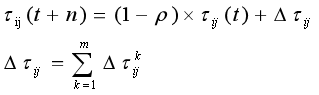
3. Solving steps of ant colony algorithm:
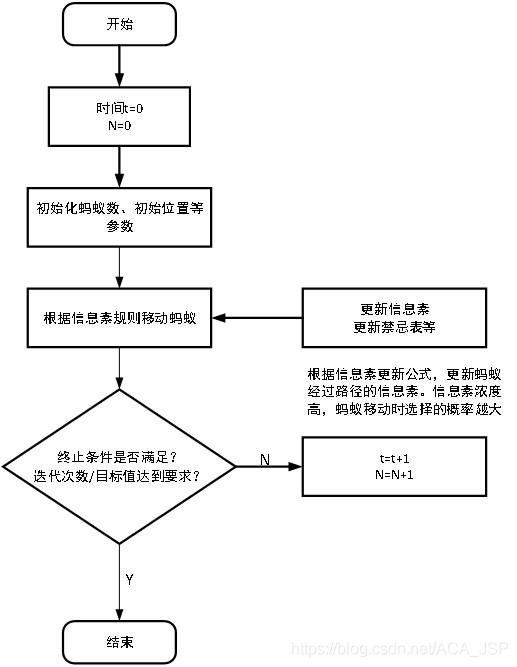
(1) Initialization parameters at the beginning of calculation, relevant parameters need to be initialized, such as ant colony size (number of ants) m and pheromone importance factor α, Heuristic function importance factor β, Pheromone will send Silver ρ, Total pheromone release Q, maximum number of iterations iter_max, initial value of iteration times iter=1.
(2) The solution space is constructed. Each ant is randomly placed at different starting points. For each ant K (k=1,2,3... m), the next city to be visited is calculated according to (2-1) until all ants have visited all cities.
(3) Update the information, calculate the path length Lk(k=1,2,..., m) of each ant, and record the optimal solution (shortest path) in the current number of iterations. At the same time, the pheromone concentration on each urban connection path is updated according to equations (2-2) and (2-3).
(4) Judge whether to terminate if ITER < ITER_ Max, then make iter=iter+1, clear the record table of ant passing path, and return to step 2; Otherwise, the calculation is terminated and the optimal solution is output.
(5) Judge whether to terminate if ITER < ITER_ Clear the path of the ant and return to the record table of ITER + max = 1; Otherwise, the calculation is terminated and the optimal solution is output. 3. Judge whether to terminate if ITER < ITER_ Max, then make iter=iter+1, clear the record table of ant passing path, and return to step 2; Otherwise, the calculation is terminated and the optimal solution is output.
2, Source code
clear
clc
close all
tic
%% use importdata This function reads the file
c101=importdata('c101.txt');
cap=200; %Maximum vehicle load
%% Extract data information
E=c101(1,5); %Start time of distribution center time window
L=c101(1,6); %End time of distribution center time window
vertexs=c101(:,2:3); %Coordinates of all points x and y
customer=vertexs(2:end,:); %Customer coordinates
cusnum=size(customer,1); %Number of customers
v_num=25; %Maximum number of vehicles used
demands=c101(2:end,4); %requirement
a=c101(2:end,5); %Customer time window start time[a[i],b[i]]
b=c101(2:end,6); %End time of customer time window[a[i],b[i]]
width=b-a; %Customer time window width
s=c101(2:end,7); %Customer service time
h=pdist(vertexs);
dist=squareform(h); %Distance matrix
%% Initialization parameters
m=50; %Ant number
alpha=1; %Pheromone importance factor
beta=3; %Heuristic function importance factor
gama=2; %Waiting time importance factor
delta=3; %Time window span importance factor
r0=0.5; %r0 Is the parameter used to control the transition rule
rho=0.85; %Pheromone volatilization factor
Q=5; %Update the constant of pheromone concentration
Eta=1./dist; %Heuristic function
Tau=ones(cusnum+1,cusnum+1); %Pheromone matrix
Table=zeros(m,cusnum); %Path record form
iter=1; %Initial value of iteration times
iter_max=30; %Maximum number of iterations
Route_best=zeros(iter_max,cusnum); %Best path of each generation
Cost_best=zeros(iter_max,1); %Cost of the best path of each generation
%% Iterative search for the best path
while iter<=iter_max
%% First build the path of all ants
%Ant by ant selection
for i=1:m
%Customer by customer selection
for j=1:cusnum
r=rand; %r For in[0,1]Random variables on
np=next_point(i,Table,Tau,Eta,alpha,beta,gama,delta,r,r0,a,b,width,s,L,dist,cap,demands);
Table(i,j)=np;
end
end
%% Calculate the cost of each ant=1000*Number of vehicles used+Total vehicle distance
cost=zeros(m,1);
NV=zeros(m,1);
TD=zeros(m,1);
for i=1:m
VC=decode(Table(i,:),cap,demands,a,b,L,s,dist);
[cost(i,1),NV(i,1),TD(i,1)]=costFun(VC,dist);
end
%% Calculate minimum cost and average cost
if iter == 1
[min_Cost,min_index]=min(cost);
Cost_best(iter)=min_Cost;
Route_best(iter,:)=Table(min_index,:);
else
[min_Cost,min_index]=min(cost);
Cost_best(iter)=min(Cost_best(iter - 1),min_Cost);
if Cost_best(iter)==min_Cost
Route_best(iter,:)=Table(min_index,:);
else
Route_best(iter,:)=Route_best((iter-1),:);
end
end
%% Find the ant according to the transfer formula k from i Point of departure moves to the next point j,j The point must satisfy the capacity and time constraints and be not used k Served customers
function j=next_point(k,Table,Tau,Eta,alpha,beta,gama,delta,r,r0,a,b,width,s,L,dist,cap,demands)
route_k=Table(k,:); %Ants k Path of
i=route_k(find(route_k~=0,1,'last')); %Ants k Customer number being accessed
if isempty(i)
i=0;
end
route_k(route_k==0)=[]; %Remove 0 from ant k Deleted from the path record array
cusnum=size(Table,2); %Number of customers
allSet=1:cusnum; %setxor(a,b)Can get a,b Elements that are different from two matrices are also called elements that are not in the intersection set,
unVisit=setxor(route_k,allSet); %Find the ant k Collection of unserved customers
uvNum=length(unVisit); %Find the ant k Number of unserved customers
[VC,NV,TD]=decode(route_k,cap,demands,a,b,L,s,dist); %Ants k All paths built so far
%If the current delivery path is empty
if ~isempty(VC)
route=VC{end,1}; %Ants k Path currently being built
else
%If the current route distribution scheme is not empty
route=[];
end
lr=length(route); %Ants k Number of customers visited by the path currently being built
preroute=zeros(1,lr+1); %Temporary variables, storing ants k The path currently being built is the path after adding the next point
preroute(1:lr)=route;
Nik=next_point_set(k,Table,cap,demands,a,b,L,s,dist); %Find ants k from i Point of departure can be moved to the next point j A collection of, j The point must meet the capacity and time constraints and be not affected by ants k Served customers
%% If r<=r0,j=max{[Tau(i,j)]^alpha * [Eta(i+1,j+1)]^beta * [1/width(j)]^gama * [1/wait(j)]^delta}
if r<=r0
%If Nik Not empty, that is, ants k You can select a customer from the current path i Continue to visit customers
if ~isempty(Nik)
Nik_num=length(Nik);
p_value=zeros(Nik_num,1); %Record state transition probability
for h=1:Nik_num
j=Nik(h);
preroute(end)=j;
[~,~,wait,~]=begin_s(preroute,a,s,dist);
if wait(end)==0
wait(end)=1e-8;
end
p_value(h,1)=((Tau(i+1,j+1))^alpha)*((Eta(i+1,j+1))^beta)*((1/width(j))^gama)*((1/wait(end))^delta);
end
[~,maxIndex]=max(p_value); %find p_value Sequence number of the maximum value in
j=Nik(maxIndex); %Identify customers j
else
%If Nik Empty, i.e. ant k You must return to the distribution center and visit new customers from the distribution center
p_value=zeros(uvNum,1); %Record state transition probability
for h=1:uvNum
j=unVisit(h);
preroute(end)=j;
[~,~,wait,~]=begin_s(preroute,a,s,dist);
if wait(end)==0
wait(end)=1e-8;
end
p_value(h,1)=((Tau(i+1,j+1))^alpha)*((Eta(i+1,j+1))^beta)*((1/width(j))^gama)*((1/wait(end))^delta);
end
[~,maxIndex]=max(p_value); %find p_value Sequence number of the maximum value in
j=unVisit(maxIndex); %Identify customers j
end
else
%% If r>r0,Select points by roulette method according to probability formula j
%If Nik Not empty, that is, ants k You can select a customer from the current path i Continue to visit customers
if ~isempty(Nik)
Nik_num=length(Nik);
p_value=zeros(Nik_num,1); %Record state transition probability
for h=1:Nik_num
j=Nik(h);
preroute(end)=j;
[~,~,wait,~]=begin_s(preroute,a,s,dist);
if wait(end)==0
wait(end)=1e-8;
end
p_value(h,1)=((Tau(i+1,j+1))^alpha)*((Eta(i+1,j+1))^beta)*((1/width(j))^gama)*((1/wait(end))^delta);
end
index=roulette(p_value); %Select the serial number according to roulette
j=Nik(index); %Identify customers j
else
%If Nik Empty, i.e. ant k You must return to the distribution center and visit new customers from the distribution center
p_value=zeros(uvNum,1); %Record state transition probability
for h=1:uvNum
j=unVisit(h);
preroute(end)=j;
[~,~,wait,~]=begin_s(preroute,a,s,dist);
if wait(end)==0
wait(end)=1e-8;
end
p_value(h,1)=((Tau(i+1,j+1))^alpha)*((Eta(i+1,j+1))^beta)*((1/width(j))^gama)*((1/wait(end))^delta);
end
3, Operation results
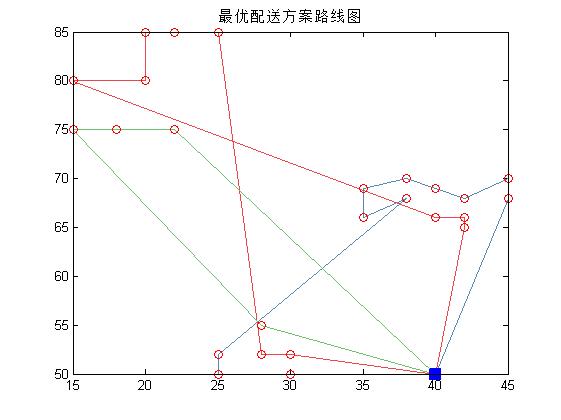
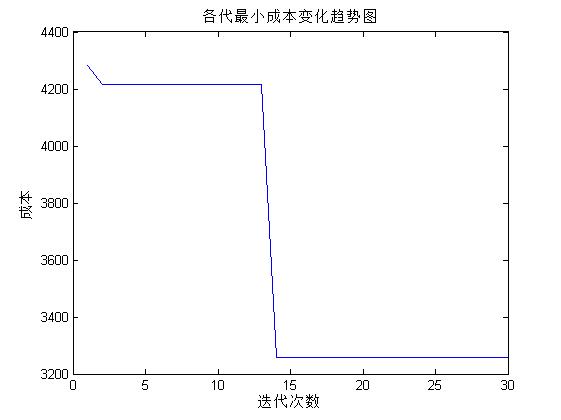
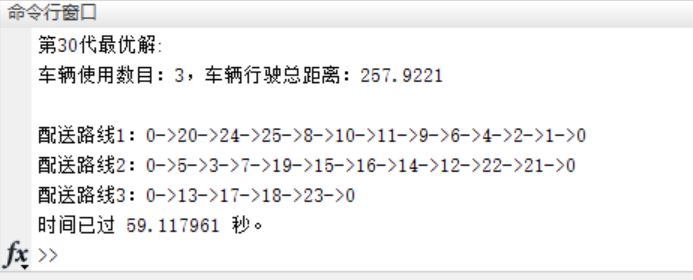
4, Remarks
Version: 2014a
Complete code or write on behalf of QQ912100926