1, Quaternion common API s
Quaternion.FromToRotation(Vector3 fromDirection, Vector3 toDirection)
Official analysis: creates a rotation which revolutions from fromdirection to todirection
Create a rotation from the form direction to the target direction
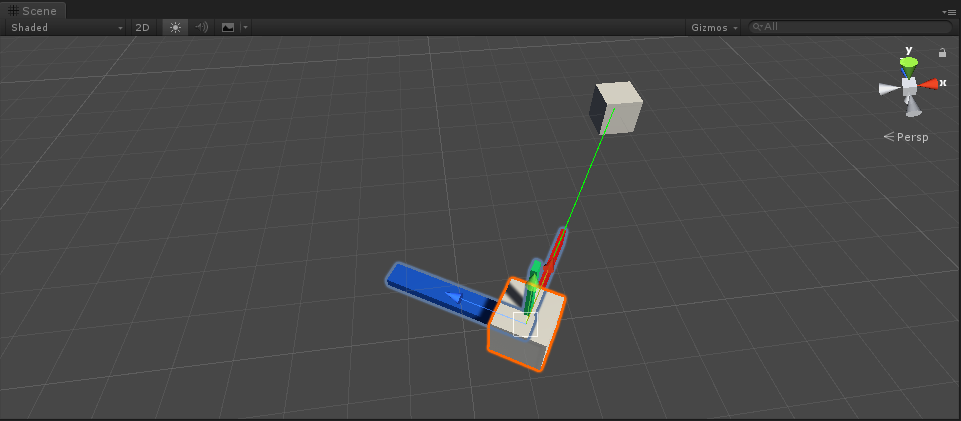
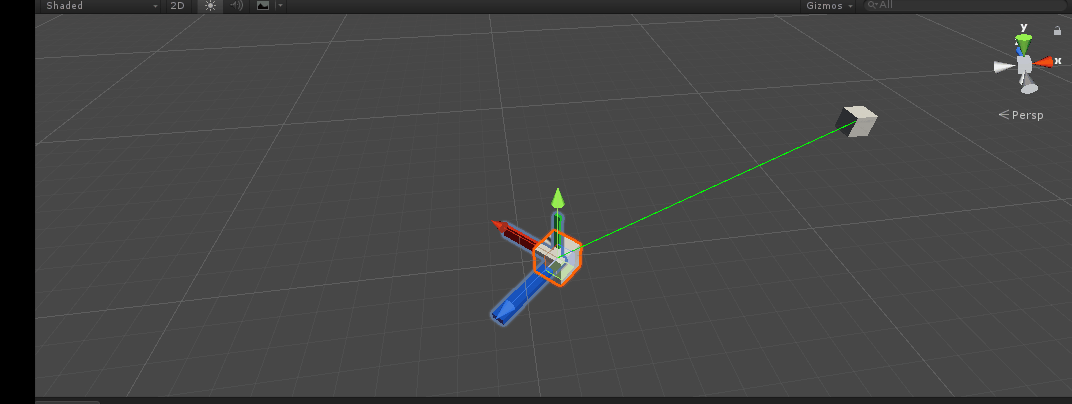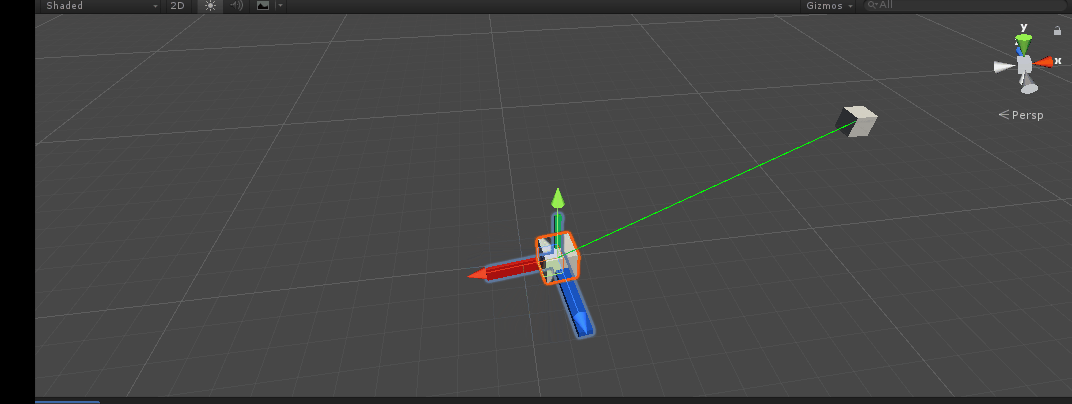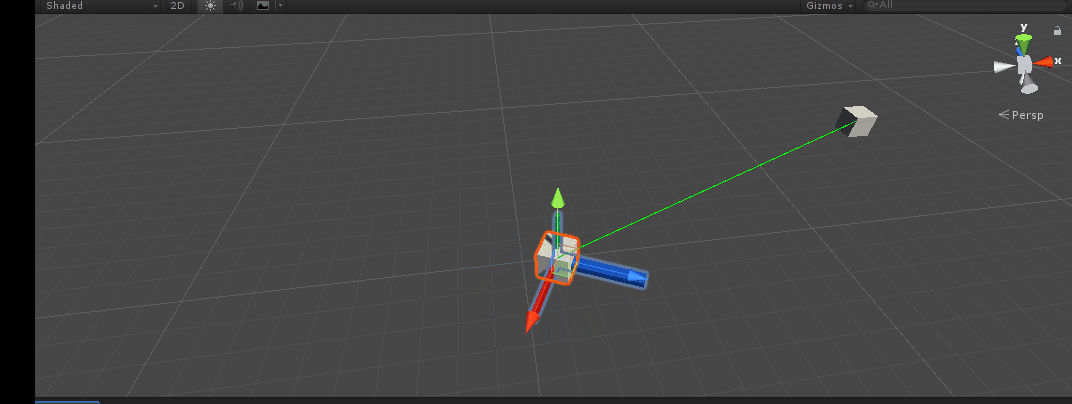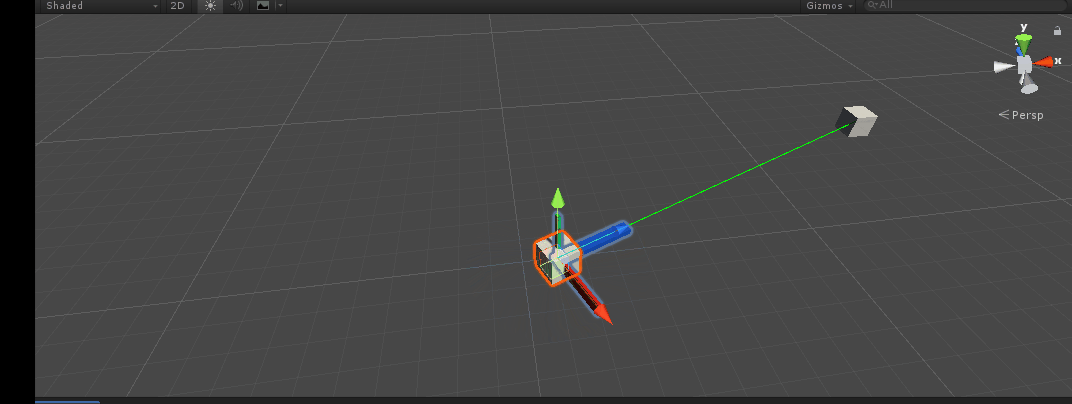
Imagine a scenario like this. Let's use quaternion From torotation() API, what should I do to orient the z axis (blue axis) of the main object (m_MainTran) in the following figure towards the target object (m_TargetTran).
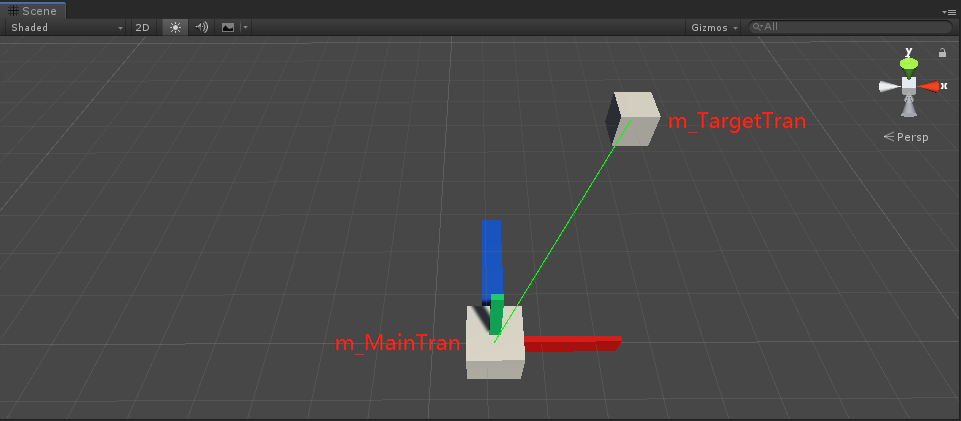
code
//Find the target orientation
Vector3 targetDir = m_TargetTran.position - m_MainTran.position;
//Find m_MainTran.forward the rotation quaternion required to rotate to the target direction
Quaternion q = Quaternion.FromToRotation(m_MainTran.forward, targetDir);
//Apply the calculated rotation quaternion to the forward direction
Vector3 finalDir = q * m_MainTran.forward;
//Finally, make the forward of the main target towards the calculated direction
m_MainTran.forward = finalDir;
The parsing is annotated. Next, let's see the effect
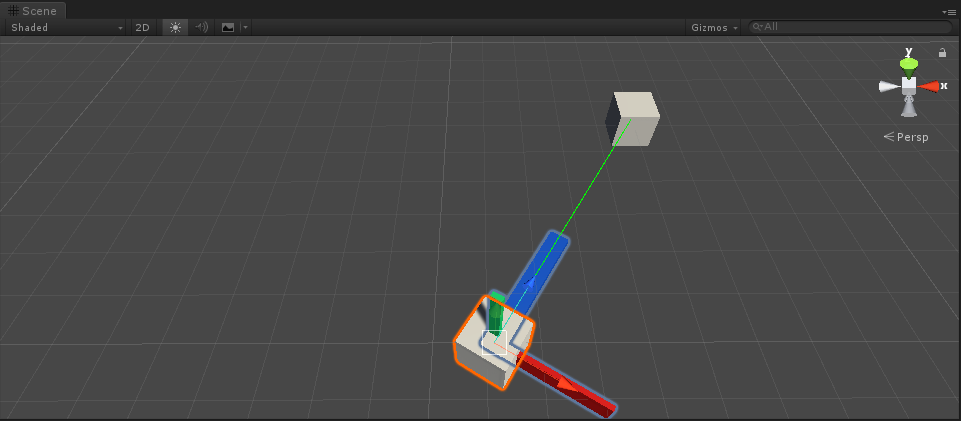
Similarly, if we want the x-axis of the main target to face the target, that is, the right direction. It can be written like this
//Find the target orientation
Vector3 targetDir = m_TargetTran.position - m_MainTran.position;
//Find m_MainTran.right the rotation quaternion required to rotate to the target direction
Quaternion q = Quaternion.FromToRotation(m_MainTran.right,targetDir);
//Apply the calculated rotation quaternion to the right direction
Vector3 finalDir = q * m_MainTran.right;
//Finally, make the right of the main target face the calculated direction
m_MainTran.right = finalDir;
design sketch
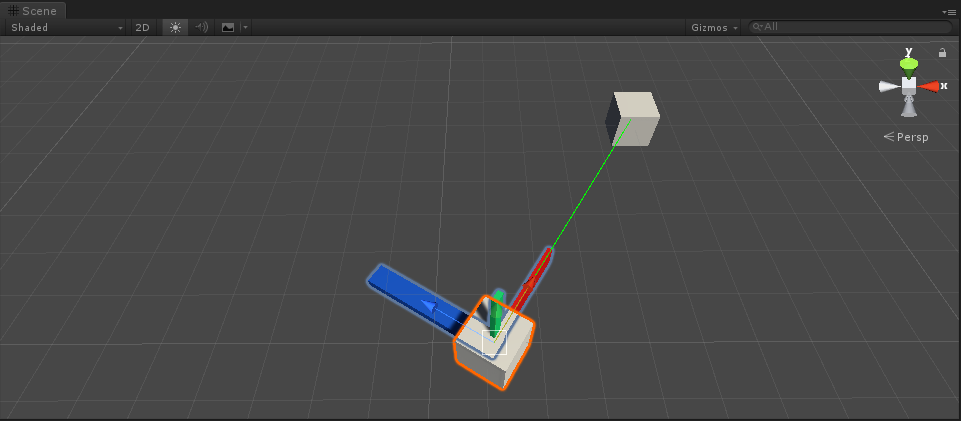
This is useful in 2D games. Because in 2D games, we usually make the x or y of the object face the target, not the z axis
Quaternion.LookRotation(Vector3 forward, Vector3 upwards = Vector3.up)
- Official analysis: creates a rotation with the specified forward and upward directions
- Create a rotation. Make the positive direction of the target (z-axis) point to the target forward
- tip: when looking at the target, the y axis can be above or below the z axis. The second parameter is used here. If it is not filled in, the default is vector Up above. If you want to change direction, you can use vector down
For the same scene, we use quaternion Lookrotation() to make the target face the target direction and the code on the target
//Find the target direction
Vector3 targetDir = m_TargetTran.position - m_MainTran.position;
//Calculate the rotation quaternion required for the z-axis towards the target direction
Quaternion rotation = Quaternion.LookRotation(targetDir,Vector3.up);
//Let m_MainTran.rotation is equal to the calculated rotation
m_MainTran.rotation = rotation;
design sketch
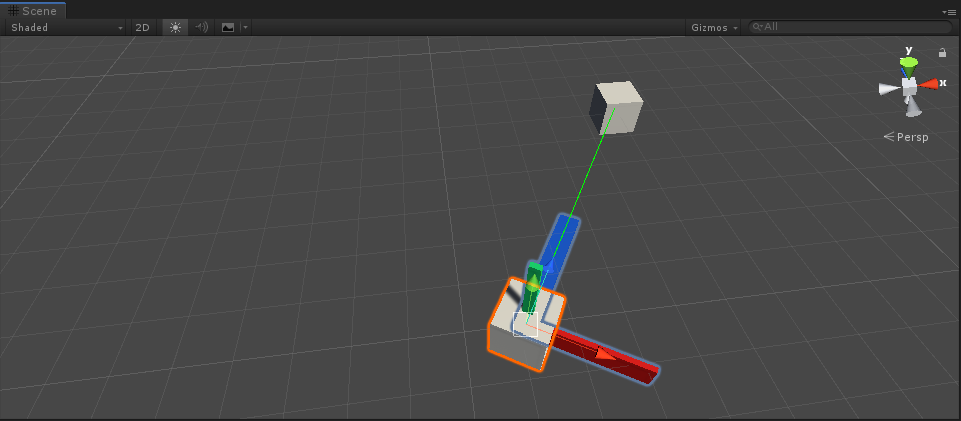
It can be seen that the main object also successfully faces the target. The rotation obtained by this method represents the rotation required for the Z-axis towards the target direction. What if we want the X-axis to face the target direction.
- You can make your right equal to your forward after you get the result. Such as the following code
Vector3 targetDir = m_TargetTran.position - m_MainTran.position;
Quaternion rotation = Quaternion.LookRotation(targetDir,Vector3.up);
m_MainTran.rotation = rotation;
//The above code will make the z-axis towards the target. On this basis, let right face forward
m_MainTran.right = m_MainTran.forward;
design sketch
2, Rotation interpolation and animation implementation
Quaternion.Lerp(Quaternion a, Quaternion b, float t)
- Officials between a and B by T and normalizes the result after The parameter t is clamped to the range [0, 1]
- Interpolation between quaternions a and b, interpolation range t = [0 ~ 1]
We can use quaternion Lerp() to realize the rotation animation. Note that the parameters filled in here are quaternions. We can use quaternion Fromtorotation() or quaternion Lookrotation() to find the parameters we want.
Next, let's realize that the Z axis of the main target turns to the target direction in 2 seconds
private bool isRotating = false;
private float curTime = 0;
private float AllTime = 3;
private Quaternion oldQ;
private Quaternion targetQ;
// Update is called once per frame
void Update()
{
if (Input.GetKeyDown(KeyCode.A))
{
isRotating = true;
curTime = 0;
//Current rotation
oldQ = m_MainTran.rotation;
//Target rotation
targetQ = Quaternion.LookRotation(m_TargetTran.position - m_MainTran.position);
}
if (isRotating)
{
curTime += Time.deltaTime;
float t = curTime / AllTime;
t = Mathf.Clamp(t, 0, 1);
//Interpolation with t
Quaternion lerpQ = Quaternion.Lerp(oldQ,targetQ,t);
//Set to target rotation
m_MainTran.rotation = lerpQ;
Debug.Log($"{GetType()} curT:{t}");
if (t >= 1)
{
isRotating = false;
}
}
}
design sketch
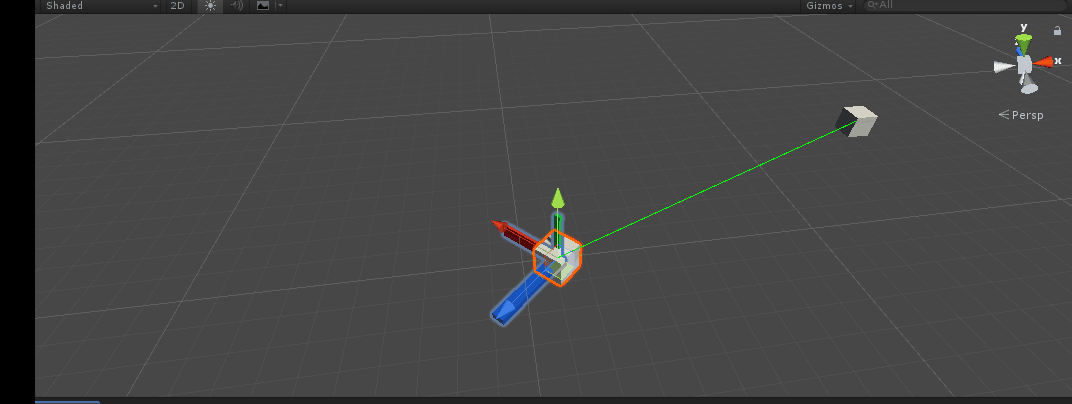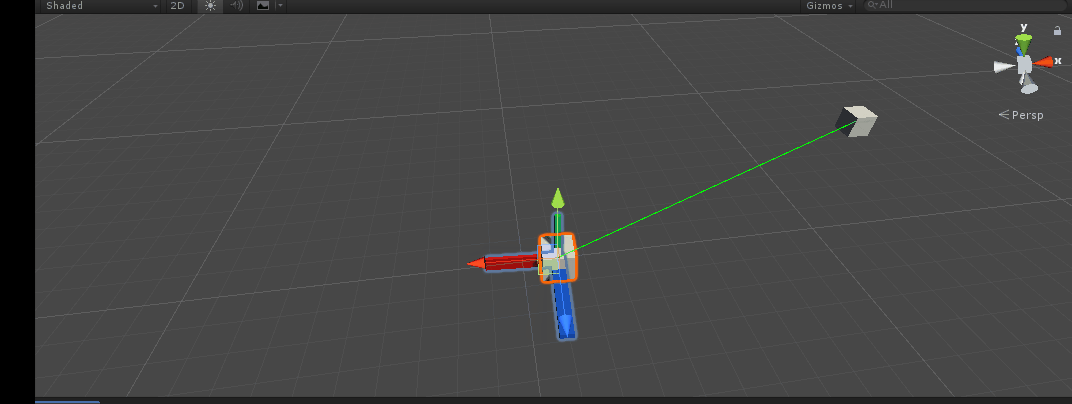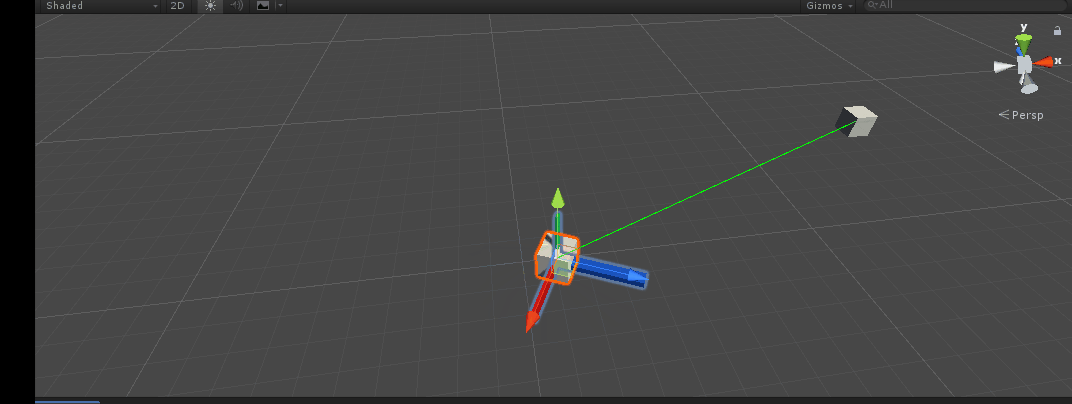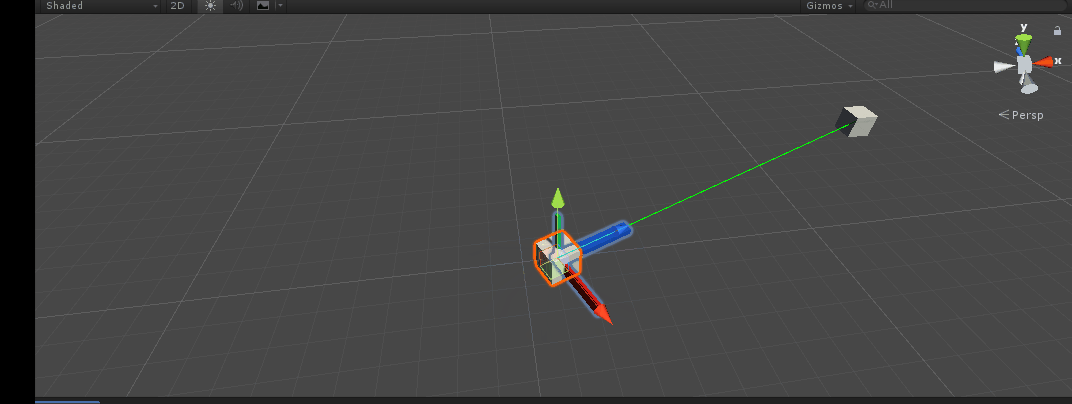
Sometimes what we need is other axes, such as X-axis facing the target. What should we do. Next, let's implement the code
private bool isRotating = false;
private float curTime = 0;
private float AllTime = 3;
private Vector3 oldDir;
private Quaternion oldQ;
private Quaternion targetQ;
// Update is called once per frame
void Update()
{
if (Input.GetKeyDown(KeyCode.A))
{
isRotating = true;
curTime = 0;
//Record the orientation of the starting point
oldDir = m_MainTran.right;
//Initial interpolation parameter (for the oldDir direction, the initial does not need to be rotated, so here is Quaternion.identity)
oldQ = Quaternion.identity;
//Target interpolation parameters
targetQ = Quaternion.FromToRotation(m_MainTran.right, m_TargetTran.position - m_MainTran.position);
}
if (isRotating)
{
curTime += Time.deltaTime;
float t = curTime / AllTime;
t = Mathf.Clamp(t, 0, 1);
//Interpolation with t
Quaternion lerpQ = Quaternion.Lerp(oldQ,targetQ,t);
//Set to target rotation
m_MainTran.right = lerpQ * oldDir;
Debug.Log($"{GetType()} curT:{t}");
if (t >= 1)
{
isRotating = false;
}
}
}
design sketch:
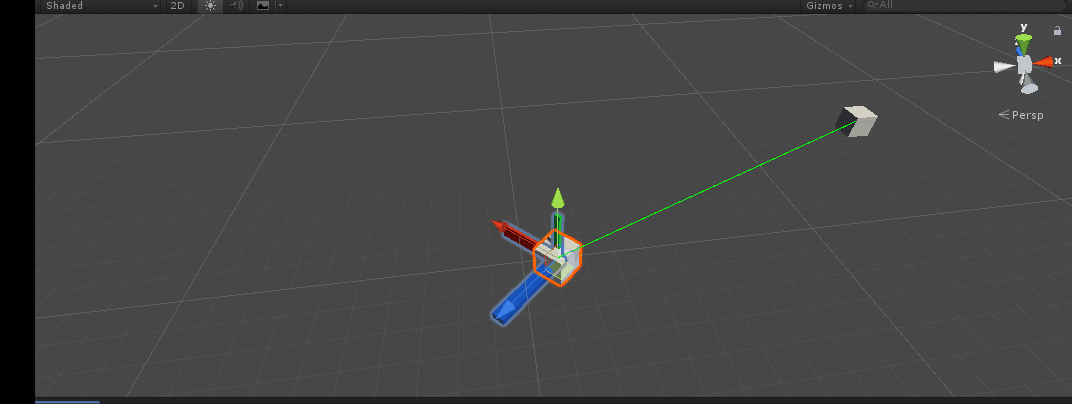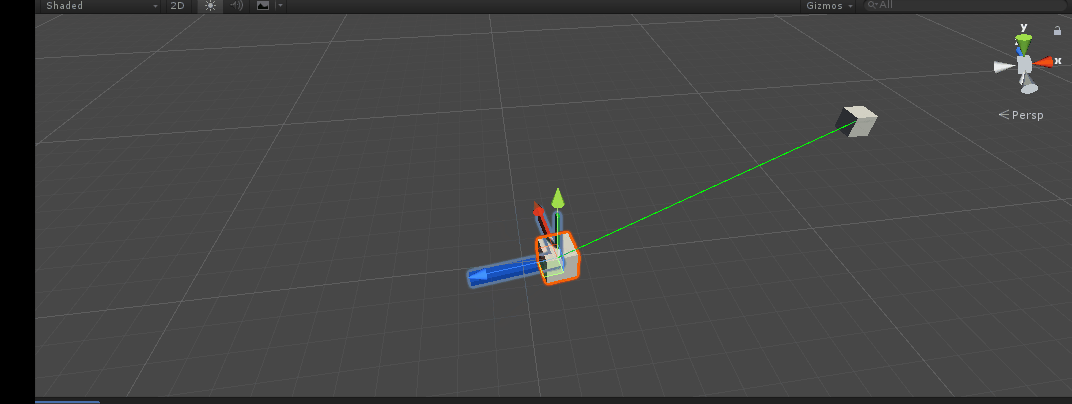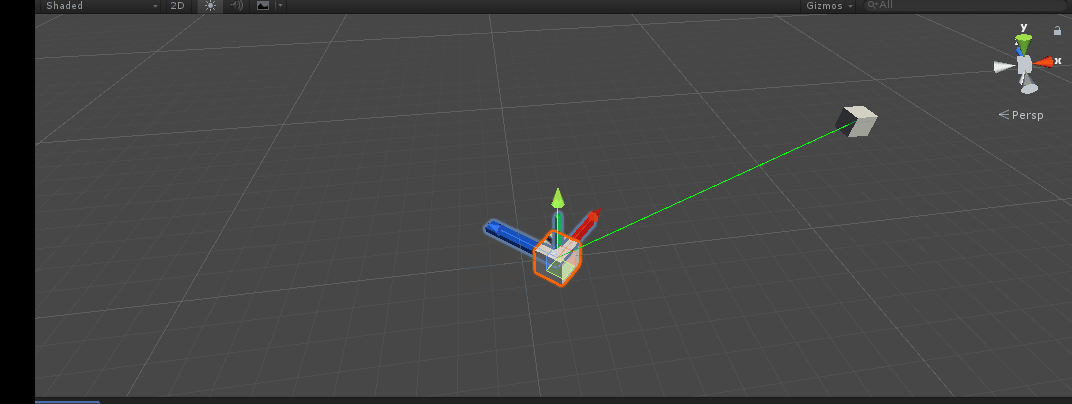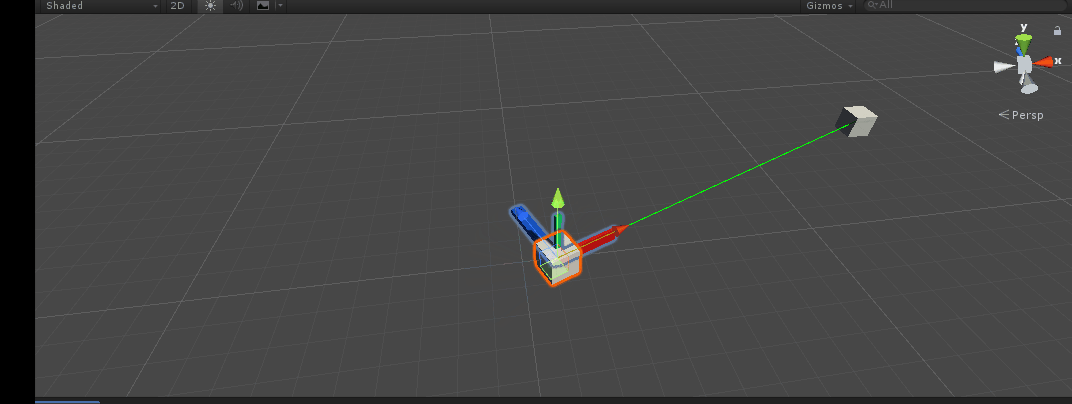Comments are added to the code. Press the A key and you can see that our X-axis has turned to the target
Quaternion.Slerp(Quaternion a, Quaternion b, float t)
This is spherical interpolation, and the animation effect may be better than quaternion LERP () is better.
Specific usage and quaternion Like Lerp(), you only need to change Lerp() in the above code to Slerp() to see the effect. It's not listed here. You can replace it yourself.
Quaternion.RotateTowards(Quaternion from,Quaternion to,float maxDegreesDelta)
- Official analysis: rotates a rotation from directions to
- Turn the rotation from from to. The rotation angle is maxDegreesDelta, but the final rotation will not exceed to So this is the theoretical maximum rotation angle.
You can see the source code. In fact, quaternion is also used here Slerpunclamped(). First find the total angle, and then
maxDegreesDelta / total angle as interpolation t
public static Quaternion RotateTowards(
Quaternion from,
Quaternion to,
float maxDegreesDelta)
{
float num = Quaternion.Angle(from, to);
return (double) num == 0.0 ? to : Quaternion.SlerpUnclamped(from, to, Mathf.Min(1f, maxDegreesDelta / num));
}
With this method, we can specify the rotation angle to turn to the target. Next, let's try the code
private bool isRotating = false;
private float perAngel = 15;//15 degrees per second
private Quaternion targetQ;
// Update is called once per frame
void Update()
{
if (Input.GetKeyDown(KeyCode.A))
{
isRotating = true;
curTime = 0;
//Target interpolation parameters
targetQ = Quaternion.LookRotation(m_TargetTran.position - m_MainTran.position);
}
if (isRotating)
{
//Calculate the rotation of each frame
Quaternion rotQ = Quaternion.RotateTowards(transform.rotation,targetQ,perAngel * Time.deltaTime);
//Set to target rotation
m_MainTran.rotation = rotQ;
if (m_MainTran.rotation.Equals(targetQ))
{
isRotating = false;
Debug.Log($"{GetType()} exit rot");
}
}
}
design sketch:
Quaternion AngleAxis(float angle, Vector3 axis)
-
Official analysis: Creates a rotation which rotates angle degrees around axis
-
Create a rotation. Represents the angle of rotation with the axis direction as the rotation axis
-
In this way, we can rotate our direction along any axis at any angle, and accurately rotate according to the effect we want.
For example, in 2D games, we usually follow the vector Forward to rotate;
In 3D space, which direction should we rotate?
We can use the fork to multiply the rotation. Mathematical meaning of cross multiplication: vector c = vector3 Cross(a,b); The calculated vector c is perpendicular to the plane formed by vectors a and B. We can use c as the axis of rotation.
Next, we use quaternion Angleaxis() to achieve the previous rotation animation. Upper code
private bool isRotating = false;
private float perAngel = 15;//15 degrees per second
private Vector3 rotAxis;
// Update is called once per frame
void Update()
{
if (Input.GetKeyDown(KeyCode.A))
{
isRotating = true;
//Find the rotation axis
rotAxis = Vector3.Cross(m_MainTran.forward,m_TargetTran.position - m_MainTran.position);
}
if (isRotating)
{
//Calculate the rotation of each frame
Quaternion rotQ = Quaternion.AngleAxis(perAngel * Time.deltaTime,rotAxis);
//Apply rotation
m_MainTran.forward = rotQ * m_MainTran.forward;
//If the rotation is only 2 degrees away, it rotates to the target direction and exits the rotation animation
if (Vector3.Angle(m_MainTran.forward,m_TargetTran.position - m_MainTran.position) <= 2)
{
m_MainTran.forward = m_TargetTran.position - m_MainTran.position;
isRotating = false;
Debug.Log($"{GetType()} exit rot");
}
}
}
design sketch:
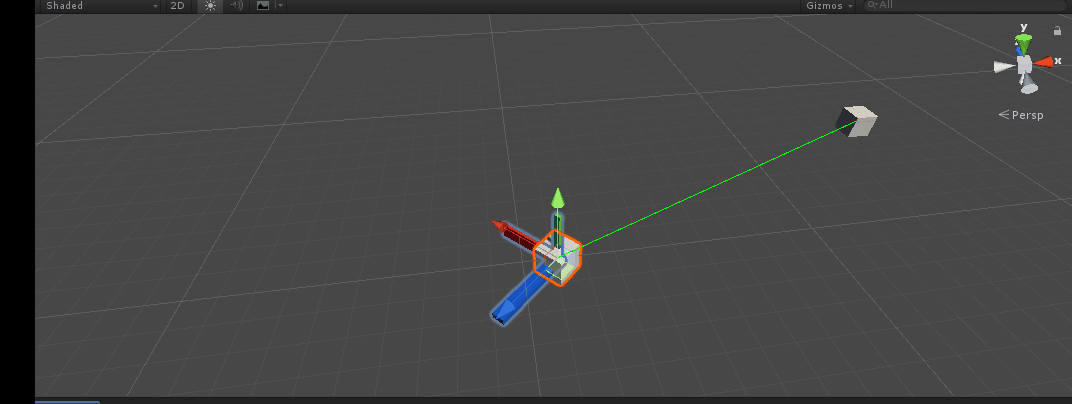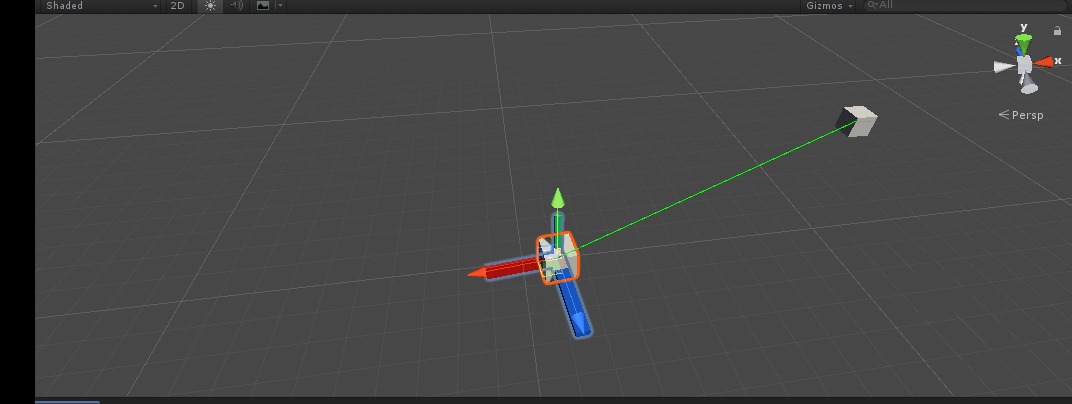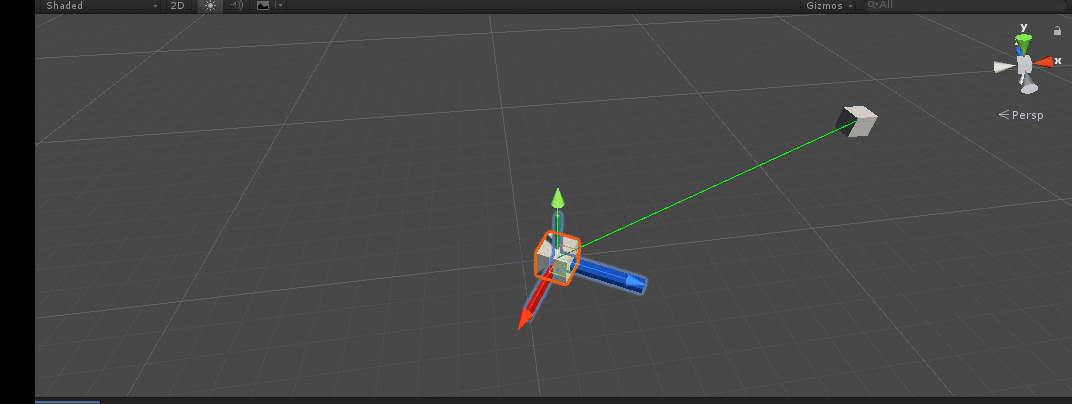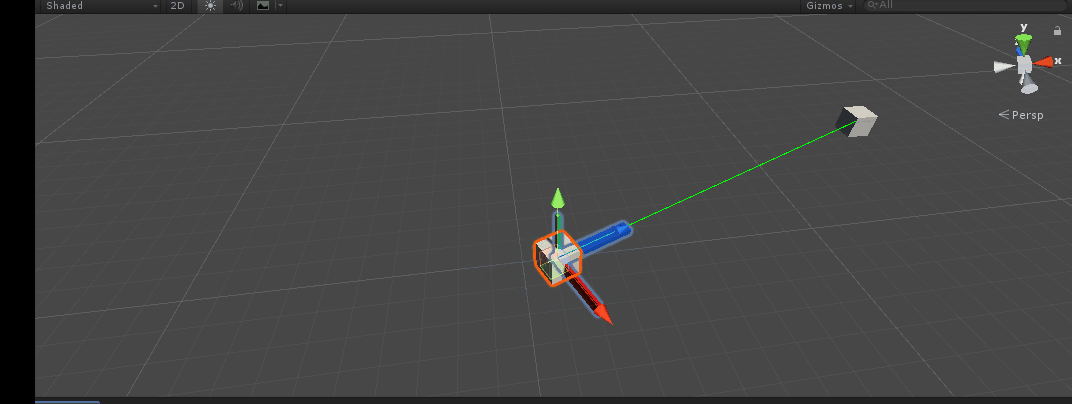
It can be seen that the main object has also successfully turned to the target. Quaternion is a relatively abstract concept, but if you master the above API, you can turn around as you like~