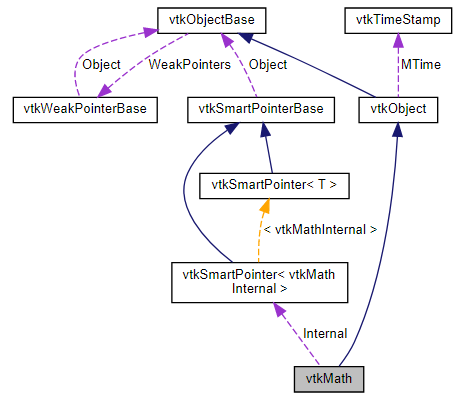
vtkMath
vtkMath provides a way to perform common mathematical operations. These include providing constants, such as Pi; Conversion from degrees to radians; Vector operations, such as dot product, cross product and vector norm; Matrix determinants of 2x2 and 3x3 matrices; Univariate polynomial solver; For random number generation (backward compatibility only).
Constant definition
Define commonly used PI:
static constexpr double Pi() { return 3.141592653589793; }
The PI value calculated by cos(-1) is 3.1415926535897931;
Basic data operation
rounding
static int Round(float f) { return static_cast<int>(f + (f >= 0.0 ? 0.5 : -0.5)); }
static int Round(double f) { return static_cast<int>(f + (f >= 0.0 ? 0.5 : -0.5)); }
double type to other type conversion
In the calculation, it is often encountered that the value of double type is assigned to other types. If the type conversion is directly enforced, the precision will decline or the value will overflow;
RoundDoubleToIntegralIfNecessary converts the val value to the OutT type value, which can ensure that the ret value is within the reasonable range of the OutT type and will not overflow;
template <typename OutT>
static void RoundDoubleToIntegralIfNecessary(double val, OutT* ret) {
vtk_detail::RoundDoubleToIntegralIfNecessary(val, ret);
}
Interception of integer numbers
Floor is rounded down and Ceil is rounded up;
inline int vtkMath::Floor(double x)
{
int i = static_cast<int>(x);
return i - (i > x);
}
inline int vtkMath::Ceil(double x)
{
int i = static_cast<int>(x);
return i + (i < x);
}
power function
Ceilllog2 gives two exponents that are not less than the minimum power of x.
static int CeilLog2(vtkTypeUInt64 x);
The ispoweoftwo function returns true if the integer is a power of 2.
inline bool vtkMath::IsPowerOfTwo(vtkTypeUInt64 x){
return ((x != 0) & ((x & (x - 1)) == 0));
}
The NearestPowerOfTwo function is used to calculate two nearest powers not less than x.
If x is less than or equal to zero, the return value is 1; If the result is too large to be put into an integer, the return value is VTK_INT_MIN.
inline int vtkMath::NearestPowerOfTwo(int x){
unsigned int z = static_cast<unsigned int>(((x > 0) ? x - 1 : 0));
z |= z >> 1;
z |= z >> 2;
z |= z >> 4;
z |= z >> 8;
z |= z >> 16;
return static_cast<int>(z + 1);
}
Factorial is used to calculate N factorial;
static vtkTypeInt64 Factorial(int N);
random number
There are notes in VTK: do not use Random(), RandomSeed(), GetSeed(), Gaussian(). This is static, so it is prone to errors (especially for regression testing), which is just for backward compatibility.
static void RandomSeed(int s); static int GetSeed(); static double Random(); static double Random(double min, double max); // Generate pseudo-random numbers distributed according to standard normal distribution. static double Gaussian(); static double Gaussian(double mean, double std);
Sampling and random array
Binomial the number of combinations of n objects from the m object (M > n) pool.
static vtkTypeInt64 Binomial(int m, int n);
BeginCombination function function: start iteration of "m selects n" object and return an array of N integers, each integer from 0 to m-1. These integers represent n items selected from the set [0, M]. Once the iterator is no longer needed, you need to call vtkMath::FreeCombination().
NextCombination gives a valid combination of N integers in the range of m, N and [0, m]. This function changes the integer to the next combination in all combination sequences of n items in m pools. If the combination is the last item in the sequence at input, the combination remains unchanged and returns 0. Otherwise, 1 is returned and the combination is updated.
FreeCombination function function: release the combination pointer generated by BeginCombination;
static int* BeginCombination(int m, int n); static int NextCombination(int m, int n, int* combination); static void FreeCombination(int* combination);
Max min
template <class T> static T Min(const T& a, const T& b); template <class T> static T Max(const T& a, const T& b);
assignment
template <class VectorT1, class VectorT2>
static void Assign(const VectorT1& a, VectorT2&& b){
b[0] = a[0];
b[1] = a[1];
b[2] = a[2];
}
static void Assign(const double a[3], double b[3]) { vtkMath::Assign<>(a, b); }
addition
Addition calculation of float array and double array;
static void Add(const float a[3], const float b[3], float c[3]){
for (int i = 0; i < 3; ++i)
{
c[i] = a[i] + b[i];
}
}
static void Add(const double a[3], const double b[3], double c[3]){
for (int i = 0; i < 3; ++i)
{
c[i] = a[i] + b[i];
}
}
subtraction
Subtraction between arrays and vectors;
static void Subtract(const float a[3], const float b[3], float c[3]) {
for (int i = 0; i < 3; ++i) {
c[i] = a[i] - b[i];
}
}
static void Subtract(const double a[3], const double b[3], double c[3]) {
for (int i = 0; i < 3; ++i) {
c[i] = a[i] - b[i];
}
}
template <class VectorT1, class VectorT2, class VectorT3>
static void Subtract(const VectorT1& a, const VectorT2& b, VectorT3&& c) {
c[0] = a[0] - b[0];
c[1] = a[1] - b[1];
c[2] = a[2] - b[2];
}
multiplication
MultiplyScalar * is used to calculate the multiplication of array and factor s;
static void MultiplyScalar(float a[3], float s) {
for (int i = 0; i < 3; ++i) {
a[i] *= s;
}
}
static void MultiplyScalar2D(float a[2], float s) {
for (int i = 0; i < 2; ++i) {
a[i] *= s;
}
}
static void MultiplyScalar(double a[3], double s) {
for (int i = 0; i < 3; ++i) {
a[i] *= s;
}
}
static void MultiplyScalar2D(double a[2], double s) {
for (int i = 0; i < 2; ++i) {
a[i] *= s;
}
}
Angle and radian
The commonly used calculation of angle Radian and Radian Degree is the conversion from angle to Radian, using Pi value;
double ratio = 3.1415926 / 180; double aratio = 180 / 3.1415926;
In VTK, PI/180 is defined as constant 0.017453292519943295, and 180.0/PI is defined as constant 57.29577951308232;
inline float vtkMath::RadiansFromDegrees(float x){
return x * 0.017453292f;
}
inline double vtkMath::RadiansFromDegrees(double x){
return x * 0.017453292519943295;
}
inline float vtkMath::DegreesFromRadians(float x){
return x * 57.2957795131f;
}
inline double vtkMath::DegreesFromRadians(double x){
return x * 57.29577951308232;
}
Vector operation
Dot product
Dot product operation of two vectors, supporting float type and double type;
static float Dot(const float a[3], const float b[3]) {
return a[0] * b[0] + a[1] * b[1] + a[2] * b[2];
}
static double Dot(const double a[3], const double b[3]) {
return a[0] * b[0] + a[1] * b[1] + a[2] * b[2];
}
template <typename ReturnTypeT = double, typename TupleRangeT1, typename TupleRangeT2,
typename EnableT = typename std::conditional<!std::is_pointer<TupleRangeT1>::value &&
!std::is_array<TupleRangeT1>::value, TupleRangeT1, TupleRangeT2>::type::value_type>
static ReturnTypeT Dot(const TupleRangeT1& a, const TupleRangeT2& b) {
return a[0] * b[0] + a[1] * b[1] + a[2] * b[2];
}
Cross product
// Cross product of two 3-vectors. Result (a x b) is stored in c[3].
inline void vtkMath::Cross(const float a[3], const float b[3], float c[3]) {
float Cx = a[1] * b[2] - a[2] * b[1];
float Cy = a[2] * b[0] - a[0] * b[2];
float Cz = a[0] * b[1] - a[1] * b[0];
c[0] = Cx;
c[1] = Cy;
c[2] = Cz;
}
// Cross product of two 3-vectors. Result (a x b) is stored in c[3].
inline void vtkMath::Cross(const double a[3], const double b[3], double c[3]) {
double Cx = a[1] * b[2] - a[2] * b[1];
double Cy = a[2] * b[0] - a[0] * b[2];
double Cz = a[0] * b[1] - a[1] * b[0];
c[0] = Cx;
c[1] = Cy;
c[2] = Cz;
}
External product
Calculates the outer product (floating point) of two 3 vectors.
static void Outer(const float a[3], const float b[3], float c[3][3]){
for (int i = 0; i < 3; ++i){
for (int j = 0; j < 3; ++j){
c[i][j] = a[i] * b[j];
}
}
}
static void Outer(const double a[3], const double b[3], double c[3][3]){
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 3; ++j) {
c[i][j] = a[i] * b[j];
}
}
}